8.2: Appendix 1 - Electron Wavepacket Propagation
- Page ID
- 52429
Stationary states and eigenfunctions
Until now, we have not considered the velocity of electrons because we have not considered the time dependence of solutions to the Schrödinger equation. In Part 1, we broke the full Schrödinger Equation into two coupled equations: an equation in time, and another in space. The separation is possible when the potential energy is constant in time. Then the spatial and time dependencies of the solution can be separated, i.e.
\[ \Psi(x,t)=\psi(x)\zeta(t) \label{8.2.1} \]
The time dependence is described by:
\[ E\zeta(t)=i \hbar \frac{d}{dt}\zeta(t) \label{8.2.2} \]
and the spatial dependence is given by
\[ E\psi(x)= -\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\psi(x)+V(x)\psi(x) \label{8.2.3}. \]
Solutions to these coupled equations are characterized by a time-independent probability density. The general solution to Equation \ref{8.2.2} is
\[ \zeta(t) = \zeta(0)\exp\left[ -i\frac{E}{\hbar}t \right] \label{8.2.4} \]
and the probability density is:
\[ |\Psi(x,t)|^{2} = |\psi(x)\zeta(t)|^{2}=|\psi(x)|^{2}|\zeta(0)|^{2} \label{8.2.5} \]
Because the solution does not evolve with time, it is said to be "stationary". These solutions are important and are known as "eigenfunctions". Eigenfunctions are extremely important in quantum mechanics. You can think of them as the natural functions for a particular system. Each eigenfunction is associated with a constant, known as the eigenvalue: in this case the constant energy, E.
An arbitrary wavefunction, however, will not necessarily be an eigenfunction or stationary. For example, consider a wavefunction constructed from two eigenfunctions:
\[ | \psi(x)\rangle = a_{1}|\psi_{1}(x)\rangle + a_{2}|\psi_{2}(x)\rangle \label{8.2.6} \]
where a and b are constants. This is known as a linear combination of eigenfunctions. The full solution is
\[ \Psi(x,t) = a_{1}\psi_{1}(x)e^{-i\frac{E_{1}}{\hbar}t} + a_{2}\psi_{2}(x)e^{-i\frac{E_{2}}{\hbar}t} \label{8.2.7} \]
Substituting into the Schrödinger Equation gives
\[ H|a_{1}\psi_{1}(x)e^{-i\frac{E_{1}}{\hbar}t} + a_{2}\psi_{2}(x)e^{-i\frac{E_{2}}{\hbar}t}\big\rangle =a_{1}E_{1}|\psi_{1}(x)e^{-i\frac{E_{1}}{\hbar}t}\big\rangle + a_{2}E_{2}|\psi_{2}(x)e^{-i\frac{E_{2}}{\hbar}t}\big\rangle \label{8.2.8} \]
i.e., the linear combination is not necessarily itself an eigenfunction. It is not stationary: the phase of each eigenfunction component evolves at a different rate. The probability density shows time dependent interference between each rotating phase term. For example, assuming that \(a_{1}\), \(a_{2}\), \(\psi_{1}\) and \(\psi_{2}\) are real:
\[ |\Psi{x,t}|^{2} = a_{1}^{2}\psi_{1}^{2}(x)+a_{2}^{2}\psi_{2}^{2}(x)+2a_{1}\psi_{1}(x)\psi_{2}(x) cos\left(\left( E_{2}-E_{1} \right) \frac{t}{\hbar}\right) \label{8.2.9}. \]
Completeness
We will not prove completeness in the class. Instead we merely state that the completeness property of eigenfunctions allows us to express any well-behaved function in terms of a linear combination of eigenfunctions. i.e. if \(|\phi_{n}\rangle\) is an eigenfunction, then an arbitrary well-behaved wavefunction can be written
\[ |\psi\rangle = \sum_{n}a_{n}|\phi_{n}\big\rangle \label{8.2.10} \]
Completeness also requires that the potential be finite within the region of interest. For example, no combination of eigenfunctions of the infinite square well can ever describe a non-zero wavefunction amplitude at the walls.
Re-expressing the wavefunction in terms of a weighted sum of eigenfunctions is a little like doing a Fourier transform, except that instead of re-expressing the wavefunction in terms of a linear combination of exp[ikx] factors, we are using the eigenfunctions.\(^{†}\)
The problem now is the determination of the weighting constants, \(a_{n}\).
For this we need the next property of eigenfunctions:
Orthogonality
Eigenfunctions with different eigenvalues are orthogonal. i.e. the bracket of eigenfunctions corresponding to different eigenvalues is zero:
\[ \left< \phi_{j}|\phi_{i}\right> = 0,\ for\ i \neq j, \ E_{i}\neq E_{j} \label{8.2.11} \]
If different eigenfunctions have identical eigenvalues (i.e. same energy) they are known as degenerate.
Calculation of coefficients
Starting from Equation \ref{8.2.10} we have
\[ |\psi \rangle = \sum_{n}a_{n}|\phi_{n}\big\rangle \label{8.2.12} \]
Now, let's take the bracket with an eigenfunction \(\big\langle\phi_{k}|\)
\[ \left< \phi_{k}|\psi \right> =\left< \phi_{k} |\sum_{n}a_{n}|\phi_{n} \right> = \sum_{n}a_{n}\left< \phi_{k}|\phi_{n} \right> \label{8.2.13} \]
From the statement of orthogonality in Equation \ref{8.2.11} we have
\[ \left< \phi_{k}|\phi_{n} \right> = \delta_{nk} \label{8.2.14} \]
where \(\delta_{nk}\) is the Kronecker delta function, i.e. \(\delta_{nk}=1\) only when n = k.
Thus,
\[ a_{k}=\left< \phi_{k}|\psi \right> \label{8.2.15}. \]
These coefficients are very important.
Since the eigenfunctions are usually known, often the set of coefficients provides the interesting information in a particular problem. This may be clear from an example.
An example: the expanding square well
Consider an electron occupying the ground state of an infinite square well of length L. As shown in Figure \(\PageIndex{1}\), at time t = 0, the well suddenly triples in size. What happens to the electron?
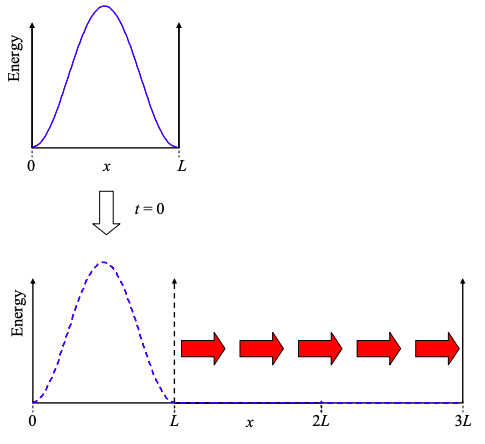
Let's begin to answer this question by considering the wavefunction prior to the expansion of the well:\(^{†}\)
\[ \psi(x)=\sqrt{\frac{2}{L}}\sin(\pi x/L),\ 0\leq x\leq L \label{8.2.16} \]
If we substitute this back into the Schrödinger Equation we can easily confirm that the effect of operating on this wavefunction with the Hamiltonian is the same as multiplying the wavefunction by a constant. i.e.
\[ H \bigg|\sqrt{\frac{2}{L}}\sin(\pi x/L) \bigg \rangle = E\bigg|\sqrt{\frac{2}{L}}\sin(\pi x/L) \bigg \rangle \label{8.2.17} \]
Thus, this wavefunction is an eigenfunction of the original square well, and the constant, E, the energy, is the eigenvalue corresponding to the eigenfunction.
Now, Equation \ref{8.2.16} is the lowest energy eigenfunction for the time independent infinite square well potential. The wavefunction evolves in time according to
\[ E\zeta(t)=i\hbar \frac{d}{dt}\zeta(t) \label{8.2.18} \]
Solving Equation \ref{8.2.2} gives:
\[ \Psi(x,t) = \psi(x)\zeta(t) = \sqrt{\frac{2}{L}} \sin(\pi x/L)\exp\left[-i \frac{E}{\hbar}t\right] \label{8.2.19} \]
where
\[ E =E_{L} = \frac{\hbar^{2}\pi^{2}}{2mL^{2}} \label{8.2.20} \]
The probability density, however, is time independent:
\[ |\Psi(x,t)|^{2} =\frac{2}{L}\sin^{2}(\pi x/L),\ 0 \leq x \leq L \label{8.2.21} \]
We have verified that the eigenfunction is stationary, as it must be.
Now, when the well expands, the wavefunction cannot change instantaneously. To confirm this, consider a step change in the wavefunction in Equation \ref{8.2.2} – the energy would tend to \(\infty\).
But the stationary states of the new well are
\[ \psi(x) = \sqrt{\frac{2}{3L}}\sin(n\pi x /3L), \ \ 0\leq x\leq 3L \label{8.2.22} \]
i.e. the wavefunction of the electron at t = 0 is not a stationary state in the expanded well. To determine the evolution of the electron wavefunction in time, we must re-express the wavefunction in terms of the eigenfunctions of the expanded well. We can then calculate the evolution of each eigenfunction from Equation \ref{8.2.2}.
The wavefunction is now described as a linear combination of eigenfunctions:
\[ \psi(x) = \sqrt{\frac{2}{L}}\sin(n\pi x /L), \ \ 0\leq x\leq L \\
= \sum_{n} a_{n} \sqrt{\frac{2}{3L}}\sin(n\pi x /3L), \ \ 0\leq x\leq 3L \label{8.2.23} \]
where \(a_{n}\) is a set of constants, that weight the contributions from each eigenfunction.
We express the wavefunction as a linear combination of the eigenfunctions of the expanded well. From Equation \ref{8.2.15} we have
\[ \psi(x) = \sum_{n} a_{n} \sqrt{\frac{2}{3L}}\sin(n\pi x /3L), \ \ 0\leq x\leq 3L \label{8.2.24} \]
Thus, the coefficients are
\[ a_{n} = \left< \phi_{n}|\psi \right> = \int^{L}_{0} \sqrt{\frac{2}{3}} \sin(\pi x/L) \sqrt{\frac{2}{3L}} \sin(n \pi x/3L)dx \label{8.2.25} \]
Solving gives
\[ a_{n} =
\begin{cases}
\frac{1}{\sqrt{3}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n=3 \\
-\frac{6\sqrt{3}}{\pi} \frac{\sin(n\pi/3)}{n^{2}-9} \ \ \ \ n \neq 3
\end{cases} \label{8.2.26} \]
In Figure \(\PageIndex{2}\) we plot the cumulative effect of adding the weighted eigenfunctions. After about 10 eigenfunctions, the linear combination is a close approximation to the initial wavefunction.
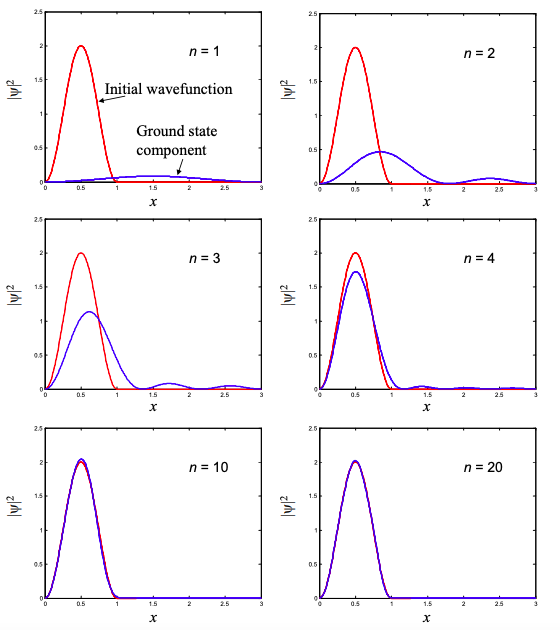
Next, we calculate the evolution of the wavefunction. From Equation \ref{8.2.24}, we get
\[ \Psi(x,t) = \sum_{n} a_{n} \sqrt{\frac{2}{3L}}\sin(n \pi x/3L) \exp\left[-i \frac{E_{n}}{\hbar}t \right], \ \ \ 0 \leq x \leq 3L \label{8.2.27} \]
where
\[ E_{n} = \frac{n^{2} \pi^{2} \hbar^{2}}{2m(3L)^{2}} \label{8.2.28} \]
The evolution of the wavefunction with time is shown in Figure \(\PageIndex{3}\), below.
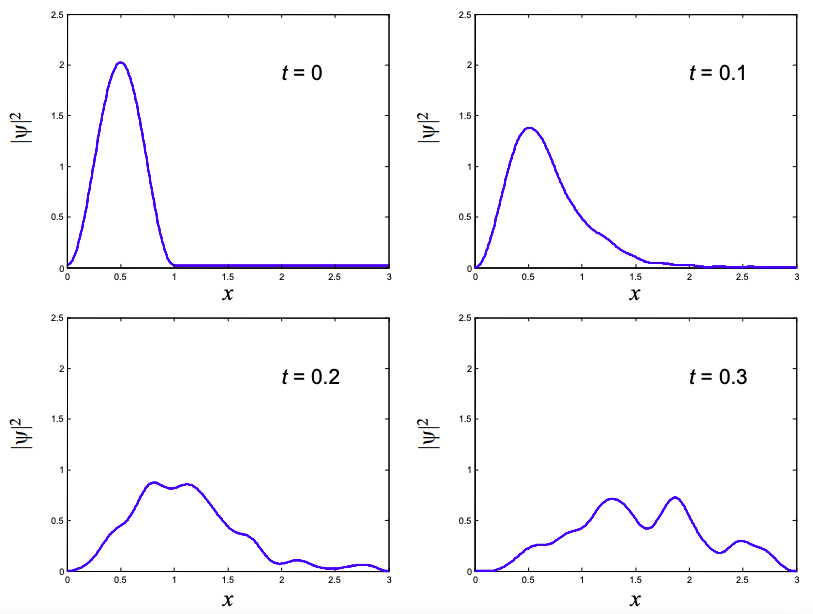
Propagation of a Gaussian Wavepacket
Next we will examine the propagation of a Gaussian wavepacket in free space. Again, we will expand the wavefunction in terms of its eigenfunctions.
Consider an electron in free space. Let the initial wavepacket be a Gaussian.
\[ \psi(x,0) = (\pi L^{2})^{-1/4} \exp \left[ ik_{0}x \right] \label{8.2.29} \]
Note that we have introduced a phase factor \(\exp \left[ ik_{0}x \right]\). Recall that multiplying the real space wavefunction by the phase factor \(\exp \left[ ik_{0}x \right]\), is equivalent to shifting the k-space wavefunction by \(k_{0}\). Since the Fourier transform was centered at k = 0 prior to the shift, the phase factor shifts the expectation value of k to \(k_{0}\). Hence the factor \(\exp \left[ ik_{0}x \right]\) gives the wavepacket has a non-zero average momentum.
Now, the eigenfunctions of the Schrödinger Equation in free space are the complex exponentials
\[ \phi(k)= \exp[ikx] \label{8.2.30} \]
where k is continuous.
Each eigenfunction evolves with time as
\[ \phi(k,t)= \exp[ikx]\exp\left[ -i\frac{E}{\hbar}t \right] \label{8.2.31} \]
Expanding the wavefunction as a linear combination of these eigenfunctions we have
\[ \psi(x,t)=\frac{1}{2\pi}\int^{+\infty}_{-\infty} A(k) \phi(k,t)dk \label{8.2.32} \]
\[ \psi(x,t)=\frac{1}{2\pi}\int^{+\infty}_{-\infty} A(k)\exp[ikx]\exp\left[ -i \frac{E}{\hbar} t\right]dk \label{8.2.33} \]
where \(A(k)/2\pi\) describes the weighting of each complex exponential eigenfunction.
Since \(\phi(k) = \exp[ikx]\), Equation \ref{8.2.32} evaluated at t = 0 is simply the inverse Fourier transform:
\[ \psi(x) = \frac{1}{2\pi} \int^{+\infty}_{-\infty} A(k)\exp[ikx] dk \label{8.2.34} \]
Thus, A(k) is determined from the Fourier transform of the wavefunction
\[ A(k) = \left< \phi(k)|\psi(x,0) \right> = \int^{+\infty}_{-\infty} \psi(x,0)e^{-ikx}dx = (4\pi L^{2})^{1/4}\exp \left[ -\frac{L^{2}(k-k_{0})^{2}}{2} \right] \label{8.2.35} \]
Now, before we can substitute A(k) back into Equation \ref{8.2.32} to get the time evolution of \(\psi(x,t)\) we need to consider the possible k dependence of energy, E.
In general the relation between E and k is known as the dispersion relation.
The dispersion relation is important because propagation of an electron in free space, or in a particular material is determined by the dispersion relation. Let's consider some examples.
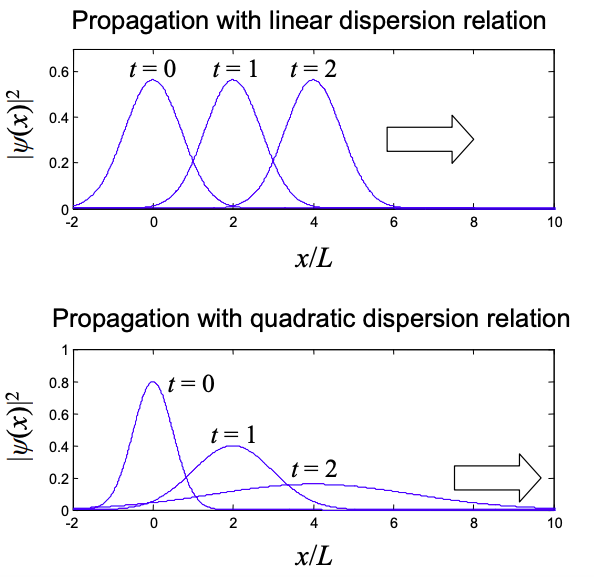
Linear dispersion relation
The dispersion relation determines how the wavepacket spreads in time. For example, if instead of an electron we were considering a photon with \(E = \hbar\omega = \hbar c k\), the dispersion relation is linear and the photon does not spread as it propagates.
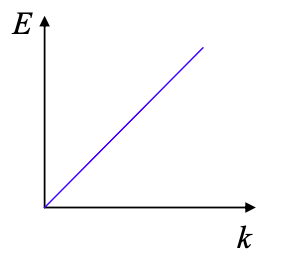
The time dependent factor is
\[ \exp\left[ -i \frac{E}{\hbar}t \right] \equiv \exp[-i\omega t] = \exp \left[ -ickt \right] \label{8.2.36}. \]
Solving Equation \ref{8.2.32} gives
\[ \psi(x,t) = \frac{1}{(\pi L^{2})^{1/2}}\exp\left[ -\frac{(x-ct)^{2}}{L^{2}} \right] \label{8.2.37} \]
Thus, the probability density is simply the original function shifted linearly in time:
\[ |\psi(x,t)|^{2} = \frac{1}{(\pi L^{2})^{1/2}}\exp\left[ -\frac{(x-ct)^{2}}{L^{2}} \right] \label{8.2.38} \]
Quadratic dispersion relation
For plane wave eigenfunctions, however, the dispersion relation is quadratic and we have
\[ E = \frac{\hbar^{2}k^{2}}{2m} \label{8.2.39} \]

As we have seen, particles in a box also have quadratic dispersion relations.
Thus the time dependent factor is
\[ \exp \left[ -i\frac{E}{\hbar} t\right] \equiv \exp[-i\omega t] \exp\left[ -i \frac{\hbar k^{2}}{2m}t \right] \label{8.2.40} \]
Solving Equation \ref{8.2.32} gives
\[ \psi(x,t) = \frac{1}{(\pi L^{2})^{1/4}} \frac{1}{\sqrt{1+i\hbar t/mL^{2}}} \exp\left[ i\left(k_{0}x-\frac{\hbar k_{0}^{2}t}{2m} \right) \right]\exp\left[- \frac{(x-\hbar k_{0}t/m)^{2}}{2L^{2}(1+i\hbar t/mL^{2})} \right] \label{8.2.41} \]
and
\[ |\psi(x,t)|^{2}=\left(2\pi [\Delta x(t)]^{2} \right)^{-1/2} \exp \left[ -\frac{(x-\hbar k_{0}t/m)^{2}}{2[Delta x(t)]^{2}} \right] \label{8.2.42} \]
where
\[ [\Delta x(t)]^{2}=\frac{L^{2}}{2}\left( 1+\left( \frac{\hbar t}{mL^{2}}\right)^{2} \right) \label{8.2.43} \]
Group Velocity
As with a classical wave, the average velocity of the wavepacket is the group velocity, defined as the time derivative of the expectation value of position:
\[ v_{g}=\frac{d}{dt}\langle x \rangle = \left< \frac{1}{\hbar} \frac{dE}{dk}\right> = \left< \frac{d\omega}{dk} \right> \label{8.2.44} \]
If the wavepacket is highly peaked in k-space it is possible to simplify Equation \ref{8.2.44} by evaluating \(d\omega/dk\) at the expectation value of k:
\[ v_{g} = \left< \frac{d\omega}{dk} \right> \approx \frac{d\omega}{dk} \biggr \rvert_{\left< k\right>} \label{8.2.45} \]
For the linear dispersion relation, \(d\omega/dk\) is constant so we don't need the approximation:
\[ v_{g} = \left< \frac{d\omega}{dk} \right> = \left< \frac{\hbar k}{m} \right> = \frac{\hbar k_{0}}{m} \label{8.2.46} \]
Since \(\hbar k_{0}\) is the expectation value of momentum, this is indeed the average velocity.
Problems
1. Consider the electron in the expanded well discussed in the notes. Numerically simulate the wave function as a function of time. Using the simulation or otherwise, determine the expectation value of energy before and after the well expands? Predict the behavior of the expectation values of position and momentum as a function of time.

2. Consider the wave function in an infinite square well of width L illustrated below at time t = 0. How will the wavefunction evolve for t > 0. Will the wave function ever return to its original position? If so, at what time t = T will this occur?

3. Derive the expression for the propagation of a Gaussian wavepacket with the linear dispersion relation \(E = \hbar \omega = \hbar ck\). (Equation \ref{8.2.37})
\(^{†}\)Note that exp[ikx] provides a continuous set of eigenfunctions for unbound states, i.e., the expansion in terms of eigenfunctions is the Fourier transform.
\(^{†}\)Note that relative the previous square well analysis (see Figure 1.28.1) we have shifted the x-axis here such that the left wall is at x = 0.

