2.6: $T$ or Chain Scattering Parameters of Cascaded Two-Port Networks

The $T$ parameters, also known as chain scattering parameters, are a cascadable form of scattering parameters. They are similar to regular $S$ parameters and can be expressed in terms of the $a$ and $b$ root power waves or traveling voltage waves. Two two-port networks, A and B, in cascade are shown in Figure $\PageIndex{1}$. Here $(A)$ and $(B)$ are used as superscripts to distinguish the parameters of each two-port network, but the subscripts $A$ and $B$ are used for matrix quantities. Since

$$\label{eq:1}a_{2}^{(A)}=b_{1}^{(B)}\quad\text{and}\quad b_{2}^{(A)}=a_{1}^{(B)}$$

Figure $\PageIndex{1}$: Two cascaded two-ports.

it is convenient to put the $a$ and $b$ parameters in cascadable form, leading to the following two-port chain matrix or $T$ matrix representation (with respect to Figure 2.4.3):

$$\label{eq:2} \left[\begin{array}{c}{a_{1}}\\{b_{1}}\end{array}\right] =\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]\left[\begin{array}{c}{b_{2}}\\{a_{2}}\end{array}\right]$$

where the $\text{T}$ matrix or chain scattering matrix is

$$\label{eq:3}\mathbf{T}=\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]$$

$\mathbf{T}$ is very similar to the scattering transfer matrix $(\:^{S}\mathbf{T})$ of Section 2.3.7. The only difference is the ordering of the $a$ and $b$ components. You will come across both forms, so be careful that you understand which is being used. Both forms are used for the same function—cascading two-port networks. The relationships between $\mathbf{T}$ and $\mathbf{S}$ are given by

$$\label{eq:4}\mathbf{T}=\left[\begin{array}{cc}{S_{21}^{-1}}&{-S_{21}^{-1}S_{22}}\\{S_{21}^{-1}S_{11}}&{S_{12}-S_{11}S_{21}^{-1}S_{22}}\end{array}\right]$$

$$\label{eq:5}\mathbf{S}=\left[\begin{array}{cc}{T_{21}T_{11}^{-1}}&{T_{22}-T_{21}T_{11}^{-1}T_{12}}\\{T_{11}^{-1}}&{-T_{11}^{-1}T_{12}}\end{array}\right]$$

For a two-port network, using Equations $\eqref{eq:1}$ and $\eqref{eq:2}$,

$$\label{eq:6}\left[\begin{array}{c}{a_{1}^{(A)}}\\{b_{1}^{(A)}}\end{array}\right]=\mathbf{T}_{A}\left[\begin{array}{c}{b_{2}^{(A)}}\\{a_{2}^{(A)}}\end{array}\right]\quad\text{and}\quad\left[\begin{array}{c}{a_{1}^{(B)}}\\{b_{1}^{(B)}}\end{array}\right]=\mathbf{T}_{B}\left[\begin{array}{c}{b_{2}^{(B)}}\\{a_{2}^{(B)}}\end{array}\right]$$

thus

$$\label{eq:7}\left[\begin{array}{c}{a_{1}^{(A)}}\\{b_{1}^{(A)}}\end{array}\right]=\mathbf{T}_{A}\mathbf{T}_{B}\left[\begin{array}{c}{b_{2}^{(B)}}\\{a_{2}^{(B)}}\end{array}\right]$$

For $n$ cascaded two-port networks, Equation $\eqref{eq:7}$ generalizes to

$$\label{eq:8}\left[\begin{array}{c}{a_{1}^{(1)}}\\{b_{1}^{(1)}}\end{array}\right]=\mathbf{T}_{1}\mathbf{T}_{2}\ldots\mathbf{T}_{n}\left[\begin{array}{c}{b_{2}^{(n)}}\\{a_{2}^{(n)}}\end{array}\right]$$

and so the $\mathbf{T}$ matrix of the cascaded network is the matrix product of the $\mathbf{T}$ matrices of the individual two-ports.

Previously, in Section 2.3.7, the scattering transfer parameters were introduced. Both the chain scattering parameters and scattering transfer parameters are referred to as $T$ parameters. Be careful to denote which form is being used.

Example $\PageIndex{1}$: Development of Chain Scattering Parameters

Derive the $T$ parameters of the two-port network to the right using a reference impedance $Z_{0}$.

Figure $\PageIndex{2}$

Solution

$\underline{\text{Derivation of }T_{11}}$

Terminate Port $\mathsf{2}$ in a matched load so that $a_{2} = 0$. Then Equation $\eqref{eq:2}$ becomes $a_{1} = T_{11}b_{2}$ and $b_{1} = T_{21}b_{2}$ so

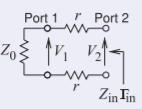
Figure $\PageIndex{3}$

$$\label{eq:9}\Gamma_{\text{in}}=b_{1}/a_{1}=T_{21}/T_{11}$$

Now $Z_{\text{in}}=2r+Z_{0}$, therefore

$$\begin{aligned}\Gamma_{\text{in}}&=\frac{Z_{\text{in}}-Z_{0}}{Z_{\text{in}}+Z_{0}} \\ &=\frac{2r+Z_{0}-Z_{0}}{2r+Z_{0}+Z_{0}}=\frac{r}{r+Z_{0}}\end{aligned}\nonumber$$

Thus

$$\label{eq:10}\Gamma_{\text{in}}=\frac{T_{21}}{T_{11}}=\frac{r}{r+Z_{0}}$$

The next stage is relating $b_{2}$ to $a_{1}$ and since both ports have the same reference impedance $a$ and $b$ can be replaced by traveling voltages

$$\begin{aligned}V_{1}=(V_{1}^{+}+V_{1}^{-})&=V_{1}^{+}(1+\Gamma_{\text{in}}) \\ &=V_{1}^{+}\frac{2r+Z_{0}}{r+Z_{0}}\end{aligned}\nonumber$$

Using voltage division (and since $V_{2}^{+} = a_{2} = 0$)

$$\begin{align}V_{2}=V_{2}^{-}&=\frac{Z_{0}}{2r+Z_{0}}V_{1}\nonumber \\ &=V_{1}^{+}\frac{Z_{0}}{2r+Z_{0}}\frac{2r+Z_{0}}{r+Z_{0}}\nonumber \\ V_{2}^{-}&=V_{1}^{+}\frac{Z_{0}}{r+Z_{0}}\nonumber \\ \label{eq:11}T_{11}&=\frac{V_{1}^{+}}{V_{2}^{-}}=\frac{a_{1}}{b_{2}}=\frac{r+Z_{0}}{Z_{0}}\end{align}$$

$\underline{\text{Derivation of }T_{21}}$

Combining Equations $\eqref{eq:10}$ and $\eqref{eq:11}$

$$\label{eq:12}T_{21}=\Gamma_{\text{in}}T_{11}=\frac{r}{r+Z_{0}}\frac{r+Z_{0}}{Z_{0}}=\frac{r}{Z_{0}}$$

$\underline{\text{Derivation of }T_{22}}$

Terminate Port $\mathsf{2}$ in a matched load so that $a_{1} = 0$. Then Equation $\eqref{eq:2}$ becomes

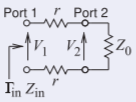
Figure $\PageIndex{4}$

$$\begin{align}0&=T_{11}b_{2}+T_{12}a_{2}\nonumber \\ \label{eq:13}\Gamma_{\text{in}}&=\frac{b_{2}}{a_{2}}=\frac{-T_{12}}{T_{11}}\to T_{12}=-T_{11}\Gamma_{\text{in}} \\ b_{1}&=T_{21}b_{2}+T_{22}a_{2} \\ \label{eq:14}\frac{b_{1}}{a_{2}}&=T_{21}\frac{b_{2}}{a_{2}}+T_{22}\end{align}$$

Now $Z_{\text{in}} = 2r + Z_{0}$ and so

$$\label{eq:15}\Gamma_{\text{in}}=\frac{2r+Z_{0}-Z_{0}}{2r+Z_{0}+Z_{0}}=\frac{r}{r+Z_{0}}$$

Using voltage division

$$\begin{align}V_{1}&=V_{1}^{-}=\frac{Z_{0}}{2r+Z_{0}}V_{2}=\frac{Z_{0}}{2r+Z_{0}}V_{2}^{+}(1+\Gamma_{\text{in}})\nonumber \\ &=V_{2}^{+}\frac{Z_{0}}{2r+Z_{0}}\frac{2r+Z_{0}}{r+Z_{0}}=V_{2}^{+}\frac{Z_{0}}{r+Z_{0}}\nonumber \\ \label{eq:16}\frac{V_{1}^{-}}{V_{2}^{+}}&=\frac{b_{1}}{a_{2}}=\frac{Z_{0}}{r+Z_{0}}\end{align}$$

Substituting Equations $\eqref{eq:15}$ and $\eqref{eq:16}$ in Equation $\eqref{eq:14}$ and rearranging

$$T_{22}=\frac{Z_{0}}{r+Z_{0}}-T_{21}\frac{r}{r+Z_{0}}\nonumber$$

Combining this with Equation $\eqref{eq:12}$

$$\label{eq:17}T_{22}=\frac{Z_{0}}{r+Z_{0}}-\frac{r}{Z_{0}}\frac{r}{r+Z_{0}}=\frac{Z_{0}^{2}-r^{2}}{Z_{0}(r+Z_{0})}$$

$\underline{\text{Derivation of }T_{12}}$

Combining Equations $\eqref{eq:11}$, $\eqref{eq:13}$ and $\eqref{eq:15}$

$$\label{eq:18}T_{12}=-\frac{r+Z_{0}}{Z_{0}}\frac{r}{r+Z_{0}}=-\frac{r}{Z_{0}}$$

$\underline{\text{Summary}}$:

The chain scattering matrix $(T)$ parameters are given in Equations $\eqref{eq:11}$, $\eqref{eq:12}$, $\eqref{eq:17}$, and $\eqref{eq:18}$.

Example $\PageIndex{2}$: Cascading Chain Scattering Parameters

Develop the chain scattering parameters of the network to the right. Use a reference impedance $Z_{\text{REF}} = Z_{0}$, the characteristic impedance of the lines.

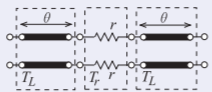
Figure $\PageIndex{5}$

Solution

The network comprises a transmission line of electrical length $\theta$ in cascade with a resistive network and another line of the same electrical length. From Equation (2.5.3) the scattering parameters of the transmission line are

$$\label{eq:19}\mathbf{S}_{L}=\left[\begin{array}{cc}{0}&{\text{e}^{-\jmath\theta}}\\{\text{e}^{-\jmath\theta}}&{0}\end{array}\right]$$

From Equation $\eqref{eq:4}$ the chain scattering matrix of the line is

$$\label{eq:20}\mathbf{T}_{L}=\left[\begin{array}{cc}{\text{e}^{\jmath\theta}}&{0}\\{0}&{\text{e}^{-\jmath\theta}}\end{array}\right]$$

From Example $\PageIndex{1}$ the chain scattering matrix of the resistive network is

$$\label{eq:21}\mathbf{T}_{r}=\frac{1}{Z_{0}}\left[\begin{array}{cc}{gr+Z_{0}}&{-r}\\{r}&{(Z_{0}^{2}-r^{2})/(r+Z_{0})}\end{array}\right]$$

Yielding the chain scattering matrix of the cascade;

$$\label{eq:22}\begin{array}{l}{T_{LrL}=T_{L}T_{r}T_{L}} \\ {\frac{1}{Z_{0}}\left[\begin{array}{cc}{(r+Z_{0})\text{e}^{2\jmath\theta}}&{-r}\\{r}&{(Z_{0}^{2}-r^{2})/(r+Z_{0})\text{e}^{-2\jmath\theta}}\end{array}\right]}\end{array}$$

Example $\PageIndex{3}$: Input Reflection Coefficient of a Terminated Two-Port

What is the input reflection coefficient in terms of chain scattering parameters of the terminated two-port to the right where the two-port is described by its chain scattering parameters.

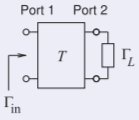
Figure $\PageIndex{6}$

Solution

The chain scattering parameter relations are

$$\left[\begin{array}{c}{a_{1}}\\{b_{1}}\end{array}\right]=\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]\left[\begin{array}{c}{b_{2}}\\{a_{22}}\end{array}\right]\nonumber$$

Expanding this matrix equation and using the substitution $a_{2} = \Gamma_{L}b_{2}$

$$\begin{align}\label{eq:23}a_{1}&=T_{11}b_{2}+T_{12}\Gamma_{L}b_{2} \\ \label{eq:24}b_{1}&+T_{21}b_{2}+T_{22}\Gamma_{L}b_{2}\end{align}$$

Multiplying Equation $\eqref{eq:23}$ by $(T_{21} + T_{22}\Gamma_{L})$ and Equation $\eqref{eq:24}$ by $(T_{11} +T_{12}\Gamma_{L})$ and then subtracting

$$\begin{aligned}(T_{21} + T_{22}\Gamma_{L})a_{1} &= (T_{21} + T_{22}\Gamma_{L})(T_{11}b_{2} + T_{12}\Gamma_{L})b_{2}\nonumber \\ (T_{11} + T_{12}\Gamma_{L})b_{1} &= (T_{11} + T_{12}\Gamma_{L})(T_{21}b_{2} + T_{22}\Gamma_{L})b_{2}\nonumber \\ (T_{21} + T_{22}\Gamma_{L})a_{1} &= (T_{11} + T_{12}\Gamma_{L})b_{1}\nonumber\end{aligned} \nonumber$$

Thus the input reflection coefficient is

$$\label{eq:25}\Gamma_{\text{in}}=\frac{b_{1}}{a_{1}}=\frac{T_{21}+T_{22}\gamma_{L}}{T_{11}+T_{12}\gamma_{L}}$$

Now consider a transmission line of electrical length $\theta$ and characteristic impedance $Z_{0}$ (see the figure b) in cascade with the two-port.

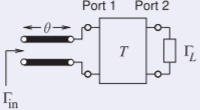
Figure $\PageIndex{7}$

The input reflection coefficient now is found by first determining the total chain scattering matrix of the cascade:

$$\begin{aligned}^{\mathbf{T}}\mathbf{T}&=\mathbf{T}_{\mathbf{L}}\mathbf{T}=\left[\begin{array}{cc}{\text{e}^{\jmath\theta}}&{0}\\{0}&{\text{e}^{-\jmath\theta}}\end{array}\right]\left[\begin{array}{cc}{T_{11}}&{T_{12}}\\{T_{21}}&{T_{22}}\end{array}\right]\nonumber \\ &=\left[\begin{array}{cc}{T_{11}\text{e}^{\jmath\theta}}&{T_{12}\text{e}^{\jmath\theta}}\\{T_{21}\text{e}^{-\jmath\theta}}&{T_{22}\text{e}^{-\jmath\theta}}\end{array}\right]\left[\begin{array}{cc}{^{T}T_{11}}&{^{T}T_{12}}\\{^{T}T_{21}}&{^{T}T_{22}}\end{array}\right]\nonumber\end{aligned} \nonumber$$

Thus the input reflection coefficient is now

$$\begin{align}\Gamma_{\text{in}}&=\frac{b_{1}}{a_{1}}=\frac{^{T}T_{21}+\:^{T}T_{22}\Gamma_{L}}{^{T}T_{11}+\:^{T}T_{12}\Gamma_{L}}\nonumber \\ &=\frac{T_{21}\text{e}^{-\jmath\theta}+T_{22}\text{e}^{-\jmath\theta}\Gamma_{L}}{T_{11}\text{e}^{\jmath\theta}+T_{12}\text{e}^{\jmath\theta}\Gamma_{L}}\nonumber \\ \label{eq:26}&=\text{e}^{-2\jmath\theta}\left(\frac{T_{21}+T_{22}\Gamma_{L}}{T_{11}+T_{12}\Gamma_{L}}\right)\end{align}$$

If the load is now a short circuit $\Gamma_{L} = −1$ and the input reflection coefficient of the line and two-port cascade is

$$\label{eq:27}\Gamma_{\text{in}}=\text{e}^{-2\jmath\theta}\left(\frac{T_{21}-T_{22}}{T_{11}-T_{12}}\right)$$

2.6.1 Terminated Two-Port Network

A two-port with Port 2 terminated in a load with reflection coefficient $\Gamma_{L}$ is shown in Figure 2.7.1 and $a_{2} =\Gamma_{L}b_{2}$. Substituting this in Equation $\eqref{eq:2}$ leads to

$$a_{1} = (T_{11} + T_{12}\Gamma_{L})b_{2}\quad\text{and}\quad b_{1} = (T_{21} + T_{22}\Gamma_{L})b_{2}\nonumber$$

eliminating $b_{2}$ results in

$$\label{eq:28}\Gamma_{\text{in}}=\frac{b_{1}}{a_{1}}=\frac{T_{21}+T_{22}\Gamma_{L}}{T_{11}+T_{12}\Gamma_{L}}$$