2.7: Scattering Parameter Two-Port Relationships
- Page ID
- 41095
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.7.1 Change in Reference Plane
It is often necessary during \(S\) parameter measurements of two-port devices to measure components at a position different from that actually desired. An example is shown in Figure \(\PageIndex{2}\)(a). From direct measurement the \(S\) parameters are obtained, and thus the \(\mathbf{T}\) matrix at Planes \(\mathsf{1}\) and \(\mathsf{2}\). However, \(\mathbf{T}_{\text{DUT}}\) referenced to Planes \(\mathsf{1}'\) and \(\mathsf{2}'\) is required. Now,
\[\label{eq:1}\mathbf{T}=\mathbf{T}_{\theta_{1}}\mathbf{T}_{\text{DUT}}\mathbf{T}_{\theta_{2}} \]
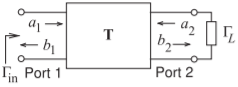
Figure \(\PageIndex{1}\): Terminated two-port network.
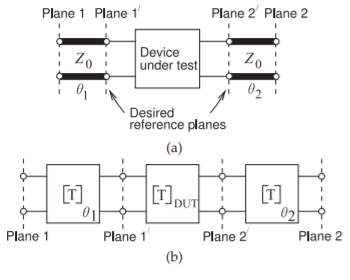
Figure \(\PageIndex{2}\): Two-port measurement setup: (a) a two-port comprising a device under test (\(\text{DUT}\)) and transmission line sections that create a reference plane at Planes \(\mathsf{1}\) and \(\mathsf{2}\); and (b) representation as cascaded two-port networks.
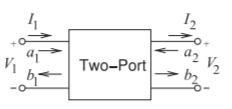
Figure \(\PageIndex{3}\): Two-port with parameters suitable for defining \(S\) and \(ABCD\) parameters.
and so
\[\label{eq:2}\mathbf{T}_{\text{DUT}}=\mathbf{T}_{\theta_{1}}^{-}\mathbf{TT}_{\theta_{2}}^{-1} \]
A section of line with electrical length \(\theta\) and port impedances equal to its characteristic impedance has
\[\label{eq:3}\mathbf{S}=\left[\begin{array}{cc}{0}&{\text{e}^{-\jmath\theta}}\\{\text{e}^{-\jmath\theta}}&{0}\end{array}\right] \]
and
\[\label{eq:4}\mathbf{T}_{\theta}=\left[\begin{array}{cc}{\text{e}^{\jmath\theta}}&{0}\\{0}&{\text{e}^{-\jmath\theta}}\end{array}\right] \]
Therefore Equation \(\eqref{eq:2}\) becomes
\[\label{eq:5}\mathbf{T}_{\text{DUT}}=\left[\begin{array}{cc}{T_{11}\text{e}^{-\jmath(\theta_{1}+\theta_{2})}}&{T_{12}\text{e}^{-\jmath(\theta_{1}-\theta_{2})}} \\ {T_{21}\text{e}^{\jmath(\theta_{1}-\theta_{2})}}&{T_{22}\text{e}^{\jmath(\theta_{1}+\theta_{2})}}\end{array}\right] \]
and then the desired \(S\) parameters of the \(\text{DUT}\) are obtained as
\[\label{eq:6}\mathbf{S}_{\text{DUT}}=\left[\begin{array}{cc}{S_{11}\text{e}^{\jmath 2\theta_{1}}}&{S_{12}\text{e}^{\jmath(\theta_{1}+\theta_{2})}}\\{S_{21}\text{e}^{\jmath(\theta_{1}+\theta_{2})}}&{S_{22}\text{e}^{\jmath 2\theta_{2}}}\end{array}\right] \]
2.7.2 Conversion Between \(S\) and \(ABCD\) Parameters
Figure \(\PageIndex{3}\) can be used to relate the parameters of the two views of the network. If both ports have the same reference impedance \(Z_{0}\), then
\[\left[\begin{array}{c}{V_{1}}\\{I_{1}}\end{array}\right]=\left[\begin{array}{cc}{A}&{B}\\{C}&{D}\end{array}\right]\left[\begin{array}{c}{V_{2}}\\{I_{2}}\end{array}\right]\quad\text{and}\quad\left[\begin{array}{c}{b_{1}}\\{b_{2}}\end{array}\right]=\left[\begin{array}{cc}{S_{11}}&{S_{12}}\\{S_{21}}&{S_{22}}\end{array}\right]\left[\begin{array}{c}{a_{1}}\\{a_{2}}\end{array}\right]\nonumber \]
The \(S\) parameters are then expressed as
\[\label{eq:7}\begin{array}{ll}{S_{11}=\frac{A+B/Z_{0}-CZ_{0}-D}{\Delta}}&{S_{12}=\frac{2(AD-BC)}{\Delta}} \\ {S_{21}=\frac{2}{\Delta}}&{S_{22}=\frac{-A+B/Z_{0}-CZ_{0}+D}{\Delta}}\end{array} \]
where
\[\label{eq:8}\Delta=A+B/Z_{0}+CZ_{0}+D \]
The \(ABCD\) parameters can be expressed in terms of the \(S\) parameters as
\[\begin{align}\label{eq:9}A&=\frac{(1+S_{11})(1-S_{22})+S_{12}S_{21}}{2S_{21}}\\ \label{eq:10}B&=Z_{0}\frac{(1+S_{11})(1+S_{22})-S_{12}S_{21}}{2S_{21}} \\ \label{eq:11}C&=\frac{1}{Z_{0}}\frac{(1-S_{11})(1-S_{22})-S_{12}S_{21}}{2S_{21}} \\ \label{eq:12}D&=\frac{(1-S_{11})(1+S_{22})+S_{12}S_{21}}{2S_{21}}\end{align} \]

