2.1: Introduction
- Page ID
- 41012
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A transmission line stores electric and magnetic energy, and for an alternating signal at a position on the line, energy is converted from one form to the other as time progresses. As such a line has a circuit form that combines inductors, \(L\)s (for the magnetic energy), capacitors, \(C\)s (for the electric energy), and resistors, \(R\)s (modeling losses), whose values depend on the line geometry and material properties.
The transmission lines considered in this chapter are restricted to just two parallel conductors, as shown in Figure \(\PageIndex{1}\), with the distance between the two wires (i.e., in the transverse direction) being substantially smaller than the wavelengths of the signals on the line. The correct physical interpretation is that the conductors of a transmission line confine and guide an EM field. The EM field contains the energy of the signal and not the current on the line.
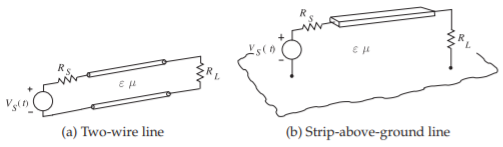
Figure \(\PageIndex{1}\): Two conductor transmission lines.
However, with electrically small transverse dimensions, a two conductor line may be satisfactorily analyzed on the basis of voltages and currents.
The earliest understanding of signal transmission led to telegraphy over distances. The critical theoretical step that enabled transmission over more than short distances was the development of an understanding of signal transmission on lines using phasor analysis [1]. This frequency-domain analysis is still the best way to understand transmission lines. This transmission line theory with modern developments is presented in Section 2.2 and useful formulas and concepts developed in Section 2.3 for lossless transmission lines. Section 2.4 presents several configurations of lossless lines that are particularly useful in microwave circuit design and used in many places in this book series. Section 2.5 repeats the analysis of lossless lines but now for lossy lines. Reflections and transmission of power at multiple interacting interfaces is considered in Section 2.6. Important network models for transmission lines are developed in Section Section 2.7. The last section, Section 2.8, presents summary formulas for many two-conductor transmission lines.
2.1.1 When Must a Line be Considered a Transmission Line
The key determinant of whether a transmission line can be considered as an invisible connection between two points is whether the signal anywhere along the interconnect has the same value at a particular instant. If the value of the signal (say, voltage) varies along the line (at an instant), then it may be necessary to consider transmission line effects. A typical criterion used is that if the length of the interconnect is less than \(1/20\)th of the wavelength of the highest-frequency component of a signal, then transmission line effects can be safely ignored and the circuit can be modeled as a single \(RLC\) circuit [2]. The actual threshold used—\(\lambda/20,\: \lambda/10\), or \(\lambda/5\)—is based on experience and the particular application. For example, an interconnect carrying a digital signal clocking at \(4\text{ GHz}\) has an appreciable frequency component at \(20\text{ GHz}\). Then the interconnect reaches the \(\lambda/10\) threshold when it is \(4.5\text{ mm}\) long. Thus it takes a finite time for the variation of a voltage at one end of the interconnect to impact the voltage at the other end. The ultimate limit is determined by the speed of light, \(c\), but this is reduced by the relative permittivity and permeability of the material in which the fields exist. The relative permittivity and permeability describe the effect of excess potential energy storage in the material, above that of vacuum, in a manner that is analogous to storing mechanical energy in a spring.
2.1.2 Movement of a Signal on a Transmission Line
A coaxial line (Figure \(\PageIndex{2}\)(a)) is the quintessential transmission line as it is one of the few transmission line structures that can be described exactly from first principles when there is no loss. This is because the cross section of a coaxial line matches the cylindrical coordinate system, an orthogonal coordinate system with boundary conditions that can be expressed in terms of just one coordinate (the radius). It is known how to solve Maxwell’s equations,which are just differential equations, in an orthogonal coordinate system. This is done for a coaxial line in Section 2.9.
When a positive voltage pulse is applied to the center conductor of the

Figure \(\PageIndex{2}\): A coaxial transmission line: (a) three-dimensional view; (b) the line with pulsed voltage source showing the electric fields at an instant in time as a voltage pulse travels down the line. \(E_{L} ≪ E_{T}\).

Figure \(\PageIndex{3}\): Fields, currents, and charges on the coaxial transmission line of Figure \(\PageIndex{2}\) at times \(t_{4} > t_{3} > t_{2} > t_{1}\). \(Q_{\text{CENTER}}\) is the net free charge on the center conductor. \(I_{\text{CENTER}}\) is the current on the center conductor.
coaxial line, as shown in Figure \(\PageIndex{2}\)(a), an electric field results that is directed from the center conductor to the outer conductor. Referring to Figure \(\PageIndex{2}\)(b), the component of the field that is directed along the shortest path from the center conductor to the outer conductor is denoted \(E_{T}\), and the subscript \(T\) denotes the transverse component of the field with the transverse plane being perpendicular to the direction of propagation along the line. Figure \(\PageIndex{2}\)(b) shows the fields in the structure after the pulse has started moving along the line. This is shown in another view in Figure \(\PageIndex{3}\) at four different times. The transverse voltage, \(V_{T}\), is given by \(E_{T}\) integrated along a path between the inner and outer conductors: \(V_{T} ≈ E_{T}(a − b)\). This is a good measure, provided that the transverse dimensions are small compared to a wavelength (otherwise the integral is then path dependent). The voltage pulse exciting the line has a trapezoidal shape and Figure \(\PageIndex{3}\) shows the charge, \(Q_{\text{CENTER}}\), and current, \(I_{\text{CENTER}}\), on the center conductor and the transverse field, \(E_{T}\). The voltage between the inner and outer conductor has the same form as \(E_{T}\). As indicated by Maxwell’s equations, a change in time of the electric field results in a spatial change in the magnetic field and hence current. As a result there is a variation of the current in time and this results in a spatial change of the electric field. The chasing from a time variation to a spatial variation and then back to a time variation causes the pulse to move down the line.
The pulse moves down the line at the group velocity, which for a lossless coaxial line is the same as the phase velocity, \(v_{p}\).\(^{1}\) This is determined by the physical properties of the region between the conductors. The permittivity, \(\varepsilon\), describes energy storage associated with the electric field, \(E\), and the energy storage associated with the magnetic field, \(H\), is described by the permeability, \(\mu\). (Both \(\varepsilon\) and \(\mu\) are properties of the medium—the material.) It has been determined that\(^{2}\)
\[\label{eq:1}v_{p}=1/\sqrt{\mu\varepsilon} \]
In a vacuum \(\varepsilon =\varepsilon_{0}\), the free-space permittivity, and \(\mu =\mu_{0}\), the free-space permeability. These are physical constants and have the values
\[\begin{array}{ll}{\text{Permittivity of free space:}}&{\varepsilon_{0}=8.854\times 10^{-12}\text{ F/m}}\\{\text{Permeability of free space:}}&{\mu_{0}=4\pi\times 10^{-7}\text{ H/m}}\end{array}\nonumber \]
One conclusion here is that EM energy can be stored in free space, i.e. in a vacuum. In free space \(v_{p} = c = 1/\sqrt{\mu_{0}\varepsilon_{0}} = 3\times 10^{8}\text{ m/s}\). The free-space wavelengths, \(\lambda_{0} = c/f\), at several frequencies, \(f\), are
| \(f\) | \(100\text{ MHz}\) | \(1\text{ GHz}\) | \(10\text{ GHz}\) |
|---|---|---|---|
| \(\lambda_{0}\) | \(3\text{ m}\) | \(30\text{ cm}\) | \(3.0\text{ cm}\) |
Table \(\PageIndex{1}\)
Commonly \(\lambda_{0}\) is used to indicate the wavelength in free space and \(\lambda_{g}\), the guide wavelength, is used to denote the wavelength on a transmission line. It is convenient to use the relative permittivity (or the less commonly used term dielectric constant), \(\varepsilon_{r}\), defined as
\[\label{eq:2}\varepsilon_{r}=\varepsilon/\varepsilon_{0} \]
Similarly the relative permeability is
\[\label{eq:3}\mu_{r}=\mu/\mu_{0} \]
and most materials have \(\mu_{r} = 1\). The permittivity, permeability, and conductivity of materials used in RF and microwave circuits are given in Appendix 2.A.
A length of coaxial line is filled with a dielectric having a relative permittivity of \(20\) and is designed to be \(1/4\) wavelength long at a frequency, \(f\), of \(1.850\text{ GHz}\).
- What is the free-space wavelength?
- What is the wavelength of the signal in the dielectric-filled coaxial line?
- How long is the line?
Solution
- \(\lambda_{0} = c/f = 3\times 10^{8}/1.85\times 10^{9} = 0.162\text{ m} = 16.2\text{ cm}\).
- Note that for a dielectric-filled line with \(\mu_{r} = 1,\:\lambda = v_{p}/f = c/(\sqrt{\varepsilon_{r}}f) = \lambda_{0}/\sqrt{\varepsilon_{r}}\), so \(\lambda =\lambda_{0}/\sqrt{\varepsilon_{r}} = 16.2\text{ cm}/ \sqrt{20} = 3.62\text{ cm}\).
- \(\lambda_{g}/4=3.62\text{ cm}/4=9.05\text{ mm}\).
Footnotes
[1] The phase velocity is the apparent velocity of a point of constant phase on a sinewave and is almost frequency independent for a low-loss coaxial line of small transverse dimensions (less than \(\lambda/10\)).
[2] This is derived from Maxwell’s equations and describes the situation where the fields have a very simple structure, in general where the fields are solely directed in the transverse plane.


