2.2: Transmission Line Theory
- Page ID
- 41013
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This section develops the theory of signal propagation on transmission lines. The first section, Section 2.2.1, makes the argument that a circuit with resistors, inductors, and capacitors is a good model for a transmission line. The complete development of transmission line theory is presented in Section 2.2.2, and Section 2.2.3 relates the RLGC transmission line model to the properties of a medium. The dimensions of some of the quantities that appear in transmission line theory are discussed in Section 2.2.4. Section 2.2.5 summarizes the important parameters of a lossless line and then two particularly important lines, coaxial lines and microstrip lines, are considered in Sections 2.2.6 and 2.2.7.
2.2.1 Transmission Line RLGC Model
Regardless of the actual structure, a segment of uniform transmission line (i.e., a line with constant cross section along its length) as shown in Figure \(\PageIndex{1}\)(a) can be modeled by the circuit shown in Figure \(\PageIndex{1}\)(b) with
\[\left.\begin{array}{lr}{\text{Resistance along the line}}&{=R} \\ {\text{Inductance along the line}}&{=L} \\ {\text{Conductance shunting the line}}&{=G} \\ {\text{Capacitance shunting the line}}&{=C}\end{array}\right| \begin{array}{l}{}\\{\text{all specified}} \\ {\text{per unit length}}\\{}\end{array}\nonumber \]
Thus \(R,\: L,\: G\), and \(C\) are also referred to as resistance, inductance, conductance, and capacitance per unit length. (Sometimes p.u.l. is used as shorthand for per unit length.) In the metric system, ohms per meter (\(Ω\text{/m}\)), henries per meter (\(\text{H/m}\)), siemens per meter (\(\text{S/m}\)) and farads per meter (\(\text{F/m}\)), respectively, are used. The values of \(R,\: L,\: G\), and \(C\) are affected by the geometry of the transmission line and by the electrical properties of the dielectrics and conductors. \(C\) describes the ability to store electrical energy and is mostly due to the properties of the dielectric. \(G\) describes loss in the dielectric which derives from conduction in the dielectric and from dielectric relaxation. Most microwave substrates have negligible conductivity so dielectric relaxation loss dominates. Dielectric relaxation loss results from the movement of charge centers which result in distortion of the dielectric lattice (if a crystal) or molecular structure. The periodic variation of the \(E\) field transfers energy from the EM field to mechanical vibrations. \(R\) is due to ohmic loss in the metal more than anything else. \(L\) describes the ability to store magnetic energy and is mostly a function of geometry, as most materials used with transmission lines have \(\mu_{r} = 1\) (so no more magnetic energy is stored than in a vacuum).
For most lines the effects due to \(L\) and \(C\) dominate because of the relatively low series resistance and shunt conductance. The propagation characteristics of the line are described by its loss-free, or lossless, equivalent line, although in practice some information about \(R\) or \(G\) is necessary to determine power
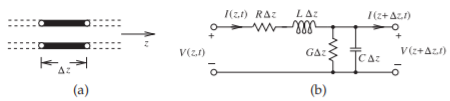
Figure \(\PageIndex{1}\): Transmission line segment: (a) of length \(\Delta z\); and (b) lumped-element model.
losses. The lossless concept is just a useful and good approximation.
2.2.2 Derivation of Transmission Line Properties
In this section the differential equations governing the propagation of signals on a transmission line are derived. These are coupled first-order differential equations and are akin to Maxwell’s Equations in one dimension. Solution of the differential equations describes how signals propagate, and leads to the extraction of a few parameters that describe transmission line properties.
Applying Kirchoff’s laws applied to the model in Figure \(\PageIndex{1}\)(b) and taking the limit as \(\Delta z\to 0\) the transmission line equations are
\[\begin{align}\label{eq:1}\frac{\partial v(z,t)}{\partial z}&=-Ri(z,t)-L\frac{\partial i(z,t)}{\partial t} \\ \label{eq:2}\frac{\partial i(z,t)}{\partial z}&=-Gv(z,t)-C\frac{\partial v(z,t)}{\partial t}\end{align} \]
\(V(z)\) is a phasor and \(v(z, t) = \Re\{ V(z)e^{\jmath\omega t}\}\). \(\Re\{w\}\) denotes the real part of \(w\), a complex number.
In sinusoidal steady-state using cosine-based phasors these become
\[\label{eq:3}\frac{dV(z)}{dz}=-(R+\jmath\omega L)I(z) \]
and
\[\label{eq:4}\frac{dI(z)}{dz}=-(G+\jmath\omega C)V(z) \]
Eliminating \(I(z)\) in the above yields the wave equation for \(V(z)\):
\[\label{eq:5}\frac{d^{2}V(z)}{dz^{2}}-\gamma^{2}V(z)=0 \]
Similarly
\[\label{eq:6}\frac{d^{2}I(z)}{dz^{2}}-\gamma^{2}I(z)=0 \]
where the propagation constant is
\[\label{eq:7}\gamma =\alpha +\jmath\beta =\sqrt{(R+\jmath\omega L)(G+\jmath\omega C)} \]
with SI units of \(\text{m}^{−1}\) and where \(\alpha\) is the attenuation coefficient and has units of nepers per meter (\(\text{Np/m}\)), and \(\beta\) is the phase-change coefficient, or phase constant, and has units of radians per meter (expressed as \(\text{rad/m}\) or radians/m). Nepers and radians are dimensionless units, but serve as prompts for what is being referred to.
Equations \(\eqref{eq:5}\) and \(\eqref{eq:6}\) are second-order differential equations that have solutions of the form
\[\label{eq:8}V(z)=V_{0}^{+}e^{-\gamma z}+V_{0}^{-}e^{\gamma z} \]
and
\[\label{eq:9}I(z)=I_{0}^{+}e^{-\gamma z}+I_{0}^{-}e^{\gamma z} \]
The physical interpretation of these solutions is that \(V^{+}(z) = V_{0}^{+}e^{−\gamma z}\) and \(I^{+}(z) = I_{0}^{+}e^{−\gamma z}\) are forward-traveling waves (moving in the \(+z\) direction) and \(V^{−}(z) = V_{0}^{−}e^{\gamma z}\) and \(I^{−}(z) = I_{0}^{−}e^{\gamma z}\) are backward-traveling waves (moving in the \(−z\) direction). \(V(z),\: V_{0}^{+},\: V_{0}^{−},\: I(z),\: I_{0}^{+}\) and \(I_{0}^{−}\) are all phasors. Substituting Equation \(\eqref{eq:8}\) in Equation \(\eqref{eq:3}\) results in
\[\label{eq:10}I(z)=\frac{\gamma}{R+\jmath\omega L}\left[ V_{0}^{+}e^{-\gamma z}-V_{0}^{-}e^{\gamma z}\right] \]
Then from Equations \(\eqref{eq:10}\) and \(\eqref{eq:9}\)
\[\label{eq:11}I_{0}^{+}=\frac{\gamma}{R+\jmath\omega L}V_{0}^{+}\quad\text{and}\quad I_{0}^{-}=\frac{\gamma}{R+\jmath\omega L}(-V_{0}^{-}) \]
The characteristic impedance is defined as
\[\label{eq:12}Z_{0}=\frac{V_{0}^{+}}{I_{0}^{+}}=\frac{-V_{0}^{-}}{I_{0}^{-}}=\frac{R+\jmath\omega L}{\gamma}=\sqrt{\frac{R+\jmath\omega L}{G+\jmath\omega C}} \]
with the SI unit of ohms (\(\Omega\)). Equations \(\eqref{eq:8}\) and \(\eqref{eq:9}\) can be rewritten as
\[\label{eq:13}V(z)=V_{0}^{+}e^{-\gamma z}+V_{0}^{-}e^{\gamma z} \]
and
\[\label{eq:14}I(z)=\frac{V_{0}^{+}}{Z_{0}}e^{-\gamma z}-\frac{V_{0}^{-}}{Z_{0}}e^{\gamma z} \]
Converting back to the time domain:
\[\label{eq:15} v(z,t)=|V_{0}^{+}|\cos(\omega t-\beta z+\varphi^{+})e^{-\alpha z}+|V_{0}^{-}|\cos(\omega t+\beta z+\varphi^{-})e^{\alpha z} \]
where \(\varphi^{+}\) and \(\varphi^{-}\) are phases of the forward- and backward-traveling waves, respectively. The phasors of the traveling voltage waves are
\[\label{eq:16}V_{0}^{+}(z)=|V_{0}^{+}|e^{\jmath\varphi^{+}}e^{-\jmath\beta z}\quad\text{and}\quad V_{0}^{-}(z)=|V_{0}^{-}|e^{\jmath\varphi^{-}}e^{\jmath\beta z} \]
The following quantities are defined:
\[\begin{align}\label{eq:17} \text{Characteristic impedance:} \quad&Z_{0}=\sqrt{(R+\jmath\omega L)/(G+\jmath\omega C)} \\ \label{eq:18}\text{Propagation constant:} \quad&\gamma =\sqrt{(R+\jmath\omega L)(G+\jmath\omega C)} \\ \label{eq:19} \text{Attenuation constant:} \quad&\alpha =\Re\{\gamma\} \\ \label{eq:20}\text{Phase constant:} \quad&\beta=\Im\{\gamma\} \\ \label{eq:21}\text{Wavenumber:} \quad& k=-\jmath\gamma \\ \label{eq:22}\text{Phase velocity:}\quad&v_{p}=\omega/\beta \\ \label{eq:23}\text{Wavelenght:}\quad&\lambda=\frac{2\pi}{|\gamma|}=\frac{2\pi}{|k|}\end{align} \]
where \(\omega = 2\pi f\) is the radian frequency and \(f\) is the frequency with the SI units of hertz (\(\text{Hz}\)). The wavenumber \(k\) as defined here is used in electromagnetics and where wave propagation is concerned. Considering one of the traveling waves, the phase velocity refers to the apparent velocity of which a point of constant phase on the sinewave appears to move.
For low-loss materials, \(\alpha ≪\beta\), and so \(\beta ≈ |k|\), then the following approximations are valid:
\[\begin{align}\label{eq:24}\text{Characteristic impedance:}\quad&Z_{0}\approx\sqrt{L/C} \\ \label{eq:25}\text{Phase constant:}\quad&\beta\approx\omega\sqrt{LC} \\ \label{eq:26}\text{Wavenumber:}\quad&k\approx\beta \\ \label{eq:27}\text{Phase velocity:}\quad&v_{p}=\omega/\beta \\ \label{eq:28}\text{Wavelength:}\quad&\lambda\approx\frac{2\pi}{\beta}=v_{p}/f\end{align} \]
The important result here is that a voltage wave (and a current wave) can be defined on a transmission line. One more parameter needs to be introduced: the group velocity,
\[\label{eq:29}v_{g}=\frac{\partial\omega}{\partial\beta} \]
The group velocity is the velocity of a modulated waveform’s envelope and describes how fast information propagates. It is the velocity at which the energy (i.e. information) in the waveform moves. Thus group velocity can never be more than the speed of light in a vacuum, \(c\). Phase velocity, however, can be more than \(c\). If the speed at which information moves varies with frequency, then a signal such as a pulse will spread out. Such a line is said to have dispersion. For a lossless, dispersionless line, the group and phase velocity are the same. If the phase velocity is frequency independent, then \(\beta\) is linearly proportional to \(\omega\).
Electrical length is used in designs with transmission lines prior to establishing the physical length of the line. The electrical length of a line is expressed either as a fraction of a wavelength or in degrees (or radians), where a wavelength corresponds to \(360^{\circ}\) (or \(2π\) radians). So if \(\beta\) is the phase constant of a signal on the line and \(ell\) is its physical length, the electrical length of the line in radians is \(\beta\ell\).
A transmission line is \(10\text{ cm}\) long and at the operating frequency the phase constant \(\beta\) is \(30\text{ rad/m}\). What is the electrical length of the line?
Solution
The physical length of the line is \(\ell = 10\text{ cm} = 0.1\text{ m}\). Then the electrical length of the line is \(\ell_{e} = \beta\ell = (30\text{ rad/m})\times 0.1\text{ m} = 3\text{ radians}\). The electrical length can also be expressed in terms of wavelength noting that \(360^{\circ}\) corresponds to \(2π\) radians, which also corresponds to \(\lambda\). Thus \(\ell_{e} = (3\text{ radians})=3\times 360/(2π) = 171.9^{\circ}\) or \(\ell_{e} = 3/(2π)\lambda = 0.477\lambda\).
A transmission line has the \(RLGC\) parameters \(R = 100\: Ω\text{/m},\: L = 80\text{ nH/m},\: G = 1.6\text{ S/m}\), and \(C = 200\text{ pF/m}\). Consider a traveling wave at \(2\text{ GHz}\) on the line.
- What is the attenuation constant?
- What is the phase constant?
- What is the phase velocity?
- What is the characteristic impedance of the line?
- What is the group velocity?
Solution
- \(\alpha:\:\gamma =\alpha +\jmath\beta = \sqrt{(R + \jmath\omega L) (G +\jmath\omega C)};\:\quad\omega = 12.57\cdot 10^{9}\text{ rad/s}\)
\[\begin{aligned}\gamma&=\sqrt{(100 +\jmath\omega\cdot 80\cdot 10^{−9}) (1.6 +\jmath\omega 200\times 10^{−12})}=(17.94 + \jmath 51.85)\text{ m}^{−1} \\ \alpha&=\Re\{\gamma\}=17.94\text{ Np/m}\nonumber\end{aligned} \nonumber \] - Phase constant:
\[\beta = \Im\{\gamma\} = 51.85\text{ rad/m}\nonumber \] - Phase velocity"
\[v_{p}=\frac{\omega}{\beta}=\frac{2\pi f}{\beta}=\frac{12.57\times 10^{9}\text{ rad}\cdot\text{s}^{-1}}{51.85\text{ rad}\cdot\text{m}^{-1}}=2.42\times 10^{8}\text{ m/s}\nonumber \] - \(Z_{0} = (R +\jmath\omega L)/\gamma = (100 + \jmath\omega\cdot 80\cdot 10^{−9})/(17.94 + \jmath 51.85) = (17.9 + \jmath 4.3)\:\Omega\)
Note also that \(Z_{0} = \sqrt{(R + \jmath\omega L)/(G + \jmath\omega C)}\), which yields the same answer. - Group velocity:
\[v_{g}=\left.\frac{\partial\omega}{\partial\beta}\right|_{f=2\text{ GHz}}\nonumber \]
Numerical derivatives will be used, thus \(v_{g} = \Delta\omega/\Delta\beta\). Now \(\beta\) is already known at \(2\text{ GHz}\). At \(1.9\text{ GHz}\), \(\gamma = 17.884 + \jmath 49.397\text{ m}^{−1}\), and so \(\beta = 49.397\text{ rad/m}\).
\[v_{g}=\frac{2π(2\text{ GHz} − 1.9\text{ GHz})}{\beta(2\text{ GHz}) − \beta(1.9\text{ GHz})}=\frac{2π(2 − 1.9)10^{9}\text{ Hz}}{(51.85 − 49.397)\text{ m}^{−1}}=2.563\times 10^{8}\text{ m/s}\nonumber \]
(Note that \(\text{Hz} = \text{s}^{−1}\). Note that \(v_{g}\neq v_{p}\), and so the transmission line has dispersion.)
2.2.3 Relationship of RLGC parameters to Permittivity and Permeability of a Medium
In the previous section the telegrapher’s equations for a transmission line modeled as subsections of \(RLGC\) elements was derived. Very good accuracy is obtained if the length of a subsection is no more than one-twentieth of a wavelength. The full transmission line model is the cascade of many transmission line subsections (e.g. see Figure \(\PageIndex{2}\)). In this section the \(RLGC\) parameters are related to the physical parameters of permittivity and permeability. The development does not go into much detail, as the derivation is involved and can only be derived analytically for a few regular transmission line structures. If you are curious, the development is done for a parallel plate waveguide and a rectangular waveguide in Chapter 6 and for a coaxial line in Section 2.9.
The main parameters describing propagation on a transmission line are \(Z_{0}\) and \(\gamma\), and these depend on the permeability and permittivity of the medium and the spatial variation of the \(E\) and \(H\) fields resulting from the geometry of the conductors. Only a few geometries permit analytic solution of the fields so in general a numerical field solution is required and \(Z_{0}\) and \(\gamma\) derived. Very often equations are curve fit to the numerical solutions but the structure of the equations have a theoretical foundation. It is found that there can be a number of possible field solutions (not unusual for the solution of differential equations) each of which is called a mode. Modes that have all the fields in the transverse plane (perpendicular to the propagation direction) is called a transverse EM (TEM) mode and these modes exist at DC. The other modes are only possible above a cut-off frequency. It is found that the propagation constant has the form
\[\label{eq:30}\gamma^{2}=-(k^{2}-k_{c}^{2}) \]
where \(k_{c}\) is the cutoff wavenumber and for a particular line usually has a different value for each mode. The wavenumber of a homogeneous line is
\[\label{eq:31}k=\jmath\omega\sqrt{\mu\varepsilon} \]
A mode can only exist and describe a propagating signal when \(\beta = \Im\{\gamma\}\) is not zero which requires that \(\gamma^{2}\) be negative. Thus a mode can support a propagating mode only if the wavenumber is greater than the cut-off wavenumber, i.e. when \(k>k_{c}\). A TEM mode has \(k_{c} = 0\) so a signal, other than DC can always propagate on the line in a TEM mode. A homogeneous line has just one type of medium supporting the EM fields. An example of a homogeneous line is a teflon-filled coaxial line. A non-homogeneous line has two or or more dielectric mediums, such as air and a dielectric. For nonhomogeneous lines the concept of an equivalent homogeneous line with an effective permittivity \(\varepsilon_{\text{eff}}\) and effective permeability \(\mu_{\text{eff}}\) is used. Then
\[\label{eq:32}k=\jmath\omega\sqrt{\mu_{\text{eff}}\varepsilon_{\text{eff}}} \]

Figure \(\PageIndex{2}\): \(RLGC\) model of a transmission line.
Loss is incorporated in the imaginary parts of \(\varepsilon\) and \(\mu\) for TEM modes. As before, for any mode,
\[\begin{align}\label{eq:33}\text{Attenuation constant:}\quad&\alpha=\Re\{\gamma\} \\ \label{eq:34}\text{Phase constant:}\quad&\beta=\Im\{\gamma\} \\ \label{eq:35}\text{Phase velocity:}\quad&v_{p}=\omega/\beta \\ \label{eq:36}\text{Wavelength:}\quad&\lambda=\frac{v_{p}}{f}=\frac{2\pi}{\beta}\end{align} \]
Comparing \(\gamma\) in Equations \(\eqref{eq:7}\) and \(\eqref{eq:32}\), an equivalence can be developed between the lumped-element form of transmission line propagation and the propagation of an EM wave in a medium. Specifically,
\[\label{eq:37}-\omega^{2}\mu_{\text{eff}}\varepsilon_{\text{eff}}=(R+\jmath\omega L)(G+\jmath\omega C) \]
Lossless Medium
If the medium is lossless (\(\mu\) and \(\varepsilon\) are real and \(R =0= G\)), then
\[\label{eq:38}\mu_{\text{eff}}\varepsilon_{\text{eff}}=LC \]
When the medium is free space (a vacuum), then a subscript zero is used. Free space is also lossless, so the following results hold:
\[\label{eq:39}\alpha_{0}=0\quad\text{and}\quad\beta_{0}=-\jmath\gamma=\omega\sqrt{\mu_{0}\varepsilon_{0}}=\omega\sqrt{LC} \]
If frequency is specified in gigahertz (indicated by \(f_{\text{GHz}}\)), in free space
\[\label{eq:40}\beta_{0}=20.958\:f_{\text{GHz}}\quad\text{units of rads/m} \]
At \(1\text{ GHz}\), \(\beta_{0} = 20.958\text{ rad/m}\) and \(\lambda_{0} = 29.98\text{ cm}\) (use \(\lambda_{0}\approx 30\text{ cm}\) at \(1\text{ GHz}\) as a reference). In a lossless medium with effective relative permeability \(\mu_{e} = \mu_{\text{eff}}/\mu_{0} = 1\) and effective relative permittivity \(\varepsilon_{e} = \varepsilon_{\text{eff}}/\varepsilon_{0}\),
\[\label{eq:41}\beta=\sqrt{\varepsilon_{e}}\beta_{0} \]
\(Z_{0}\) depends strongly on the spatial variation of the fields. When there is no variation in the plane transverse to the direction of propagation (i.e. for plane wave propagation)
\[\label{eq:42}Z_{0}=\sqrt{\mu/\varepsilon} \]
However, if there is variation of the fields
\[\label{eq:43}Z_{0}=\kappa\sqrt{\mu_{\text{eff}}/\varepsilon_{\text{eff}}}=\kappa\sqrt{\mu_{0}/\varepsilon_{0}}\sqrt{\mu_{e}/\varepsilon_{e}} \]
where \(\kappa\) captures the effect of geometric variation of the fields. Spatial variation of the fields stores additional energy in the \(E\) and \(H\) fields, affecting \(\gamma\) as well as \(Z_{0}\).
If the boundary conditions on a transmission line are such that a required spatial variation of the fields cannot be supported, then the signal cannot propagate. The critical frequency at which \(k =\jmath\omega\sqrt{\mu\varepsilon} = k_{c}\) is called the cutoff frequency, \(f_{c}\). Signals cannot propagate on the line if the frequency is below \(f_{c}\). For the rest of this chapter the only lines considered are those for which \(k_{c} = 0\), (and \(f_{c} = 0\)), i.e. TEM modes on transmission lines. That is, the lines carry DC signals.
Low Loss Medium
Transmission line loss is due to the resistance of conductors, which is described by \(R\), and loss in the dielectric described by \(G\). For most dielectrics there is very little conductive loss and loss is due almost entirely to dielectric relaxation. (The most common exception is when the dielectric is silicon as there can be appreciable conduction in silicon.) In dielectric relaxation an electric field causes charge centers to move and these cause the lattice to vibrate which we know is heat so energy is transferred from the electric field to heat. The energy lost is proportional to frequency and so \(G\) is directly proportional to frequency and consequently, provided there is no conduction in the dielectric, the loss tangent of the transmission line is thus defined as:
\[\label{eq:44}\tan\delta =G\omega C=\text{ independent of frequency} \]
One consequence of Equation \(\eqref{eq:44}\), and noting that \(C\) is approximately independent of frequency, is that if \(G\) is known at one frequency then its value at another frequency can be quickly determined.
The loss tangent of the dielectric medium and the loss tangent of the transmission line may not be the same as the EM fields may not be confined just to the medium, e.g. fields are in air and in a dielectric.
2.2.4 Dimensions of \(\gamma,\:\alpha,\) and \(\beta\)
The SI unit of \(\gamma\) are inverse meters (\(\text{m}^{−1}\)) and the attenuation constant, \(\alpha\), and the phase constant, \(\beta\), have, strictly speaking, the same units. However, the convention is to introduce the dimensionless quantities Neper and radian to convey additional information. Thus the attenuation constant \(\alpha\) has the units of Nepers per meter (\(\text{Np/m}\)) and the phase constant \(\beta\) has the units radians per meter (\(\text{rad/m}\)). The unit Neper comes from the name of the \(\text{e} (= 2.7182818284590452354...)\) symbol (written in upright font and not italics since it is a constant), which is called the Neper. The Neper is used in calculating transmission line signal levels, as in Equations \(\eqref{eq:8}\) and \(\eqref{eq:9}\). The attenuation and phase constants are often separated and then the attenuation constant describes the decrease in signal amplitude as the signal travels down a transmission line. So when \(\alpha\ell = 1\text{ Np}\), where \(\ell\) is the length of the line, the signal has decreased to \(1/\text{e}\) of its original value, and the power drops to \(1/\text{e}^{2}\) of its original value. The decrease in signal level represents loss and the units of decibels per meter (\(\text{dB/m}\)) are used with \(1\text{ Np} = 20 \log \text{e} = 8.6858896381\text{ dB}\). So expressing \(\alpha\) as \(1\text{ Np/m}\) is the same as saying that the attenuation loss is \(8.6859\text{ dB/m}\). To convert from \(\text{dB}\) to \(\text{Np}\) multiply by \(0.1151\). Thus \(\alpha = x\text{ dB/m} = x\times 0.1151\text{ Np/m}\).
The name for e derives from John Napier, who developed the theory of logarithms [3]. \(\text{e}\) is sometimes called Euler’s constant.
In engineering \(\log x ≡ \log_{10} x\) and \(\ln x ≡ \log_{e} x\).
A line has an attenuation of \(10\text{ dB/m}\) and a phase constant of \(50\text{ radians/m}\) at \(2\text{ GHz}\).
- What is the complex propagation constant of the transmission line?
- If the capacitance of the line is \(100\text{ pF/m}\) and the conductive loss is zero (i.e., \(G = 0\)), what is the characteristic impedance of the line?
Solution
- \(\alpha|_{\text{Np}} = 0.1151\times \alpha|_{\text{dB}} = 0.1151\times (10\text{ dB/m}) = 1.151\text{ Np/m},\:\beta = 50\text{ rad/m}\)
Propagation constant, \(\gamma =\alpha +\jmath\beta = (1.151 + \jmath 50)\text{ m}^{−1}\) - \(\gamma =\sqrt{(R +\jmath\omega L) (G +\jmath\omega C)}\), and \(Z_{0} = \sqrt{(R +\jmath\omega L)/(G +\jmath\omega C)}\),
therefore \(Z_{0} = \gamma /(G + \jmath\omega C)\); \(\omega = 2π\cdot 2\times 10^{9}\text{ s}^{−1}\); \(G = 0\); \(C = 100 \times 10^{−12}\text{ F}\), so \(Z_{0} = 39.8 −\jmath 0.916\:\Omega\).
2.2.5 Lossless Transmission Line
If the conductor and dielectric are ideal (i.e., lossless), then \(R =0= G\) and the equations for the transmission line characteristics simplify. The transmission line parameters from Equations \(\eqref{eq:12}\) and \(\eqref{eq:18}\)–\(\eqref{eq:23}\) are then
\[\begin{align}\label{eq:45}Z_{0}&=\sqrt{\frac{L}{C}} \\ \label{eq:46}\beta&=\omega\sqrt{LC} \\ \label{eq:47}\lambda_{g}&=\frac{2\pi}{\omega\sqrt{LC}}=\frac{v_{p}}{f} \\ \label{eq:48}\alpha&=0 \\ \label{eq:49}v_{p}&=1/\sqrt{LC}\end{align} \]
Note that there is a distinction between a transmission line and an RLC circuit. When a transmission line is referred to as having an impedance of \(50\:\Omega\), this is referring to the line having a characteristic impedance of \(50\:\Omega\), the line cannot be replaced by a \(50\:\Omega\) resistor.
A line cannot be replaced by a lumped element except as follows:
- When calculating the forward voltage wave of a line that is infinitely long (or there are no reflections from the load). Then the line can be replaced by an impedance equal to the characteristic impedance of the line. The total voltage is then only the forward-traveling component.
- The characteristic impedance and load impedance are used to calculate the input impedance of the terminated line at a particular frequency.
2.2.6 Coaxial Line
The analytic calculation of the characteristic impedance of a transmission line from geometry is not always possible except for a few regular geometries (matching orthogonal coordinate systems). For a coaxial line, the electric fields extend in a radial direction from the center conductor to the outer conductor. So it is possible to calculate the voltage by integrating this \(E\) field from the center to the outer conductor. The magnetic field is circular, centered on the center conductor, so the current on the conductor can be calculated as the closed integral of the magnetic field. (Here the field lines and the conductor boundaries correspond to the cylindrical coordinate system.) Solving for the fields in the region between the center and outer conductors yields the following formula for the characteristic impedance of a coaxial line (the derivation is presented in Section 2.9):
\[\label{eq:50}Z_{0}=138\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\log\left(\frac{b}{a}\right)\:\Omega =60\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left(\frac{b}{a}\right)\:\Omega \]
where \(\varepsilon_{r}\) is the relative permittivity of the medium between the center and outer conductors, \(b\) is the inner diameter of the outer conductor, and \(a\) is the outer diameter of the inner conductor. With a higher \(\varepsilon\), more energy is stored in the electric field and the capacitance per unit length of the line, \(C\), increases. As the relative permittivity of the line increases, the characteristic impedance of the line reduces. Equation \(\eqref{eq:50}\) is an exact formulation for the characteristic impedance of a coaxial line. Such a formula can only be approximated for nearly every other line.
Most coaxial cables have \(Z_{0}\) of \(50\:\Omega\), but different ratios of b and a yield special properties of the coaxial line. When the ratio is \(1.65\) for an air-filled line, \(Z_{0} = 30\:\Omega\) and the line has maximum power-carrying capability. The

Figure \(\PageIndex{3}\): Coaxial line adaptors: (a) N-type female-to-female (N(f)-to-N(f)); (b) APC-7 to Ntype male (APC-7-to-N(m)); (c) APC-7 to SMA-type male (APC-7-to-SMA(m)); SMA adapters: (d) SMA-type female-to-female (SMA(f)-to-SMA(f)); (e) SMA-type male-to-female (SMA(m)-toSMA(f)); (f) SMA-type male-to-male (SMA(m)-to-SMA(m)); and (g) SMA elbow. N, APC-7 and SMA are known as connector series.
ratio for maximum voltage breakdown is \(2.7\), corresponding to \(Z_{0} = 60\:\Omega\) for an air-filled line. The characteristic impedance for minimum attenuation in an air-filled line is \(77\:\Omega\), with a diameter ratio of \(3.59\). This optimum ratio of outer-to-inner conductors for minimum loss is independent of the dielectric and typical dielectrics have negligible loss with line loss due almost entirely due to the conductors. If the dielectric filling the coaxial line is polyethylene (which is most common) with \(\varepsilon_{r} = 2.3\), the characteristic impedance of the minimum loss line is \(50.6\:\Omega\).
The velocity of propagation in a lossless coaxial line having uniform medium is the same as that for a plane wave in the medium, i.e. \(v_{g} = c/\sqrt{\varepsilon_{r}}\). There is one caveat. This is true for all transmission line structures supporting the minimum variation of the fields corresponding to a TEM mode. Higher-order modes, with greater spatial variations of the fields will travel more slowly (i.e. \(v_{g} < c/\sqrt{\varepsilon_{r}}\)), will be considered in Chapter 4. The diameter of the outer conductor and the type of internal supports for the internal conductor determines the frequency range of coaxial components. At high frequencies, and hence short wavelengths, large internal dimensions of a large diameter cable can support more than one spatial variation of the EM fields, i.e. more than one mode. This is undesirable because two modes will travel at different speeds and a propagating signal divides energy between the two modes and, since the modes have different group velocities, the signal will become garbled. Thus the transverse dimensions of the cable determine its upper frequency limit for reliable signal transmission.
There are various coaxial lines with different diameters and different levels of attention given to the uniformity of the lines. Each type of line is called a series and it is necessary to convert between series using adaptors. Various adaptors are shown in Figure \(\PageIndex{3}\). Primarily these have different cost, loss, and uniformity of \(Z_{0}\). It is often necessary to convert between series and also to convert between the sexes (male and female) of connectors. Note that a plug (or jack) could be either female or male.
The different construction of connectors can be seen in Figure \(\PageIndex{4}\). With the APC-7 connector shown in Figure \(\PageIndex{4}\)(a) the inside diameter of the outer conductor is \(7\text{ mm}\). The unique feature of this connector is that it is sexless, with the interface plate being spring-loaded. That is, an APC-7 connector can always be connected to another APC-7 connector. These are precision

Figure \(\PageIndex{4}\): Various coaxial \(50\:\Omega\) transmission line connectors: (a) APC-7 coaxial connector (\(7\text{ mm}\) outer conductor diameter); (b) female N-type (N(f)) coaxial connector (\(7\text{ mm}\)); (c) male SMA-type (SMA(m)) coaxial connector (\(3.5\text{ mm}\)); (d) DC to \(26\text{ GHz}\), 2-W SMA precision fixed attenuator; and (e) N-type inline \(500\text{ MHz}\) lowpass filter. ((d) and (e) copyright 2012 Scientific Components Corporation d/b/a Mini-Circuits, used with permission [4]).

Figure \(\PageIndex{5}\): Coaxial lines: (a) SMA cables (from the top): flexible cable type I, type II, type III, and semirigid cable; (b) coaxial cables showing layers; (c) semirigid coaxial cable bender; (d) bender with line; and (e) hand-formable cable supporting tight radius with low return and insertion loss. ((b) Copyright Megaphase LLC, used with permission [5].) ((e) Copyright 2012 Scientific Components Corporation d/b/a Mini-Circuits, used with permission [4].)
connectors used in some microwave measurements. The N-type connector in Figure \(\PageIndex{4}\)(b) and the SMA connector in Figure \(\PageIndex{4}\)(c) are more common day-to-day connectors. Different views of these connectors are shown in Figures \(\PageIndex{4}\)(d and e). Unlike an APC-7 connector, an N-type (or SMA) male connector, for example, can only be connected to a female N-type connector. There are a large number of different types or series of connectors for highpower applications, different frequency ranges, distortion levels, and cost.
There are also many types of coaxial cables, as shown in Figure \(\PageIndex{5}\)(a). These are cables with SMA connectors (with \(3.5\text{ mm}\) outer conductor diameter). Microwave cables without connectors are shown in Figure \(\PageIndex{5}\)(b). These cables range in cost, flexibility, and the number of times they can be reliably flexed or bent. The semirigid cable shown at the bottom of Figure \(\PageIndex{5}\)(a) must be bent using a bending tool, as shown in Figure \(\PageIndex{5}\)(c), and in

Figure \(\PageIndex{6}\): Torque wrench used in making repeatable coaxial connections. Copyright MegaPhase LLC, used with permission [5].
use in Figure \(\PageIndex{5}\)(d). The controlled bending radius ensures minimal change in the characteristic impedance and propagation constant of the cable. Semirigid cables can only be bent once however. The highest precision bend is realized using an elbow bend, shown in Figure \(\PageIndex{3}\)(g). Various flexible cables have different responses to bending, with higher precision (and more expensive) cables having the least impact on characteristic impedance and phase variations as cables are flexed.
Precision measurements require that connectors be repeatably attached using a torque wrench, as shown in Figure \(\PageIndex{6}\). A torque wrench can be used in a conventional manner, but once the prescribed torque is obtained the wrench breaks just above the head. This ensures that two connectors are repeatably joined with the same force and so the contact resistance and quality of the connection is repeatable.
2.2.7 Microstrip Line
A microstrip line is shown in Figure \(\PageIndex{7}\)(a). This is a commonly used transmission line, as it can be cheaply fabricated using printed circuit board techniques. This line consists of a metal-backed substrate of relative permittivity \(\varepsilon_{r}\) on top of which is a metal strip. Above that is air. The width of the strip determines the characteristic impedance of the line. The characteristic impedance of microstrip lines having various strip widths is shown in Figure \(\PageIndex{8}\) for several substrate permittivities. So the wider the strip and the higher the substrate permittivity, the lower the characteristic impedance of the line. The EM fields are partly in air and partly in the dielectric and an effective permittivity must be used when calculating the electrical length of the line. The results of field simulations of the effective permittivity of lines of various widths and with various substrate permittivities are shown in Figure \(\PageIndex{9}\), where it can be seen that the effective relative permittivity, \(\varepsilon_{e}\), increases for wide strips. This is because more of the EM field is in the substrate. Microstrip transmission line structures are often drawn showing just the layout of the strip, as shown in Figure \(\PageIndex{7}\)(b), where
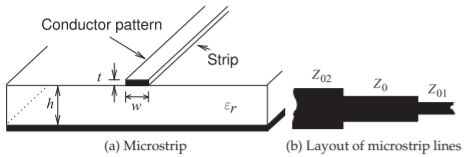
Figure \(\PageIndex{7}\): Microstrip transmission line. The layout (or top) view is commonly used with circuit designs using microstrip. This is the pattern of the strip where (b) shows three lines of different width.
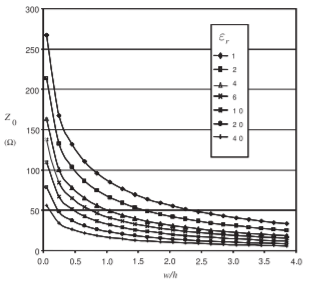
Figure \(\PageIndex{8}\): Dependence of \(Z_{0}\) of a microstrip line at \(1\text{ GHz}\) for various \(\varepsilon_{r}\) and aspect (\(w/h\)) ratios. Calculated using EM simulation.
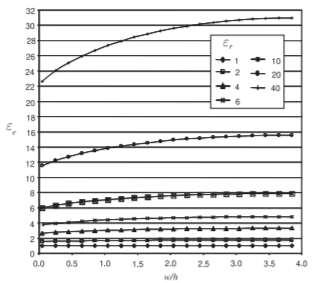
Figure \(\PageIndex{9}\): Dependence of effective relative permittivity \(\varepsilon_{e}\) of a microstrip line at \(1\text{ GHz}\) for various permittivities and aspect ratios (\(w/h\)).
the three lines have different characteristic impedances. The next chapter presents detailed analyses of microstrip and other planar transmission lines.
2.2.8 Summary
The important takeaway from this section is that a signal moves on a transmission line as forward- and backward-traveling waves. The energy transferred is in the traveling waves. The total voltage and current at a point on the line is the sum of the traveling voltage and traveling current waves, respectively, but the total voltage/current view is not sufficient to describe how a transmission line works. Transmission line theory is expressed in terms of traveling voltage and current waves and these are akin to a one-dimensional form of Maxwell’s equations. An argument was developed that posits a model of a line as cascaded sections of RLGC circuit and these circuit elements can be loosely related to the material properties of the medium in which the transmission line is embedded. There are a modification factors due to the actual orientation of the electric and magnetic fields and developing these requires detailed field analysis of the actual transmission line geometry. This can be done for a coaxial line but a microstrip line requires numerical analysis.


