4.2: Frequency-Dependent Characteristics
- Page ID
- 41037
All interconnects have frequency-dependent behavior. In this section the origins of the frequency-dependent behavior of a microstrip line are examined because microstrip has the most significant frequency dependence among interconnects of general interest. Frequency-dependent behavior other than multimoding often results in dispersion. The effect can be seen in Figure 4.1.2 for a pulse traveling along a line. The pulse spreads out as the different frequency components travel at different speeds. For a long line, successive pulses will start merging and the signal will become unintelligible.
The most important frequency-dependent effects are
- changes of material properties (permittivity, permeability, and conductivity) with frequency (Section 4.2.1),
- current bunching (discussed in Section 4.2.3),
- skin effect (Sections 4.2.4 and 4.2.5),
- internal conductor inductance variation (Section 4.2.4),
- dielectric dispersion (Section 4.2.6), and
- multimoding (Section 4.4).
While the discussion focuses on microstrip lines, the effects occur with other planar and nonplanar transmission lines.
4.2.1 Material Dependency
Changes of permittivity, permeability, and conductivity with frequency are properties of the materials used. Fortunately the materials of interest in microwave technology have characteristics that are almost independent of frequency, at least up to \(300\text{ GHz}\) or so.
4.2.2 Frequency-Dependent Charge Distribution
Skin effect, current bunching, and internal conductor inductance are all due to the necessary delay in transferring EM information from one location to another. This information cannot travel faster than the speed of light in the medium. In a dielectric material the speed of an EM wave will be slower
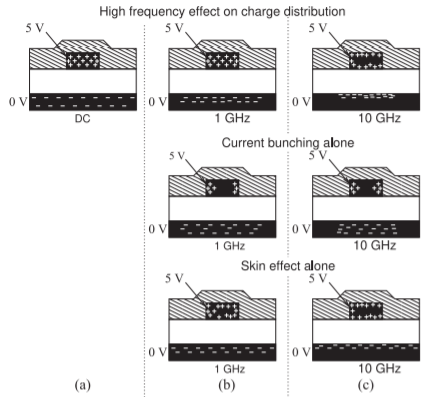
Figure \(\PageIndex{1}\): Cross-sectional view of the charge distribution on an interconnect at different frequencies. The \(+\) and \(−\) indicate charge concentrations of different polarity and corresponding current densities. There is no current bunching or skin effect at DC.
than that in free space by a factor of \(\sqrt{\varepsilon_{r}}\), where \(\varepsilon_{r}\) is the relative permittivity of the material. Thus the speed of an EM wave in microwave dielectrics is reduced typically by a factor ranging from just over \(1\) to \(300\). However, the velocity in a conductor is extremely low because of high conductivity. In brief, current bunching is due to changes related to the finite velocity of information transfer through the dielectric, and skin effect and variations of internal conductor inductance are due to the very slow speed of information transfer inside a conductor. As frequency increases, only limited information to rearrange charges can be sent before the polarity of the signal reverses and information is sent to reverse the changes. The skin and charge-bunching effects on a microstrip line are illustrated in cross section in Figure \(\PageIndex{1}\).
4.2.3 Current Bunching
Consider the charge distribution for a microstrip line shown in the cross-sectional views in Figure \(\PageIndex{1}\). The microstrip cross sections shown here are typical of an interconnect on a printed circuit board or a monolithically integrated circuit where the top dielectric is a passivation layer. The thickness of the microstrip is often a significant fraction of its width, although this is exaggerated in Figure \(\PageIndex{1}\).
The charge distribution shown in Figure \(\PageIndex{1}\)(a) applies when there is a positive DC voltage on the strip (the top conductor). In this case there are positive charges on the top conductor arranged with a fairly uniform distribution. The individual positive charges (caused by the absence of balancing electrons exposing positively charged ions) tend to repel each other, but this has little effect on the charge distribution for practical conductors with finite conductivity. (If the conductor had zero resistance then these net charges would be confined to the surface of the conductor.) The bottom conductor is known as the ground plane and there are balancing
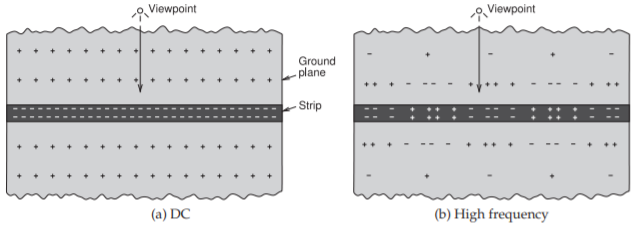
Figure \(\PageIndex{2}\): Current bunching effect in time. Positive and negative charges are shown on the strip and on the ground plane. The viewpoint is on the ground plane.
negative charges, or a surplus of electrons, so that electric field lines begin on the positive charges and terminate on the negative charges. The negative charges on the ground plane are uniformly distributed across the whole of the ground plane. An important point is that where there are unbalanced charges there can be current flow. So the charge distribution at DC, shown in Figure \(\PageIndex{1}\)(a), indicates that for the top conductor, current would flow uniformly inside the conductors and the return current in the ground plane would be distributed over the whole of the ground plane.
The charge distribution becomes less uniform as frequency increases and eventually the signal changes so quickly that information to rearrange charges on the ground plane is soon (half a period latter) countered by reverse instructions. Thus the charge distribution depends on how fast the signal changes. Another way of looking at this effect is to view the charges on the strip of the microstrip line at one time. This is shown in Figure \(\PageIndex{2}\) for a DC signal on the line and for a high-frequency signal. The DC situation is shown in Figure \(\PageIndex{2}\)(a) where there is a uniform distribution of negative charges on the strip. This uniform distribution (in this case of negative charges) is seen from the viewpoint shown. The field then induces uniformly distributed positive charges on the ground plane. At a high frequency the charges on the strip alternate between negative and positive charges, as shown in Figure \(\PageIndex{2}\)(b). Now the effective charge on the strip that is “seen” depends on how far the viewpoint is from the strip. When the viewpoint is at a large distance, it will seem as though the positive and negative charges cancel each other out. Thus on the ground plane at a large distance from the strip there will effectively be very little net charge on the strip. Consequently, at distance, there will be few matching charges on the ground plane that match the charges on the strip. Closer into the strip the ground will “see” a more concentrated charge on the strip and the charges on the ground plane will correspond more closely to the DC situation.
The electric field lines, which must originate and terminate on charges, will concentrate in the substrate more closely under the strip as frequency increases. There will be fewer electric field lines in the air that go out to the fewer distant charges in the ground plane. The two major effects are that the effective permittivity of the microstrip line increases with frequency, and resistive loss increases as the average current density in the ground, which corresponds to the net charge density, increases. Thus the line resistance and capacitance increase with frequency (see Figure 4.1.1(a) and 4.1.1(d), respectively). For the majority of substrates \(G\) is due to dielectric relaxation rather than conduction in the dielectric. As such, \(G\) increases linearly with frequency with a superlinear increase at very high frequencies when the electric field is more concentrated in the dielectric (see Figure 4.1.1(c)).
In the frequency domain the current bunching effects are seen in the higher-frequency views shown in Figures \(\PageIndex{1}\)(b and c). (The concentration of charges near the surface of the metal is a separate effect known as the skin effect.) The longitudinal impact of current or charge bunching alone is illustrated in Figures \(\PageIndex{3}\), \(\PageIndex{4}\), and \(\PageIndex{5}\). These figures present amplitudes of the current and charge phasors at various frequencies and were calculated using the Sonnet EM simulator. In interpreting these figures, take into account the magnitudes of the current and charge distributions as identified in the captions, as the scales are normalized. An alternative view (or time-domain view) is the instantaneous snapshot of current and charge shown in Figure \(\PageIndex{6}\).
This situation is not just confined to the transverse plane, and regions further along the interconnect also send instructions. The net effect is bunching of charges and hence of current on both the ground plane and the strip.
4.2.4 Skin Effect and Internal Conductor Inductance
At low frequencies, currents are distributed uniformly throughout a conductor. Thus there are magnetic fields inside the conductor and hence magnetic energy storage. As a result, there is internal conductor inductance. Transferring charge to the interior of conductors is particularly slow, and as the frequency of the signal increases, charges are confined closer to the surface of the metal. This effect is seen in Figure \(\PageIndex{7}\) where the current density inside the strip of a microstrip line is plotted at various frequencies. Thus time-varying EM fields are not able to penetrate the conductors as much as frequency increases. This phenomenon is known as the skin effect. With lower internal currents, the internal conductor inductance reduces and the total inductance of the line drops [1, 2, 3, 4]. Thus the redistribution of the current results in a change of the inductance with frequency (see Figure 4.1.1(b)). Only above a few gigahertz or so can the line inductance be approximated as a constant for the transverse interconnect dimensions of a micron to several hundred microns.
The skin effect is characterized by the skin depth, \(\delta_{s}\), which is the distance at which the electric field, or equivalently the charge density, reduces to \(1/\text{e}\) of its value at the surface. The skin depth is determined to be
\[\label{eq:1}\delta_{s}=1/\sqrt{\pi f\mu_{0}\sigma_{2}} \]
Here \(f\) is frequency and \(\sigma_{2}\) is the conductivity of the conductor. The conductivity is a measured quantity that is determined by the same physical phenomenon.\(^{1}\) The permittivity and permeability of metals typically used
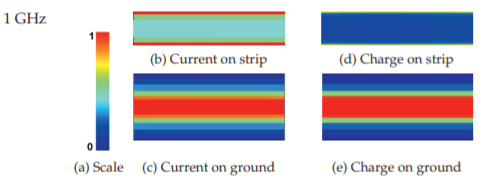
Figure \(\PageIndex{3}\): Normalized current and charge magnitudes on an alumina microstrip line at \(1\text{ GHz}\) (\(\varepsilon_{r} = 10.0\)): (a) scale; (b) longitudinal current, \(i_{z}\), on the strip (\(10–26\text{ A/m}\)); (c) on the ground plane (\(0–3.2\text{ A/m}\)); (d) charge on the strip (\(80–400\text{ nC/m}^{2}\)); and (e) on the ground (\(0–33\text{ nC/m}^{2}\)). See inside the back cover for a color image.
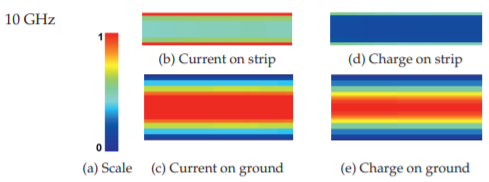
Figure \(\PageIndex{4}\): Normalized current and charge magnitudes on an alumina microstrip line at \(10\text{ GHz}\): (a) scale; (b) longitudinal current, \(i_{z}\), on the strip (\(10–28\text{ A/m}\)); (c) on the ground plane (\(0– 4.1\text{ A/m}\)); (d) charge on the strip (\(114–512\text{ nC/m}^{2}\)); and (e) on the ground (\(0–39\text{ nC/m}^{2}\)). See inside the back cover for a color image.
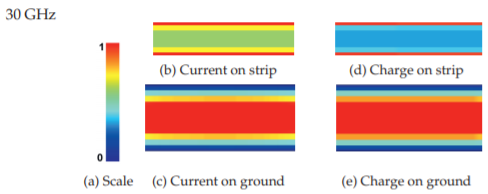
Figure \(\PageIndex{5}\): Normalized magnitudes of current and charge on an alumina microstrip line at \(30\text{ GHz}\): (a) scale; (b) longitudinal current, \(i_{z}\), on the strip (\(10–31\text{ A/m}\)); (c) on the ground plane (\(0–6\text{ A/m}\)); (d) the charge on the strip (\(200–575\text{ nC/m}^{2}\)); and (e) on the ground (\(0–68\text{ nC/m}^{2}\)). See inside the back cover for a color image.
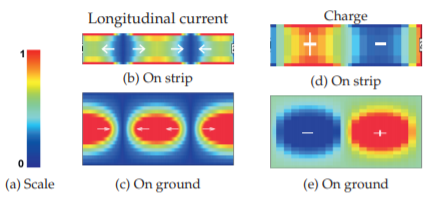
Figure \(\PageIndex{6}\): Normalized instantaneous current and charge on an alumina microstrip line at \(30\text{ GHz}\). Lighter regions have higher current density in (b) and (c), and more positive charge in (d) and (e).
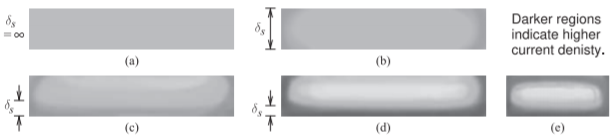
Figure \(\PageIndex{7}\): Cross sections of the strip of a microstrip line showing the impact of skin effect and current bunching on current density: (a) at dc (uniform current density); (b) the strip thickness, \(t\), is equal to the skin depth, \(\delta_{s}\) (i.e. at a low microwave frequency); (c) \(t = 3\delta_{s}\); (d) \(t = 5\delta_{s}\) (i.e. at a high microwave frequency); and (e) \(t = 5\delta_{s}\) for a narrow strip. The plots are the result of 3D simulations of a microstrip line using internal conductor gridding.
for interconnects (e.g., gold, silver, copper, and aluminum) are that of free space, \(\varepsilon_{0}\) and \(\mu_{0}\), respectively, as there is no mechanism to store electric energy (there is no separation of charge centers) and, except for magnetic materials, no mechanism to store magnetic energy (no unbalanced magnetic moments).
4.2.5 Skin Effect and Line Resistance
The skin effect is illustrated in Figure \(\PageIndex{1}\)(b) at \(1\text{ GHz}\). The situation is more extreme as the frequency continues to increase (e.g., to \(10\text{ GHz}\)) as in Figure \(\PageIndex{1}\)(c). There are several important consequences of this. On the top conductor, as frequency increases, current flow is mostly concentrated near the surface of the conductors and the effective cross-sectional area of the conductor, as far as the current is concerned, is less. Thus the resistance of the top conductor increases. A more dramatic situation exists for the charge distribution in the ground plane. From the previous discussion of current bunching it was noted that charge is not uniformly distributed over the whole of the ground plane, but instead becomes more concentrated under the strip as frequency increases. In addition to this, charges and current are confined to the skin of the ground conductor so that the frequency-dependent relative change of ground plane resistance with increasing frequency is greater than that of the strip. On the strip, current bunching results in charges being concentrated on the edges of the strip. This effect is more pronounced the higher the permittivity of the substrate.
The skin effect and current bunching result in frequency dependence of the line resistance, \(R\), with
\[\label{eq:2}R(f)=\left\{\begin{array}{ll}{R(0)}&{f\text{ such that }t\leq 3\delta_{s}}\\{R(0)+R_{\text{skin}}(f)}&{f\text{ such that }t>3\delta_{s}}\end{array}\right. \]
where \(R(0) = R_{\text{strip}}(0) + R_{\text{ground}}(0)\) is the resistance of the line at low frequencies (see Equation (3.5.20)). \(R(f)\) describes the frequency-dependent line resistance that is due to both the skin effect and current bunching. Approximately,
\[\label{eq:3}R_{\text{skin}}(f)=R(0)k\sqrt{f} \]
Here \(k\) is a constant, and while Equation \(\eqref{eq:3}\) indicates proportionality to \(\sqrt{f}\), this is an approximation, but \(R(f)\) always increases more slowly than frequency [4, 6, 7, 8]. The dominant breakpoint is indicated in Equation \(\eqref{eq:2}\).
The increased resistance of the strip at high frequencies results from both current bunching, increasing the current density at the edges of the strip and reducing it in the middle with respect to the width of the strip, and skin effect, increasing the current density on the top and bottom surfaces of the strip and reducing it in the middle with respect to the thickness of the strip (this is of concern at frequencies where \(t > 3\delta_{s}\) [4, 7]). At low frequencies the contribution of the ground to the resistance of the line is small, but because of current bunching the resistance of the ground becomes significant [8] at higher frequencies. The resistance of the ground further increases because of the skin effect and at high microwave frequencies the resistance of the ground can be comparable to that of the strip. Surface roughness of the metal also affects line resistance [9]. This is easy to imagine if the roughness is comparable to the skin depth as the current path is increased by the roughness. Roughness of the metal surface primarily reflects the roughness of the substrate for hard substrates. With soft substrates the underside of the metal is intentionally roughened so that the rough needle-like metal surface penetrates into and anchors to the dielectric when the metal and dielectric are pressed together. For these reasons it is not possible to develop a simple and accurate expression for the frequency-dependent resistance of a microstrip line, and EM simulation is also necessary, but even then roughness cannot be accounted for. EM simulation is necessary in any case to determine attenuation due to radiation. It is essential to incorporate measurements into the design cycle of circuits at high microwave frequencies to account for effects that cannot be modeled [10, 11]. One observation on the frequency dependence of resistance is that it is pointless to make the thickness of the strip or of the ground thicker than three times the skin depth.
Determine the skin depth for copper (Cu), silver (Ag), aluminum (Al), gold (Au), and titanium (Ti) at \(100\text{ MHz},\: 1\text{ GHz},\: 10\text{ GHz},\) and \(100\text{ GHz}\).
Solution
The skin depth is calculated using Equation \(\eqref{eq:1}\) and the conductivity from Appendix 2.A.
| Metal | Resistivity \((\text{n}\Omega\cdot\text{m})\) | Conductivity \((\text{MS/m})\) |
Skin depth, \(\delta_{s}\) \((\mu\text{m})\) | |||
|---|---|---|---|---|---|---|
| \(100\text{ MHz}\) | \(1\text{ GHz}\) | \(10\text{ GHz}\) | \(100\text{ GHz}\) | |||
| Copper (Cu) | \(16.78\) | \(59.60\) | \(6.52\) | \(2.06\) | \(0.652\) | \(0.206\) |
| Silver (Ag) | \(15.87\) | \(63.01\) | \(6.34\) | \(2.01\) | \(0.634\) | \(0.201\) |
| Aluminum (Al) | \(26.50\) | \(37.74\) | \(8.19\) | \(2.59\) | \(0.819\) | \(0.259\) |
| Gold (Ag) | \(22.14\) | \(45.17\) | \(7.489\) | \(2.37\) | \(0.749\) | \(0.237\) |
| Titanium (Ti) | \(4200\) | \(0.2381\) | \(103.1\) | \(32.6\) | \(10.3\) | \(3.26\) |
Table \(\PageIndex{1}\)
4.2.6 Dielectric Dispersion
Dispersion is principally the result of the propagation velocity of a sinusoidal signal being dependent on frequency. For a pulse on the line, dispersion manifests as the various frequency components of a signal traveling with different velocities.
The electric field lines shift as a result of the different distributions of charge, with more of the electric energy being in the dielectric as frequency increases. Thus the effective permittivity of a microstrip line increases with increasing frequency. At high frequencies, the fundamental result of the field rearrangement is that the capacitance of the line increases, but this change can be quite small—typically less than \(10\%\) over the range of DC to \(100\text{ GHz}\). (This effect is described by the frequency dependence of the effective permittivity of the transmission line.) To a lesser extent, dispersion is also the result of other transmission line parameters changing with frequency, such as an interconnect’s resistance. For an IC where the interconnects can have very small transverse dimensions (e.g., microns) on digital ICs, the line resistance is the most significant source of dispersion. The qualitative effect of dispersion is the same whether it is related to the resistance (resistance-induced dispersion) or change in the effective permittivity (dielectric-inhomogeneity-induced dispersion).
Different interconnect technologies have different dispersion characteristics. For example, with a microstrip line the effective permittivity changes with frequency as the proportion of the EM energy in the air region to that in the dielectric region changes. Dispersion is reduced if the fields are localized and cannot change orientation with frequency. This is the case with coplanar interconnects—in particular, coplanar waveguide (CPW) and coplanar strip (CPS) lines. The stripline of Figure 3.3.1(k) also has low dispersion, as the fields are confined in one medium and the effective permittivity is just the permittivity of the medium. Thus interconnect choices can have a significant effect on the integrity of a signal being transmitted.
As discussed earlier, as the frequency is increased, the fields on a microstrip line become more concentrated in the region beneath the strip. Thus there is a frequency-dependent effective microstrip permittivity, \(\varepsilon_{e}(f)\). This quantity increases with frequency and the wave is progressively slowed down. The effective microstrip permittivity is now
\[\label{eq:4}\varepsilon_{e}(f)=\{c/[v_{p}(f)]\}^{2} \]
Fundamentally, characterizing the dispersion problem then consists of solving the transmission line fields for the frequency-dependent phase velocity, \(v_{p}(f)\). The limits of \(\varepsilon_{e}(f)\) are readily established; at the low-frequency extreme it reduces to the static TEM value \(\varepsilon_{e}\) (or \(\varepsilon_{e}(0)\)), while as frequency is increased indefinitely, \(\varepsilon_{e}(f)\) approaches the substrate permittivity itself, \(\varepsilon_{r}\). That is,
\[\label{eq:5}\varepsilon_{e}(f)\to\left\{\begin{array}{ll}{\varepsilon_{e}(0)}&{\text{as }f\to 0}\\{\varepsilon_{r}}&{\text{as }f\to\infty}\end{array}\right. \]
Between these limits \(\varepsilon_{e}(f)\) changes smoothly.
4.2.7 Summary
Various transmission line technologies have different frequency dispersion characteristics. The two most important technologies for microwave circuits are coaxial lines and microstrip. With both the variation of resistance with frequency due principally to the skin effect are significant. However this has little effect on characteristic impedance and effective permittivity with the dominate effect being increased loss at higher frequencies. With microstrip, but not with a coaxial line, variations due to changing orientation of the EM fields is the most significant effect. With increasing frequency the proportion of signal energy in the air region reduces and the proportion in the dielectric increases. The overall trend with microstrip is for the fields to be more concentrated in the dielectric as frequency increases and this increases a microstrip line’s effective relative permittivity and hence slows down propagation. The variation of characteristic impedance of microstrip with frequency is more complex as the increasingly tight transverse rotation, i.e. curl, of the fields tends to increase characteristic impedance but the increasing effective permittivity tends to decrease characteristic impedance. Thus following the initial design of a microstrip circuit, it is important to use EM simulations to adjust designs to account for dispersion.
Footnotes
[1] This phenomenon is described by M. Born and E. Wolf [5]. In a conductor an electric field accelerates free electrons that in turn radiate around the direction of motion. This process is repeated as the field penetrates the conductor. While the leading edge of the electric field propagates quickly through the conductor it rapidly diminishes in amplitude. The average field penetrates very slowly due to the large number of free electrons and multiple scattering of the field. A rough guide is that the effective velocity at microwave frequencies for transfer of the bulk of the energy is about \(c/1000\). It is not possible to determine an accurate number.


