4.13: Exercises
- Page ID
- 41045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Current bunching and the skin effect result in transmission line loss increasing with frequency.
- Show current bunching on a transverse diagram of the microstrip line.
- Describe the skin effect on a transverse diagram of the microstrip line.
- What is the skin depth on a copper microstrip line at \(10\text{ GHz}\)? Assume that the conductivity of the deposited copper forming the strip is half that of bulk single-crystal copper. Use the data in the table on page 130.
- What is the skin depth on a silver microstrip line at \(1\text{ GHz}\)? Assume that the conductivity of the fabricated silver conductor is \(75\%\) that of bulk single-crystal silver. Use the data in the table on page 130.
- What is the dominant source of dispersion on a microstrip transmission line?
- Using Figure 4.3.3, determine the complex characteristic impedance and complex effective permittivity of a microstrip line at \(12\text{ GHz}\). The line is fabricated on alumina with \(\varepsilon_{r}(0) = 9.9,\: w = 240\:\mu\text{m},\: h = 500\:\mu\text{m}\).
- A magnetic wall and an electric wall are \(2\text{ cm}\) apart and are separated by a lossless material having a relative permittivity of \(10\) and a relative permeability of \(23\). What is the cut-off frequency of the lowest-order mode in this system?
- Describe the transverse resonance mode on stripline. When can it occur?
- The strip of a microstrip has a width of \(600\:\mu\text{m}\) and is fabricated on a lossless substrate that is \(1\text{ mm}\) thick and has a relative permittivity of \(10\).
- Draw the microstrip waveguide model of the microstrip line. Put dimensions on your drawing.
- Sketch the electric field distribution of the first transverse resonance mode and calculate the frequency at which the transverse resonance mode occurs.
- Sketch the electric field distribution of the first higher-order microstrip mode and calculate the frequency at which it occurs.
- Sketch the electric field distribution of the slab mode and calculate the frequency at which it occurs.
- A microstrip line has a width of \(352\:\mu\text{m}\) and is constructed on a substrate that is \(500\:\mu\text{m}\) thick with a relative permittivity of \(5.6\).
- Determine the frequency at which transverse resonance would first occur.
- When the dielectric is slightly less than one-quarter wavelength in thickness the dielectric slab mode can be supported. Some of the fields will appear in the air region as well as in the dielectric, extending the effective thickness of the dielectric. Ignoring the fields in the air (use a one-quarter wavelength criterion), at what frequency will the dielectric slab mode first occur?
- The strip of a microstrip has a width of \(600\:\mu\text{m}\) and uses a lossless substrate that is \(635\:\mu\text{m}\) thick and has a relative permittivity of \(4.1\).
- At what frequency will the first transverse resonance occur?
- At what frequency will the first higher-order microstrip mode occur?
- At what frequency will the slab mode occur?
- Identify the useful operating frequency range of the microstrip.
- The design space for transmission lines in microstrip designs is determined by the design project leader to be \(20–100\:\Omega\). The preferred substrate has a thickness of \(500\:\mu\text{m}\) and a relative permittivity of \(8\). What is the maximum operating frequency range of designs supported by this technology choice. Ignore frequency dispersion effects (i.e., frequency dependence of effective permittivity and losses). [Hint: First determine the dimensions of the strip that will provide the required impedance range and then determine the frequency at which lowest-order multimoding occurs.]
- Consider the design of transmission lines in microstrip technology using a lossless substrate with a relative permittivity of \(10\) and thickness of \(400\:\mu\text{m}\). You will want to use the formulas in Section 3.5.3.
- What is the maximum characteristic impedance that can be achieved for a transmission line fabricated in this technology?
- Plot the characteristic impedance versus strip width.
- From manufacturing tolerance considerations, the minimum strip width that can be manufactured is \(20\:\mu\text{m}\). What is the maximum characteristic impedance that can be achieved in practice?
- If the operating frequency range is \(1– 10\text{ GHz}\), determine the maximum width of the strip from higher-order mode considerations. You must consider the transverse resonance mode as well as higher-order microstrip modes.
- Identify the electrical design space (i.e., the achievable characteristic impedance range).
- Identify the physical design space (i.e., the range of acceptable strip widths).
- If the electrical design space requires that transmission line impedances be achieved within \(±2\:\Omega\), what tolerance must be achieved in the manufacturing process if the substrate thickness can be achieved exactly? [Hint: First identify the critical physical process corner and thus the critical strip width that is most susceptible to width variations. Then determine the tolerance on the strip width to achieve the allowable characteristic impedance variation. That is, characteristic impedance is a function of strip width and height. If the substrate is perfect (no height variation), then how much can the strip width vary to keep the impedance within \(±2\:\Omega\) of the desired value? You can solve this graphically using a plot of \(Z_{0}\) versus width or you can iteratively arrive at the answer by recalculating \(Z_{0}\).]
- If the electrical design space requires that transmission line impedances be achieved within \(±2\:\Omega\), what tolerance must be achieved in the manufacturing process if the substrate thickness tolerance is \(±2\:\mu\text{m}\)? If the substrate is not perfect (the height variation is \(±2\:\mu\text{m}\)), then how much can the strip width vary to keep the impedance within \(±2\:\Omega\) of the desired value? This problem is directly applicable to real-world process/design trade-offs.
- The strip of a microstrip has a width of \(500\:\mu\text{m}\) and is fabricated on a lossless substrate that is \(635\:\mu\text{m}\) thick and has a relative permittivity of \(12\). [Parallels Examples 4.6.1, 4.6.2, and 4.6.3]
- At what frequency does the transverse resonance first occur?
- At what frequency does the first higher-order microstrip mode first propagate?
- At what frequency does the substrate (or slab) mode first occur?
- The strip of a microstrip has a width of \(250\:\mu\text{m}\) and uses a lossless substrate that is \(300\:\mu\text{m}\) thick and has a relative permittivity of \(15\).
- At what frequency does the transverse resonance first occur?
- At what frequency does the first higher-order microstrip mode propagate?
- At what frequency does the substrate (or slab) mode first occur?
- What is the highest operating frequency of the microstrip?
- A microstrip line has a strip width of \(100\:\mu\text{m}\) and is fabricated on a substrate that is \(150\:\mu\text{m}\) thick and has a relative permittivity of \(9\).
- Draw the microstrip waveguide model and indicate and calculate the dimensions of the model.
- Based only on the microstrip waveguide model, determine the frequency at which the first transverse resonance occurs?
- Based on the microstrip waveguide model, determine the frequency at which the first higher-order microstrip mode occurs?
- At what frequency will the slab mode occur? For this you cannot use the microstrip waveguide model.
- A microstrip line has a strip width of \(100\:\mu\text{m}\) and is fabricated on a substrate that is \(150\:\mu\text{m}\) thick and has a relative permittivity of \(9\).
- Define the properties of a magnetic wall.
- Identify two situations where a magnetic wall can be used in the analysis of a microstrip line; that is, give two situations where a magnetic wall approximation can be used.
- Draw the microstrip waveguide model and indicate and calculate the dimensions of the model.
- Consider the design of transmission lines in microstrip technology using a lossless substrate with relative permittivity of \(20\) and thickness of \(200\:\mu\text{m}\).
- Using qualitative arguments, show that the maximum characteristic impedance that can be achieved for a transmission line fabricated in this technology is \(116\:\Omega\). The maximum is not actually \(116\:\Omega\), but a simple argument will bring you to this conclusion.
- Plot the characteristic impedance versus substrate width.
- From manufacturing tolerance considerations, the minimum strip width that can be manufactured is \(20\:\mu\text{m}\). What is the maximum characteristic impedance that can be achieved in practice?
- If the operating frequency range is \(2– 18\text{ GHz}\), determine the maximum width of the strip from higher-order mode considerations. You must consider the transverse resonance mode, the higher-order mode, and the slab mode.
- Identify the electrical design space (i.e., the characteristic impedance range).
- Identify the physical design space (i.e., the range of acceptable strip widths).
- If the electrical design space requires that transmission line impedances be achieved within \(±2\:\Omega\), what tolerance must be achieved in the manufacturing process if the substrate thickness can be achieved exactly? [Hint: First identify the critical physical process corner and thus the critical strip width that is most susceptible to width variations. Then determine the tolerance on the strip width to achieve the allowable characteristic impedance variation.]
- If the electrical design space requires that transmission line impedances be achieved within \(±2\:\Omega\), what tolerance must be achieved in the manufacturing process if the substrate thickness tolerance is \(±2\:\mu\text{m}\)?
- The strip of a microstrip line has a width of \(0.5\text{ mm}\), and the microstrip substrate is \(1\text{ mm}\) thick and has a relative permittivity of \(9\) and relative permeability of \(1\).
- Draw the microstrip waveguide model and calculate the dimensions of the model. Clearly show the electric and magnetic walls in the model.
- Use the microstrip waveguide model to calculate the cut off frequency of the transverse resonance mode?
- A substrate mode can also be excited but the cut off frequency of this mode cannot be calculated using the microstrip waveguide model. Provide a brief description of the substrate mode and calculate the lowest frequency at which it can exist.
- A microstrip technology uses a substrate with a relative permittivity of \(10\) and thickness of \(400\:\mu\text{m}\). If the operating frequency is \(10\text{ GHz}\), what is the maximum width of the strip from higher-order mode considerations.
- A microstrip line operating at \(18\text{ GHz}\) has a \(200\:\mu\text{m}\) thick substrate with a relative permittivity of \(20\).
- Determine the maximum width of the strip from higher-order mode considerations. Consider the transverse resonance mode, the higher-order microstrip mode, and the slab mode.
- Thus determine the minimum achievable characteristic impedance.
- A microstrip line has a strip width of \(100\:\mu\text{m}\) and is fabricated on a \(150\:\mu\text{m}\)-thick lossless substrate with a relative permittivity of \(9\).
- Define the properties of a magnetic wall.
- Identify two situations where a magnetic wall can be used in determining multimoding on a microstrip line. That is, give two locations where a magnetic wall approximation can be used.
- Two magnetic walls are separated by \(1\text{ mm}\) in a lossless material having a relative permittivity of \(9\) and a relative permeability of \(1\).
- What is the wavelength of a \(10\text{ GHz}\) signal in this material?
- Now consider a field variation, i.e. a mode and not constant, established by the magnetic walls. Describe this lowest order field variation. That is how does the \(\text{H}\) field vary or how does the \(\text{E}\) field vary (one is sufficient)?
- What is the lowest frequency at which a field variation can be supported by those walls in the specified medium?
- A microstrip line has a strip width of \(250\:\mu\text{m}\) and a \(300\:\mu\text{m}\) thick substrate with a relative permittivity of \(15\). At what frequency can the substrate mode first occur?
- A microstrip line has a strip width of \(250\:\mu\text{m}\) and a \(300\:\mu\text{m}\) thick substrate with a relative permittivity of \(15\). At what frequency can a higher-order microstrip mode first propagate?
- A microstrip line has a strip width of \(200\:\mu\text{m}\) and a substrate that is \(400\:\mu\text{m}\) thick and has a relative permittivity of \(4\). Use the microstrip waveguide model to determine the lowest frequency at which higher-order microstrip mode can occur.
- A microstrip line has a strip width of \(250\:\mu\text{m}\) and a \(300\:\mu\text{m}\) thick substrate with a relative permittivity of \(15\). At what frequency can transverse resonance first occur?
- The figure below is the cross section of a finite ground coplanar waveguide (FGCPW) transmission line over a ground plane. The FGCPW consists of the ground strips of width \(w_{1}\) and the strip of width \(w\). Now \(w_{1} = 2.5\times s,\: w = 1.3\times s,\) and \(h = 4\times s\). The thickness is \(t = 0.3\times s\).
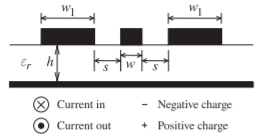
Figure \(\PageIndex{1}\)
- Ignore the bottom ground plane for now. Redraw the structure and indicate the charge and current distributions at microwave frequencies using the convention shown. On the strip the current flows in and the charge is positive.
- Does this structure support a transverse EM mode?
- Again ignoring the bottom ground plane, redraw the structure and indicate the region where the energy is concentrated.
- Now consider the complete structure. If the guide wavelength is \(\lambda_{g}\), and the wavelength in the dielectric is \(\lambda\), indicate the criterion for the lowest frequency at which transverse resonance will become a problem.
- Use a diagram to show the \(E\) and \(H\) fields of the microstrip mode on finite ground CPW.
- Does finite ground CPW support a transverse resonance mode? Explain.
- For a finite ground CPW line illustrate the following modes and the conditions under which they occur.
- The microstrip mode.
- The cross mode (the ground planes not at the same potential).
- The transverse mode mode.
- Consider a symmetrical stripline with the following parameters: total substrate thickness, \(d = 1.7\text{ mm}\); strip width, \(w = 2.5\text{ mm}\); relative permittivity of the substrate \(= 9\); and operating frequency \(= 30\text{ GHz}\).
- What is the value of the effective permittivity?
- What is the value of the free-space wavelength?
- What is the value of the guide wavelength?
- What is the dominant cause of dispersion on a stripline? That is, what is most likely to cause frequency dependence of the characteristic impedance and propagation constant of the line.
- The strip of a microstrip line has a width of \(200\:\mu\text{m}\) and the substrate is \(400\:\mu\text{m}\) thick and has a relative permittivity of \(4\).
- Draw the effective waveguide model of a microstrip line with magnetic walls and an effective strip width, \(w_{\text{eff}}\).
- What is the effective relative permittivity of the microstrip waveguide model?
- What is \(w_{\text{eff}}\)?
- Can the lowest frequency at which the transverse resonance mode first occurs be determined from the microstrip waveguide model?
- The strip of a symmetrical stripline has a width of \(200\:\mu\text{m}\) and is embedded in a lossless medium that is \(400\:\mu\text{m}\) thick and has a relative permittivity of \(13\), thus the separation, \(h\), from the strip to each of the ground planes is \(200\:\mu\text{m}\).
- Draw the waveguide model of a stripline with magnetic walls and an effective strip width, \(w_{\text{eff}}\), which will be approximately the same as with a microstrip line.
- What is the effective relative permittivity of the stripline waveguide model?
- What is \(w_{\text{eff}}\)?
- At what frequency will the first transverse resonance occur?
- At what frequency will the first higher-order stripline mode occur?
- At what frequency will the first parallel-plate waveguide mode occur? Do not consider the mode with no field variation, as this cannot be excited.
- Identify the useful operating frequency range of the stripline.
- Describe the parallel-plate mode on stripline.
- Consider the structure in Figure 4.10.2. Determine the guide wavelength, \(\lambda_{g}\), and the wavelength in the top insulator, \(\lambda_{1}\), at a frequency of \(20\text{ GHz}\). The permittivities are \(\varepsilon_{1} = 3.9\varepsilon_{0}\) and \(\varepsilon_{2} = 13\varepsilon_{0}\). The depths of the dielectrics are \(d_{2} = 100\:\mu\text{m}\) and \(d_{1} = 1.0\:\mu\text{m}\). [Parallels Example 4.10.1]
- Consider a metal-oxide-semiconductor transmission medium as examined in Section 4.10. The structure in the form of a Maxwell–Wagner capacitor is shown in Figure 4.10.3(a) with \(d_{1} = 100\:\mu\text{m},\: d_{2} = 500\:\mu\text{m}\), and relative permittivities \(\varepsilon_{r1} = 3.9\) and \(\varepsilon_{r2} = 13\). Ignore the finite conductivity. What is the capacitance model of this structure (see Figure 4.10.3(b)) and what are the values of the capacitances?
4.13.1 Exercises by Section
\(†\)challenging, \(‡\)very challenging
\(§4.2\: 1†, 2, 3\)
\(§4.3\: 4†\)
\(§4.4\: 5\)
\(§4.5\: 6, 7 \)
\(§4.6\: 8†, 9†, 10†, 11‡, 12‡, 13†, 14†, 15†, 16†, 17‡, 18†, 19, 20, 21, 22, 23, 24, 25, 26\)
\(§4.7\: 27‡, 28, 29, 30\)
\(§4.8\: 31‡, 32†, 33†, 34‡, 35\)
\(§4.10\: 36, 37†\)
4.13.2 Answers to Selected Exercises
- \(2.315\:\mu\text{m}\)
- \(247\text{ MHz}\)
- (c) \(25\text{ GHz}\)
- (c) \(\text{DC}\) to \(63.4\text{ GHz}\)
- (d) \(\text{DC}\leq f\leq 48.6\text{ GHz}\)
- \(104.6\text{ GHz}\)
- (a) \(116\:\Omega\)
- (f) \(20\:\mu\text{m}<w<1.96\text{ mm}\)
- (b) \(55.6\text{ GHz}\)
- \(207.9\text{ GHz}\)


