6.14: Exercises
- Page ID
- 46138
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- A mixer has an LO at \(28.2\text{ GHz}\). The mixer is used to convert a signal at \(28.1\text{ GHz}\) to an IF at \(100\text{ MHz}\), and has a conversion loss of \(13\text{ dB}\) and an image rejection of \(40\text{ dB}\). Two signals are presented to the mixer, one at \(28.1\text{ GHz}\) with a power of \(1\text{ pW}\) and the other at \(28.3\text{ GHz}\) with a power of \(10\:\mu\text{W}\). [Parallels Example 6.2.1]
- What is the power of the (intended) signal at the IF in \(\text{dBm}\)?
- What is the signal-to-interference ratio at the IF (ignoring noise)?
- Consider the single-ended diode mixer in Figure 6.2.5(a).
- Develop a symbolic expression for the voltage at the test point. The diode is modeled by \(i_{D} = a_{1}v_{D} + a_{2}v^{2}_{D} + a_{3}v^{3}_{D}\).
- What are the frequencies and amplitudes of the components of the spectrum at the test point?
- A mixer in a receiver has a conversion loss of \(16\text{ dB}\). If the applied RF signal has an available power of \(100\:\mu\text{W}\), what is the available power of the IF at the output of the mixer?
- The RF signal applied to the input of a mixer has a power of \(1\text{ nW}\) and the output of the mixer at the IF has a power level of \(100\text{ pW}\). What is the conversion loss of the mixer in decibels?
- A mixer in a receiver has a conversion gain of \(10\text{ dB}\). If the applied RF signal has a power of \(100\:\mu\text{W}\), what is the available power of the IF at the output of the mixer?
- A mixer in a receiver has a conversion loss of \(6\text{ dB}\). If the applied RF signal has a power of \(1\:\mu\text{W}\), what is the available power of the IF at the output of the mixer?
- A mixer has an LO at \(18\text{ GHz}\). The mixer is used to convert a signal at \(18.5\text{ GHz}\) to an IF at \(500\text{ MHz}\). Two signals are presented to the mixer, one at \(18.5\text{ GHz}\) with a power of \(100\text{ nW}\) and an interfering signal at \(17.5\text{ GHz}\) with a power of \(10\text{ nW}\). If the image rejection is \(20\text{ dB}\) and the conversion loss is \(10\text{ dB}\).
- What is the signal power at the IF?
- What is the interference power at the IF?
- What is the signal-to-interference ratio (in decibels) at the IF?
- A mixer has an LO at \(100\text{ GHz}\). The mixer is used to convert a signal at \(110\text{ GHz}\) to an IF at \(10\text{ GHz}\). Two signals are presented to the mixer, one at \(110\text{ GHz}\) with a power of \(10\text{ nW}\) and an interfering signal at \(90\text{ GHz}\) with a power of \(5\text{ nW}\). If the image rejection is \(40\text{ dB}\) and the conversion loss is \(20\text{ dB}\), what is the signal-to-interference ratio (in decibels) at the IF?
- A mixer has an LO at \(18\text{ GHz}\). The mixer is used to convert a signal at \(18.5\text{ GHz}\) to an IF at \(500\text{ MHz}\). The RF signal at \(18.5\text{ GHz}\) has a power of \(100\text{ pW}\). In addition, noise with a power of \(1\text{ pW}\) is applied to the mixer at \(18.5\text{ GHz}\) and \(17.5\text{ GHz}\) (\(1\text{ pW}\) at \(18.5\text{ GHz}\) and \(1\text{ pW}\) at \(17.5\text{ GHz}\)). If the image rejection is \(6\text{ dB}\) and the conversion loss is \(10\text{ dB}\). Ignore noise contributions from the mixer. What is the SNR (in decibels) at the IF?
- A mixer in a communication system has an LO at \(5.5\text{ GHz}\). The mixer is used to convert a \(10\text{ MHz}\) bandwidth signal at \(5.6\text{ GHz}\) to an IF at \(100\text{ MHz}\). The RF signal at \(5.6\text{ GHz}\) has a power of \(100\text{ pW}\). The image rejection is ideal and the conversion loss is \(10\text{ dB}\). The mixer has a single-sideband noise figure of \(6\text{ dB}\).
- What is the noise power at the input if the source is held at standard temperature (\(290\text{ K}\))?
- What is the input SNR (in decibels)?
- What is the SNR (in decibels) at the IF?
- The double-balanced ring diode mixer shown below has the special characteristic that the LO and RF tones are suppressed at the IF output port. Develop a symbolic expression for the voltage at the IF port. The diodes are matched and are modeled by \(i_{D} = a_{1}v_{D} + a_{2}v^{2}_{D} + a_{3}v^{3}_{D}\). The LO voltage, at the LO terminal, is \(v_{\text{LO}} = A \cos(\omega_{\text{LO}}t)\) and the RF voltage, at the RF terminal, is \(v_{\text{RF}} = B \cos(\omega_{\text{RF}}t)\). Consider a \(1:1\) winding ratio. That is, the number of windings on the secondary on each side of the center tap is equal to the number of windings on the primary.
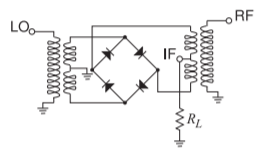
- A diode double-balanced mixer has an LO at \(100\text{ GHz}\) and has an input RF signal of \(101\text{ GHz}\). What will be the frequencies of the main signals at the IF?
- The phase noise of an oscillator was measured as \(−120\text{ dBc/Hz}\) at \(10\text{ kHz}\) offset. What is the normalized phase noise at \(1\text{ MHz}\) offset, assuming that the phase noise power varies as the inverse of frequency?
- The phase noise of an oscillator was measured as \(−130\text{ dBc/Hz}\) at \(10\text{ kHz}\) offset. What is the normalized phase noise at \(1\text{ MHz}\) offset, assuming that the phase noise power varies as the inverse of frequency?
- The phase noise of an oscillator was measured as \(−125\text{ dBc/Hz}\) at \(100\text{ kHz}\) offset. What is the normalized phase noise at \(1\text{ MHz}\) offset, assuming that the phase noise power varies as the square of the inverse of frequency?
- The phase noise of an oscillator was measured as \(−125\text{ dBc/Hz}\) at \(100\text{ kHz}\) offset. What is the normalized phase noise at \(1\text{ MHz}\) offset, assuming that the phase noise power varies inversely with frequency offset?
- When \(0\text{ V}\) is applied to a VCO, the output frequency is \(1\text{ GHz}\). When the input to the VCO is \(10\text{ mV}\), the sinusoidal output of the VCO has a frequency of \(1.01\text{ GHz}\). What is the tuning gain of the VCO?
- If a sinusoidal voltage is applied to the input of an analog VCO, describe the signal at the output of the VCO.
- Describe the design of a times-two frequency divider using a frequency multiplier based on a diode and one or more bandpass filters. That is, sketch the circuit at the block diagram level.
- Describe the design of a times-three frequency divider using a frequency multiplier based on a diode and one or more bandpass filters. That is, sketch the circuit at the block diagram level.
6.14.1 Exercises By Section
\(†\)challenging, \(‡\)very challenging
\(§6.2 1, 2†, 3, 4, 5, 6, 7†, 8†, 9†, 10†\)
\(§6.3 11‡, 12\)
\(§6.4 13†, 14†, 15†, 16\)
\(§6.5 17, 18\)
\(§6.9 19, 20\)
6.14.2 Answers to Selected Exercises
- \(-26\text{ dBm}\)
- \(0\text{ dBm}\)
- (b) \(10\text{ pW}\)
- \(19.0\text{ dB}\)
- (b) \(28\text{ dB}\)
- One signal at \(1\text{ GHz}\)
- \(1\text{ GHz/V}\)

