2.13: Phase Shift Keying Modulation
- Page ID
- 41185
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)There are many variations on phase shift keying (PSK) modulation with the methods differing by their spectral efficiencies, PMEPR, and suitability for carrier recovery. Compared to FSK more sophisticated digital signal processing is required to demodulate a PSK-modulated signal.
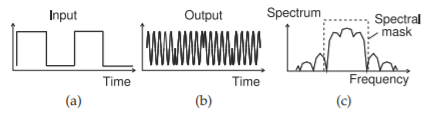
Figure \(\PageIndex{1}\): Binary PSK modulation: (a) modulating bitstream; (b) the modulated waveform; and (c) its spectrum after smoothing the transitions from one phase state to another.
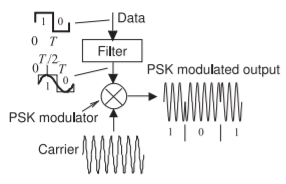
Figure \(\PageIndex{2}\): A binary phase shift keying (PSK) modulation system.
2.8.1 Essentials of PSK
PSK is an efficient digital modulation scheme and can be simply implemented and demodulated using a phase-locked loop. The simplest scheme is binary PSK (BPSK) with two phase states. The waveform and spectrum of BPSK are shown in Figure \(\PageIndex{2}\). The incoming baseband bitstream shown in Figure \(\PageIndex{1}\)(a) modulates the phase of a carrier producing the modulated signal shown in Figure \(\PageIndex{1}\)(b). The spectrum of the modulated signal is shown in Figure \(\PageIndex{1}\)(c). What is very interesting about this spectrum is that it approximately fills a square. So PSK modulation results in an efficient use of the spectrum. This can be contrasted with the spectrum of an FM signal shown in Figure 2.4.5(c), which does not fill the channel uniformly. A binary PSK modulation system is shown in Figure \(\PageIndex{2}\) where the binary input data causes \(180^{\circ}\) phase changes of the carrier. The abrupt changes in phase shown in the output modulated waveform result in more bandwidth than is necessary. However a practical PSK modulator first lowpass filters the binary data before the carrier is modulated. This filtering eliminates the abrupt changes in the phase of the modulated signal and so reduces the required bandwidth. It is the spectrum of this signal that is shown in Figure \(\PageIndex{1}\)(c).
There are many variants of increasing complexity, called orders, of PSK, with the fundamental characteristics being the number of phase states (e.g. with \(2^{n}\) phase states, \(n\) bits of information can be transmitted) and how the phasor of the RF signal transitions from one phase state to another. PSK schemes are designed to shape the spectrum of the modulated signal to fit as much energy as possible within a spectral mask. This results in a modulated carrier whose amplitude varies (and thus has a time-varying envelope). Such schemes require highly linear amplifiers to preserve the amplitude variations of the modulated RF signal.
There are PSK methods that manage the phase transitions to achieve a constant envelope modulated RF signal but these have lower spectral efficiency. Military radios sometimes use this type of modulation scheme as it is much harder to detect and intercept communications if the amplitude of the modulated carrier is constant.
The communication limit of one symbol per hertz of bandwidth,
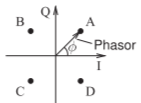
Figure \(\PageIndex{3}\): Phasor diagram of QPSK modulation. Here there are four discrete phase states of the phasor indicated by the points A, B, C, and D. The PSK modulator moves the phasor from one phase state to another. The task at the receiver is determining the phase of the phasor.
the symbol rate, comes from the Nyquist signaling theorem.\(^{1}\) Nyquist determined that the number of independent pulses that could be put through a telegraph channel per unit of time is limited to twice the bandwidth of the channel. With a modulated RF carrier, this translates to the modulated carrier moving from one state to another in a unit of time equal to one over the bandwidth. The transition identifies a symbol, and hence one symbol can be sent per hertz of bandwidth. More accurately it could be said that the transition is a symbol rather than the end of the transition being a symbol. In PSK modulation the states are the phases of a phasor since the amplitude of the modulated signal is (ideally) constant.
The phase-shifted (i.e. phase-modulated) carrier of a PSK signal can be represented on a phasor diagram. Figure \(\PageIndex{3}\) is a phasor diagram with four phase states—A, B, C, D—and the phasor moves from one state to another under the control of the modulation circuit. What is shown here is 4-state PSK or quadra-phase shift keying (QPSK) and very often but less accurately called quadrature phase shift keying. The states, or symbols, are identified by their angle or equivalently by their rectangular coordinates, called I, for in-phase, and Q, for quadrature phase.
PSK Modulation
In PSK modulation the phase of a carrier signal is set to one of a number of discrete values at the clock ticks. For example, in QPSK there are four discrete settings of the phase of the carrier, e.g. \(45^{\circ},\: 135^{\circ},\: −135^{\circ},\) and \(−45^{\circ}\). Converting this to radians the discrete baseband signal is \(\phi (t) = π/4,\: 3π/4,\: 5π/4,\) and \(7π/4\), at the clock ticks. Thus if the bandwidth of the baseband signal is \(1\text{ MHz}\) what is shown as \(\phi(t)\) are the intended phases of the carrier every microsecond. Wave-shaping or filtering is used to provide a smooth variation of \(\phi(t)\) between the clock ticks and so the bandwidth of the modulated signal is constrained. High-order PSK modulation has more discrete states, e.g. 8-PSK has eight discrete phase states.
There are several ways to implement PSK modulation and one uses the quadrature modulator shown in Figure \(\PageIndex{4}\). The discrete baseband signal \(\phi(t)\) could be internal to a DSP which is then interpolated in time and output by the DSP’s DAC as two smooth signals \(i(t) = \cos(\phi(t))\) and \(q(t) = \sin(\phi(t))\). On a phasor diagram \(i(t)\) and \(q(t)\) at the clock ticks addresses one of QPSK’s four states of the carrier’s phasor, see Figure \(\PageIndex{3}\).
For PSK modulation the constellation diagram is very similar to a phasor diagram that is continuously being re-normalized to the average power of
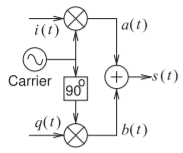
Figure \(\PageIndex{4}\): Quadrature modulator block diagram. In PSK modulation \(i(t)\) and \(q(t)\) have the same amplitude and indicate a phase \(\phi\) of the modulated carrier so that \(i(t) = \cos[\phi(t)]\) and \(q(t) = \sin[\phi(t)]\). The particular example shows two possible values of \(I_{k}\) and \(Q_{k}\) and this indicates QPSK modulation.
the modulated signal. This a subtle but important distinction, for example, a PSK baseband signal has a constellation diagram even though the baseband signal does not have a phasor representation. PSK modulation using the block diagram shown in Figure \(\PageIndex{4}\) has a carrier that is directly input to the top multiplier and a \(90^{\circ}\) phase-shifted version input to the bottom multiplier. Let the carrier be \(\cos(\omega_{c}t)\) and so the version of the carrier input to the bottom multiplier is \(\cos(\omega_{c}t − π/2) = −\sin(\omega_{c}t)\). So, with \(q(t)\) being a \(90^{\circ}\) phase-shifted version of \(i(t)\), (using the identities in Section 1.A.2 of [4]).
\[\begin{align}\label{eq:1}a(t)&=\cos(\phi(t))\cos(\omega_{c}t)=\frac{1}{2}\left[\cos(\omega_{c}t-\phi(t))+\cos(\omega_{c}t+\phi(t))\right] \\ \label{eq:2}b(t)&=\sin(\phi(t))\left[-\sin(\omega_{c}t)\right]=-\frac{1}{2}\left[\cos(\omega_{c}-\phi(t))-\cos(\omega_{c}t+\phi(t))\right] \\ \label{eq:3}s(t)&=a(t)+b(t)=\cos(\omega_{c}t+\phi(t))\end{align} \]
Thus \(s(t)\) is the single-sideband modulated carrier carrying information in the phase of the modulated carrier. The modulating signal \(\phi(t)\) is driven by a digital code that is designed so that \(\phi(t)\) changes at a minimum rate (it never has the same value for more than a few clock ticks). Thus there are no low frequency components of \(\phi(t)\) and thus there is no modulated signal at or very close to the carrier. Thus the carrier is suppressed but there is a sideband above and below the carrier frequency. This is SSB-SC modulation.
2.8.2 Binary Phase Shift Keying
PSK uses prescribed phase shifts to define symbols, each of which can represent one, two, or more bits. Binary Phase Shift Keying (BPSK), illustrated in Figures \(\PageIndex{1}\) and \(\PageIndex{2}\), has two phase states and conveys one bit per symbol and is a relatively spectrally inefficient scheme, with a maximum (i.e. ideal) modulation efficiency of \(1\text{ bits/s/Hz}\). The reason why the practical modulation efficiency is less than this number is because the transition from one phase state to the other must be constrained to avoid the modulated signal becoming very small, and also because there are no ideal lowpass filters to filter the input binary data stream. Although it has low modulation efficiency, it is ideally suited to low-power applications. BPSK is commonly used in Bluetooth.
The operation of BPSK modulation can be described using the constellation diagram shown in Figure \(\PageIndex{5}\)(a). The BPSK constellation diagram indicates that there are two states. These states can be interpreted as the rms values of \(i(t)\) and \(q(t)\) at the sampling times corresponding to the bit rate. The distance of a constellation point from the origin corresponds to (normalized) rms power of the pseudo-sinusoid of the modulated carrier at the sampling instant. (Normalization is with respect to the average power.) The curves in Figure \(\PageIndex{5}\)(b) indicate three transitions. The states are at the ends of the transitions. If a \(1\), in Figure \(\PageIndex{5}\)(b), is assigned to the positive \(I\) value and \(0\)
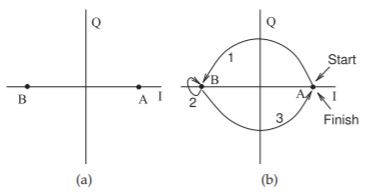
Figure \(\PageIndex{5}\): BPSK modulation with constellation points A and B: (a) constellation diagram; and (b) constellation diagram with possible transitions from one phase state to the other, or possibly no change in the phase state. In practical systems the transition should not go through the origin, as then the RF signal would drop below the noise level.

Figure \(\PageIndex{6}\): BPSK modulation: (a) constellation diagram; (b) constellation diagram with a constant amplitude transition; (c) time-domain waveform if the transition is fast; (d) time-domain waveform if the transition is slow; (e) constellation diagram with transition through the origin; and (f) time-domain waveform if the transition goes through the origin and is slow.
to a negative \(I\) value, then the bit sequence represented in Figure \(\PageIndex{5}\)(b) is “\(1001\).”
Figure \(\PageIndex{6}\)(a) is the constellation diagram of BPSK, with two symbols denoted as \(0\) and \(1\), and the trajectory of the transition from one constellation point to the other depending on the hardware used to implement the BPSK modulator. Figure \(\PageIndex{6}\)(b) shows the transition from the ‘\(0\)’ state to the ‘\(1\)’ state (and back) while maintaining a constant amplitude. If this transition is very fast, then the waveform produced is as shown in Figure \(\PageIndex{6}\)(c), where there are abrupt phase transitions and these have high spectral content. It is better to slow down the transitions, as then the waveform (shown in Figure \(\PageIndex{6}\)(d)), has smooth transitions and the bandwidth of the modulated carrier is minimal. The preferred smooth transition is obtained by lowpass filtering the baseband signal. That is, the abrupt transitions in the modulated RF signal result in the modulated signal having a broad bandwidth. The graceful transition of BPSK modulation limits the bandwidth of the modulated carrier.
A simple implementation of BPSK modulation would result in direct transition from one state to the others causing the phasor to traverse the origin and the amplitude of the RF signal to become very small and less than the noise level (see Figure \(\PageIndex{6}\)(e)). The resulting modulated RF waveform is
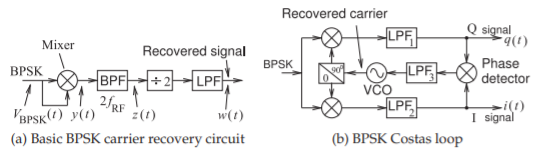
Figure \(\PageIndex{7}\): Block diagram of carrier recovery circuits for BPSK signals.
shown in Figure \(\PageIndex{6}\)(f). This is a problem because the receiver would not be able to track the RF signal.
Carrier Recovery
In a PSK demodulator, a local copy of the carrier must be produced to act as a reference in determining the phase of the modulated signal. The technique that produces the local copy of the unmodulated carrier is called carrier recovery. The circuit that directly implements carrier recovery of a BPSK signal is shown in Figure \(\PageIndex{7}\)(a). At the clock ticks the waveform of a BPSK modulated signal is
\[\label{eq:4}v_{\text{BPSK}}(t)=A(t)\cos(\omega_{\text{RF}}t+n\pi ) \]
where the carrier frequency \(f_{\text{RF}} = \omega_{\text{RF}}/(2π)\) and \(n\) can have a value of \(0\) or \(1\). Squaring this produces a signal
\[\begin{align}y(t)=v_{\text{BPSK}}^{2}(t)&=A^{2}(t)\cos^{2}(\omega_{\text{RF}}t+n\pi)=\frac{1}{2}A^{2}(t)[1+\cos(2\omega_{\text{RF}}t+n2\pi )]\nonumber \\ \label{eq:5}&=\frac{1}{2}A^{2}(t)[1+\cos(2\omega_{\text{RF}}t)]\end{align} \]
This is a signal at twice the carrier frequency with no carrier modulation since \(n2π\) and \(0\) radians are indistinguishable. The squaring operation is performed by mixing \(v_{\text{BPSK}}(t)\) with itself. Bandpass filtering \(y(t)\) produces a signal \(z(t)\) at the second harmonic of the carrier. The divide-by-2 block is implemented using a phase-locked loop (PLL). The result is the recovered carrier, \(w(t)\), that is used as the timing reference for sampling the demodulated I and Q components at precise times.
A better carrier recovery circuit than that in Figure \(\PageIndex{7}\)(a) and described above is the Costas loop [14] shown in Figure \(\PageIndex{7}\)(b). The BPSK Costas loop implements carrier recovery and I/Q demodulation simultaneously. In Figure \(\PageIndex{7}\)(b) \(i(t)\) and \(q(t)\) are mixed to produce a signal applied at the input of the third lowpass filter, \(\text{LPF}_{3}\). The main function of this filter is to remove noise and to average the signal coming out of the phase detector. The output of \(\text{LPF}_{3}\) drives a VCO in which the oscillation frequency is controlled by the applied voltage. The quadrature phase shifter then mixes the recovered carrier and a \(90^{\circ}\) shifted version with the BPSK signal.
It is critical that the signal-to-noise ratio (SNR), the ratio of the signal power to the noise power, of the BPSK signal be sufficiently large at all times or else the Costas loop will produce a noisy recovered carrier signal. If the modulated carrier becomes very small, for example when the trajectory on the constellation diagram goes through the origin (where the level of the carrier carrier falls below the noise level), the carrier will not be accurately recovered.
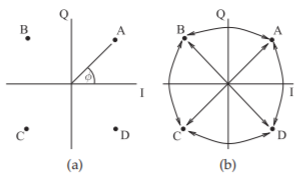
Figure \(\PageIndex{8}\): QPSK modulation: (a) constellation diagram; and (b) constellation diagram with possible transitions. Each constellation point indicates the phase, \(\phi\), of the modulated carrier, i.e. \(\cos(\omega_{c}t + \phi)\) where \(\omega_{c}\) is the radian frequency of the carrier.
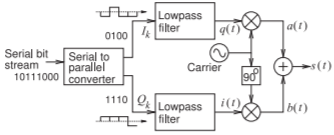
Figure \(\PageIndex{9}\): QPSK modulator block diagram. \(I_{k}\) and \(Q_{k}\) are similar to a stream of one-bit binary signals but are analog with a either a postitive value or a negative voltage so that after lowpass filtering \(i(t)\) and \(q(t)\) each have either a positive or a negative voltage at each clock tick.
2.8.3 Quadra-Phase Shift Keying, QPSK
In QPSK wireless systems, modulation efficiency is obtained by sending more than one bit of information per hertz of bandwidth (i.e., more than one bit per symbol). In QPSK information is encoded in four phase states and two bits are required to identify a symbol (i.e., to identify a phase state). The constellation diagram of QPSK is shown in Figure \(\PageIndex{8}\)(a) where the modulated RF carrier has four phase states identified as A, B, C, and D. So a QPSK modulator shifts the phase of the carrier to one of these phase states, and a QPSK demodulator must determine the phase of the received RF signal. The received RF signal is sampled with precise timing as determined by the recovered carrier signal. Thus two bits of information are transmitted per change of phase states. Each change of phase state requires at least \(1\text{ Hz}\) of bandwidth with the minimum bandwidth obtained when the transition from one state to another is no faster than that required to reach the new phase state before the sampling instant. QPSK modulation is also referred to as quarternary PSK.
QPSK can be implemented using the modulator shown in Figure \(\PageIndex{9}\). In Figure \(\PageIndex{9}\), the input bitstream is first converted into two parallel bitstreams each containing half the number of bits of the original bit stream. Thus a two-bit sequence in the serial bitstream becomes one \(I_{K}\) bit and one \(Q_{K}\) bit. The \((I_{K}, Q_{K})\) pair constitutes the \(K\)th symbol. The bitstreams are converted into waveforms \(i(t)\) and \(q(t)\) by the wave-shaping circuit.
The constellation diagram of QPSK is the result of plotting \(I\) and \(Q\) on a rectangular graph as shown in Figure \(\PageIndex{8}\)(a). All possible phase transitions are shown in Figure \(\PageIndex{8}\)(b). In the absence of wave-shaping circuits, \(i(t)\) and \(q(t)\) have very sharp transitions, and the paths shown in Figure \(\PageIndex{5}\)(b) occur almost instantaneously. This leads to large spectral spreads in the modulated waveform, \(s(t)\). So to limit the spectrum of the RF signal \(s(t)\), the shape of \(i(t)\) and \(q(t)\) is controlled; the waveform is shaped, usually by lowpass filtering. So a pulse-shaping circuit changes baseband binary information into a more smoothly varying signal. Each transition or path in Figure \(\PageIndex{5}\) represents the transfer of a symbol, with the best efficiency that can be obtained in wireless communication being one symbol per hertz of bandwidth. Each symbol contains two bits so the maximum modulation efficiency of QPSK modulation is \(2\text{ bits/s/Hz}\) of bandwidth. What is actually achieved depends on the wave-shaping circuits and on the criteria used to establish the bandwidth of \(s(t)\).
Carrier Recovery
Carrier recovery of a QPSK signal is similar to that for a BPSK signal. At the clock ticks an RF QPSK modulated signal
\[\label{eq:6}v_{\text{QPSK}}(t)=A(t)\cos (\omega_{\text{RF}}t+n\pi /2);\quad n=0,1,2,3, \]
where the carrier frequency \(f_{\text{RF}} = \omega_{\text{RF}}/(2π)\). The fourth power of this produces
\[\begin{align}v_{\text{QPSK}}^{4}(t)&=A^{4}(t)\cos^{4}(\omega_{\text{RF}}t+n\pi /2)\nonumber \\ \label{eq:7}&=\frac{1}{8}A^{4}(t)[3+4\cos (2\omega_{\text{RF}}t+n\pi)+\cos(4\omega_{\text{RF}}t+n2\pi)]\end{align} \]
Following bandpass filtering at \(4f_{\text{RF}}\) and then dividing the frequency by \(4\), the carrier is recovered. Circuits implementing this are similar to those for recovering the carrier of BPSK signals. This concept can be extended to carrier recovery for any \(M\)-PSK-modulated signal.
Example \(\PageIndex{1}\): QPSK Modulation and Constellation
The bit sequence \(\mathsf{110101001100}\) is to be transmitted using QPSK modulation. Show the transitions on a constellation diagram.
Solution
The bit sequence \(\mathsf{110101001100}\) must be converted to a two-bit-wide parallel stream of symbols resulting in the sequence of symbols \(\mathsf{11 01 01 00 11 00}\). The symbol \(\mathsf{11}\) transitions to the symbol \(\mathsf{01}\) and then to the symbol \(\mathsf{01}\) and so on. The states (or symbols) and the transitions from one symbol to the next required to send the bitstream \(\mathsf{110101001100}\) are shown in Figure \(\PageIndex{10}\). QPSK modulation results in the phasor of the carrier transitioning through the origin so that the average power is lower and the PMEPR is high. A more significant problem is that the phasor will fall below the noise floor, making carrier recovery almost impossible.
2.8.4 \(\pi /4\) Quadrature Phase Shift Keying
A major objective in digital modulation is to ensure that the RF trajectory from one phase state to another does not go through the origin. The transition is slow, so that if the trajectory goes through the origin, the amplitude of the carrier will be below the noise floor for a considerable time and it will not be possible to recover the carrier reference. This is why the QPSK scheme is not used directly in 2G and 3G cellular radio. (The 4G and 5G cellular radio systems do use QPSK among other modulation schemes and use pilot tones to recover the carrier.) One of the solutions developed to address this problem is the \(π/4\) quadrature phase shift keying (\(π/4\)-QPSK) modulation scheme. In this scheme the constellation at each symbol is rotated \(π/4\) radians from the previous symbol, as shown in Figure \(\PageIndex{11}\). (In an alternative implementation of \(π/4\)-QPSK modulation the constellation diagram could

Figure \(\PageIndex{10}\): Constellation diagram and transitions for the bit sequence \(\mathsf{110101001100}\) sent as the set of symbols \(\mathsf{11 01 01 00 11 00}\) using QPSK. Note that symbols \(2\) and \(3\) are identical, so there is no transition. The \(\mathsf{SYMBOL}\) numbers indicated reference the symbol at the end of the transition (end of the arrow). The assignment of bits to symbols (e.g., assigning the bits ‘\(11\)’ to the symbol in the first quadrant) is arbitrary in general but the assignment of symbols is defined in a particular standard.
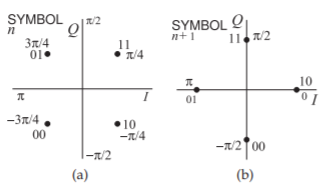
Figure \(\PageIndex{11}\): Constellation diagram of \(π/4\)- QPSK modulation: (a) initial constellation diagram at one symbol; and (b) the constellation diagram at the time of the next symbol.
rotate by \(π/4\) continuously rather than switching between conditions as described here.)
One of the unique characteristics of \(π/4\)-QPSK modulation is that there is always a change, even if a symbol is repeated. This helps with recovering the carrier frequency. If the binary bitstream itself (with sharp transitions in time) is the modulation signal, then the transition from one symbol to the next occurs instantaneously and hence the modulated signal has a broad spectrum around the carrier frequency. The transition, however, is slower if the bitstream is filtered, and so the bandwidth of the modulated signal will be less. Ideally the transmission of one symbol per hertz would be obtained. However, in \(π/4\)-QPSK modulation the change from one symbol to the next has a variable distance (and so a transition takes different times) so that the ideal modulation efficiency of one symbol per second per hertz (or \(2\)
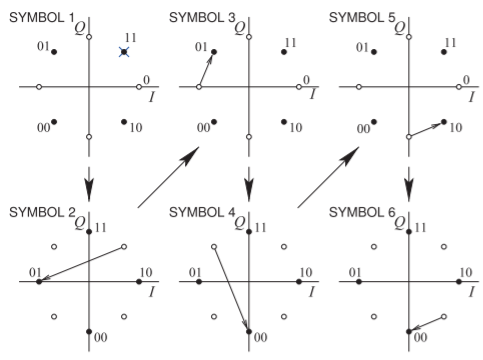
Figure \(\PageIndex{12}\): Constellation diagram states and transitions for the bit sequence \(\mathsf{110101001000}\) sent as the set of symbols \(\mathsf{11 01 01 00 10 00}\) using \(π/4\)QPSK modulation.
\(\text{bits/s/Hz}\)) is not obtained. In practice, with realistic filters and allowing for the longer transitions, \(π/4\)-QPSK modulation achieves \(1.62\text{ bits/s/Hz}\).
Example \(\PageIndex{2}\): \(\pi /4\)-QPSK Modulation and Constellation
The bit sequence \(\mathsf{110101001000}\) is transmitted using \(π/4\)-QPSK modulation. Show the transitions on a constellation diagram.
Solution
The bit sequence \(\mathsf{110101001000}\) must be converted to a two-bit-wide parallel stream of symbols, resulting in the sequence of symbols \(\mathsf{11 01 01 00 10 00}\). The symbol \(\mathsf{11}\) transitions to the symbol \(\mathsf{01}\) and then to the symbol \(\mathsf{01}\) and so on. The constellation diagram of \(π/4\)-QPSK modulation really consists of two QPSK constellation diagrams that are shifted by \(π/4\) radians, as shown in Figure \(\PageIndex{11}\). At one symbol (or time) the constellation diagram is that shown in Figure \(\PageIndex{11}\)(a) and at the next symbol it is that shown in Figure \(\PageIndex{11}\)(b). The next symbol uses the constellation diagram of Figure \(\PageIndex{11}\)(a) and the process repeats. The states (or symbols) and the transitions from one symbol to the next that are required to send the bitstream \(\mathsf{110101001000}\) are shown in Figure \(\PageIndex{12}\).
2.8.5 Differential Quadra Phase Shift Keying, DQPSK
Multiple transmission paths, or multipaths, due to reflections result in constructive and destructive interference and can result in rapid additional phase rotations. Thus relying on the phase of a phasor at the symbol sample time, at the clock ticks, to determine the symbol transmitted is prone to error. When an error results at one symbol, this error accumulates when subsequent symbols are extracted. The solution is to use encoding, and one of the simplest encoding schemes is differential phase encoding. In this scheme the information of the modulated signal is contained in changes in phase rather than in the absolute phase. That is, the transition defines the symbol rather than the end point of the transition.
The \(π/4\)-DQPSK modulation scheme is a differentially encoded form of
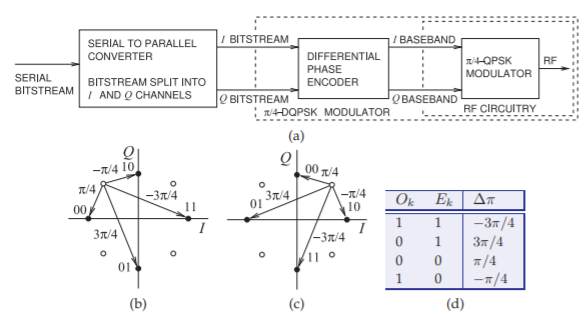
Figure \(\PageIndex{13}\): A \(π/4\)-DQPSK modulator: (a) differential phase encoder with a \(π/4\)-QPSK modulator; (b) constellation diagram of \(π/4\)-DQPSK; (c) a second constellation diagram; and (d) phase changes in a \(π/4\)-DQPSK modulation scheme. Note that the information is in the phase change rather than the phase state.
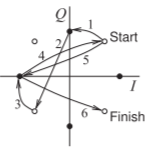
Figure \(\PageIndex{14}\): Constellation diagram of \(π/4\)- DQPSK modulation showing six symbol intervals coding the bit sequence \(\mathsf{000110110101}\).
\(π/4\)-QPSK. The \(π/4\)-DQPSK scheme incorporates the \(π/4\)-QPSK modulator and an encoding scheme, as shown in Figure \(\PageIndex{13}\)(a). The scheme is defined with respect to its constellation diagram, shown in Figure \(\PageIndex{14}\)(b) and repeated in Figure \(\PageIndex{13}\)(c) for clarity. The D indicates differential coding, while the \(π/4\) denotes the rotation of the constellation by \(π/4\) radians from one interval to the next. This can be explained by considering Figure \(\PageIndex{13}\)(a). A four-bit stream is divided into two quadrature nibbles of two bits each. These nibbles independently control the \(I\) and \(Q\) encoding, respectively, so that the allowable transitions rotate according to the last transition. The information or data is in the phase transitions rather than the constellation points themselves. The relationship between the symbol value and the transition is given in Figure \(\PageIndex{13}\)(d). For example, the transitions shown in Figure \(\PageIndex{14}\) for six successive time intervals describes the input bit sequence \(\mathsf{000110110101}\). Its waveform and spectrum are shown in Figure \(\PageIndex{15}\). More detail of the spectrum is shown in Figure \(\PageIndex{16}\). In practice with realistic filters and allowing for the longer transitions, \(π/4\)-DQPSK modulation achieves a modulation efficiency of \(1.62\text{ bits/s/Hz}\), the same as \(π/4\)-QPSK, but of course with greater resilience to changes in the transmission path.
In a differential scheme, the data transmitted are determined by
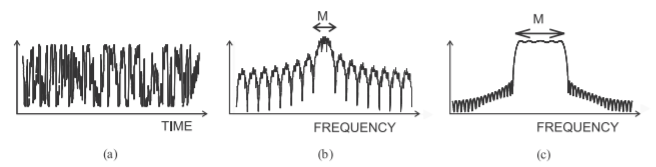
Figure \(\PageIndex{15}\): Details of digital modulation obtained using differential phase shift keying (\(π/4\)- DQPSK): (a) modulating waveform; (b) spectrum of the modulated carrier, with \(\mathsf{M}\) denoting the main channel; and (c) details of the spectrum of the modulated carrier focusing on the main channel.
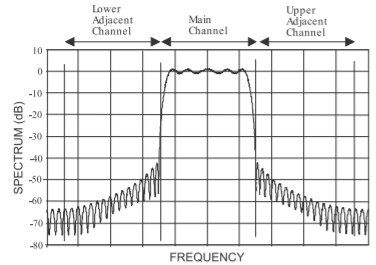
Figure \(\PageIndex{16}\): Detailed spectrum of a \(π/4\)-DQPSK signal showing the main channel and lower and upper adjacent channels.
comparing a symbol with the previously received symbol, so the data are determined from the change in phase of the carrier rather than the actual phase of the carrier. This process of inferring the data actually sent from the received symbols is called decoding. When \(π/4\)-DQPSK encoding was introduced in the early 1990s the DSP available for a mobile handset had only just reached sufficient complexity. Today, encoding is used with all digital radio systems and is more sophisticated than just the differential scheme of DQPSK. There are new ways to handle carrier phase ambiguity. The sophistication of modern coding schemes is beyond the scope of the hardware-centric theme of this book.
2.8.6 Offset Quadra Phase Shift Keying, OQPSK
The offset quadra phase shift keying (OQPSK) modulation scheme avoids transitions passing through the origin on the constellation diagram (see Figure \(\PageIndex{18}\)(a)). As in all QPSK schemes, there are two bits per symbol, but now one bit is used to immediately modulate the RF signal, whereas the other bit is delayed by half a symbol period, as shown in Figure \(\PageIndex{17}\). The maximum phase change for a bit transition is \(90^{\circ}\), and as \(Q_{K}\) is delayed, a total phase change of approximately \(180^{\circ}\) is possible during one symbol. The
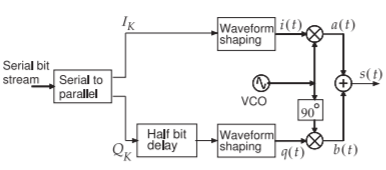
Figure \(\PageIndex{17}\): Block diagram of an OQPSK modulator.
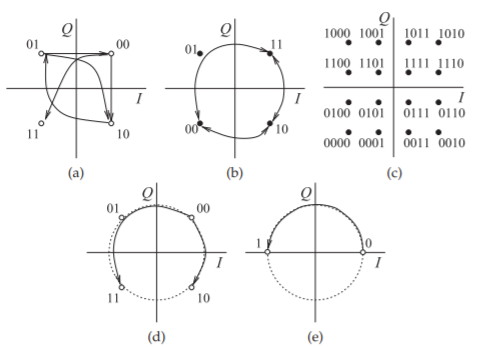
Figure \(\PageIndex{18}\): Constellation diagrams for various modulation formats: (a) OQPSK; (b) GMSK; (c) 16-QAM; (d) SOQPSK (also FOQPSK); and (e) SBPSK.
constellation diagram is shown in Figure \(\PageIndex{18}\)(a).
The OQPSK modulator can be implemented using relatively simple electronics with a digital delay circuit delaying the \(Q\) bit by half a symbol period and lowpass filters shaping the \(I\) and \(Q\) bits. The OQPSK scheme is also called staggered quadrature phase shift Keying (SQPSK). Better performance can be obtained by using DSP to shape the \(I\) and \(Q\) transitions so that they change smoothly and the phasor trajectory nearly follows a circle. Consequently \(I\) and \(Q\) change together, but in such a manner that the PMEPR is maintained close to \(0\text{ dB}\). Two modulation techniques that implement this are the shaped offset QPSK (SOQPSK) and the Feher QPSK (FQPSK) schemes. The constellation diagrams for SOQPSK and FQPSK are shown in Figure \(\PageIndex{18}\)(d). These are constant envelope digital modulation schemes. As with OQPSK, the \(Q\) bit is delayed by one-half of a symbol period and the \(I\) and \(Q\) baseband signals are shaped by a half-sine filter. The advantage is that high-efficiency saturating amplifier designs can be used and battery life extended. There is a similar modulation format called shaped binary phase shift keying (SBPSK) which, as expected, has two constellation points as shown in Figure \(\PageIndex{18}\)(e). SOQPSK, FQPSK, and SBPSK are continuous phase modulation (CPM) schemes, as the phase
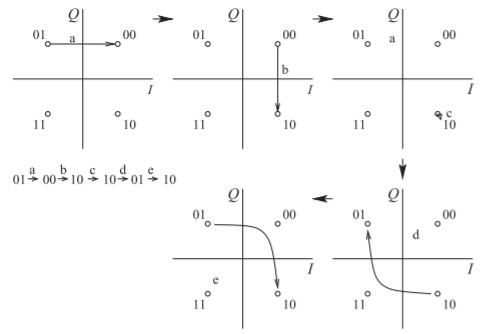
Figure \(\PageIndex{19}\): Constellation diagram of OQPSK modulation for the bit sequence \(\mathsf{010010100110}\).
never changes abruptly. Instead, the phase changes smoothly, achieving high modulation efficiency and maintaining a constant envelope. Implementation of the receiver, however, is complex. CPM schemes have good immunity to interference and are commonly used in military systems.
Example \(\PageIndex{3}\): OQPSK Modulation
Draw the constellation diagrams for the bit sequence \(\mathsf{010010100110}\) using OQPSK modulation.
Solution
The bit sequence is first separated into the parallel stream \(\mathsf{01-00-10-10-01-10}\). The \(I\) bit changes first, followed by the \(Q\) bit delayed by half of the time of a bit. Five constellation diagrams are shown in Figure \(\PageIndex{19}\) with the transitions sending the bit sequence.
2.8.7 \(3\pi /8\)-8PSK, Rotating Eight-State Phase Shift Keying
The \(3π/8\)-8PSK modulation scheme is similar to \(π/4\)-DQPSK in the sense that rotation of the constellation occurs from one time interval to the next. This time, however, the rotation of the constellation from one symbol to the next is \(3π/8\). This modulation scheme is used in the enhanced data rates for GSM evolution (EDGE) system, and provides three bits per symbol (ideally) compared to GMSK used in GSM which has two bits per symbol (ideally). With some other changes, GSM/EDGE provides data transmission of up to \(128\text{ kbits/s}\), faster than the \(48\text{ kbits/s}\) possible with GSM.
Quadrature modulation schemes with four states, such as QPSK, have two \(I\) states and two \(Q\) states that can be established by lowpass filtering the \(I\) and \(Q\) bitstreams. For higher-order modulation schemes such as 8-PSK, this approach will not work. Instead, \(i(t)\) and \(q(t)\) are established in the DSP unit and then converted using a DAC to generate the analog signals applied
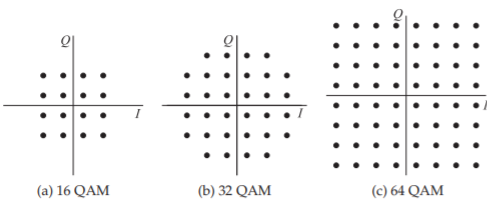
Figure \(\PageIndex{20}\): QAM constellation diagrams.
to the hardware modulator. Alternatively the modulated signal is created directly in the DSP and a DAC converts this to an IF and a hardware mixer up-converts this to RF. QAM
2.8.8 Summary
PSK modulation is implemented in many radio standards including all cellular standards after 2G. There was a 2G system that used \(π/4\)DQPSK but that is no longer supported. The modern radio standards support many modulation formats but in high interference situations BPSK, QPSK and 8-PSK have the best performance. While QPSK was dismissed in 2G and 3G because of difficulties with carrier recovery, 4G and 5G have another method for implementing carrier recovery which allows QPSK on its own to be used. GMSK is still supported by modern cellular phones but the infrastructure, i.e. basestations, are starting to be retired.
Most of the modulation schemes described in this section were introduced as optimum trade-offs of modulation efficiency, resistance to interference, and hardware complexity. Some, such as BPSK, draw very little power and are suited to the internet-of-things (IoT) applications which must have a battery lifetime of ten years.
Footnotes
[1] This theorem was discovered independently by several people and is also known as the Nyquist-Shannon sampling theorem, the Nyquist-Shannon-Kotelnikov, the Whittaker-Shannon-Kotelnikov, the Whittaker-Nyquist-Kotelnikov-Shannon (WKS), as well as the cardinal theorem of interpolation theory. The theorem states [13]: “If a function \(x(t)\) contains no frequencies higher than \(B\) hertz, it is completely determined by giving its ordinates at a series of points spaced \(1/(2B)\) seconds apart.”


