3.2: Distributed Amplifiers

Distributed amplifiers use the ability of transmission lines to combine the output of multiple transistor stages to realize an amplifier with a bandwidth of more than a decade [1, 2]. While the bandwidth is wider than that of the single-stage wideband amplifier discussed in the previous section, the efficiency is much lower.

The topology of a four-stage distributed amplifier is shown in Figure \(\PageIndex{1}\)(a). The distributed amplifier has two transmission lines, referred to as the gate line and drain line. Each stage includes an active device and two sections of transmission line, one being part of the gate line and the other being part of the drain line. The small-signal model of the input is shown in Figure \(\PageIndex{1}\)(b) and that of the output in Figure \(\PageIndex{1}\)(c). In the small signal model, the input of the transistor is modeled as a series resistance, \(R_{i,n}\), and capacitance, \(C_{gs,n}\), and these load the gate line. Ignoring \(R_{i,n}\) for now, the small-signal input model is a transmission line that is loaded periodically by capacitors. This therefore appears as an artificial transmission line. If the line is terminated in an appropriate resistance, \(R_{1}\), then no input signal is reflected at the end of the line segment. Proper design would result in very little power on the gate line after the final stage, as power is periodically coupled into the transistors. Design also ensures that there is a negligible backward-traveling wave on the input transmission line.

The small-signal model of the output drain line is similar, with a line periodically loaded by the output resistance and capacitance of the transistors. Now, however, there is a controlled current source that injects power onto the drain line. If there was only one stage, then the power delivered to the drain line would be split equally between forward- and backward-traveling components. However, here there are multiple stages, and the phase of the drain current injection changes along the line and current is preferably coupled into the forward-traveling wave. Still a termination resistor \(R_{2}\) ensures that there is no backward-traveling wave on the drain line.

Power is periodically being tapped off of the gate line and an amplified signal is periodically inserted on the drain line. As a result, the transistors

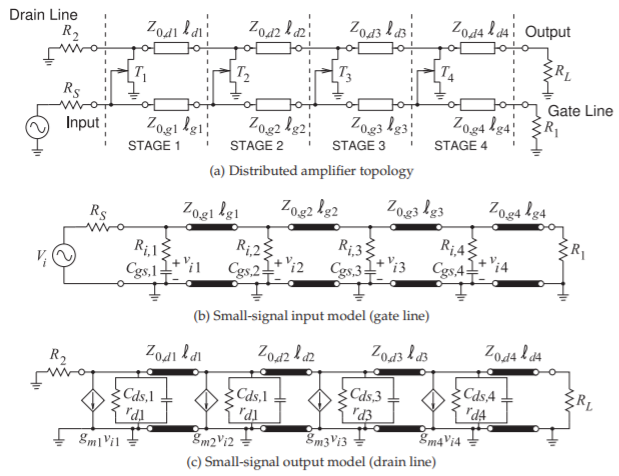
Figure \(\PageIndex{1}\): Distributed amplifier with four stages.

often are designed to increase in size along the length of the line. In this case the input and output capacitances of the transistors increase with each stage. Even if the transistors in each stage are of equal size, the characteristic impedances of the drain and gate transmission lines vary for each stage, and the lengths of the lines in the drain stage are not the same as the lengths of the lines in the gate line.

Distributed amplifiers can simplify stability constraints and enable amplification over multiple octaves. They also find application at millimeter-wave frequencies even when bandwidths of greater than one-half octave are not required [3]. At millimeter-wave frequencies parasitic capacitances are significant and these can be incorporated into the synthesis of the loaded transmission lines. Since the need to cancel parasitic capacitances is not required, it can be easier to achieve stable amplification.