3.4: Frequency Response
- Page ID
- 60843
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The frequency response of an element or system is a measure of its steady-state performance under conditions of sinusoidal excitation. In steady state, the output of a linear element excited with a sinusoid at a frequency \(\omega\) (expressed in radians per second) is purely sinusoidal at frequency \(\omega\). The frequency response is expressed as a gain or magnitude \(M(\omega)\) that is the ratio of the amplitude of the output to the input sinusoid and a phase angle \(\phi (\omega)\) that is the relative angle between the output and input sinusoids. The phase angle is positive if the output leads the input. The two components that comprise the frequency response of a system with a transfer function \(G(s)\) are given by
\[M(\omega) = |G(j\omega)| \nonumber \]
\[\phi (\omega) = \measuredangle G(j \omega) = \tan^{-1} \dfrac{\text{Im} [G(j\omega)]}{\text{Re} [G(j\omega)]} \nonumber \]
It is frequently necessary to determine the frequency response of a system with a transfer function that is a ratio of polynomials in \(s\). One possible method is to evaluate the frequency response by substituting \(j\omega\) for \(s\) at all frequencies of interest, but this method is cumbersome, particularly for high-order polynomials. An alternative approach is to present the in formation concerning the frequency response graphically, as described below.
The transfer function is first factored so that both the numerator and denominator consist of products of first- and second-order terms with real coefficients. The function can then be written in the general form
\[\begin{array} {rcl} {G(s)} & = & {\dfrac{a_0}{s^n} \left [\prod_{\text{first-order zeros}} (\tau_h s + 1)\right ] \left [\prod_{\text{complex zero pairs}} \left (\dfrac{s^2}{\omega_{ni}^2} + \dfrac{2\zeta_i s}{\omega_{ni}} + 1 \right )\right ]} \\ {} & \ & {\times \left [\prod_{\text{first-order poles}} \dfrac{1}{(\tau_j s + 1)}\right ] \left [\prod_{\text{complex pole pairs}} \dfrac{1}{(s^2/\omega_{nk}^2 + 2 \zeta_k s/\omega_{nk} + 1)}\right ]} \end{array}\label{eq3.4.3} \]
While several methods such as Lin's method(S. N. Lin, "A Method of Successive Approximations of Evaluating the Real and Com plex Roots of Cubic and Higher-Order Equations," J. Math. Phys., Vol. 20, No. 3, August, 1941, pp. 231-242.) are available for factoring polynomials, this operation can be tedious unless machine computation is employed, particularly when the order of the polynomial is large. Fortunately, in many cases of interest the polynomials are either of low order or are available from the system equations in factored form.
Since \(G(j \omega)\) is a function of a complex variable, its angle \(\phi (\omega)\) is the sum of the angles of the constituent terms. Similarly, its magnitude \(M(\omega)\) is the product of the magnitudes of the components. Furthermore, if the magnitudes of the components are plotted on a logarithmic scale, the log of \(M\) is given by the sum of the logs corresponding to the individual components.(The decibel, equal to 20 logio [magnitude] is often used for these manipulations. This usage is technically correct only if voltage gains or current gains between portions of a circuit with identical impedance levels are considered. The issue is further confused when the decibel is used indiscriminately to express dimensioned quantities such as transconductances. We shall normally reserve this type of presentation for loop-transmission manipulations (the loop transmission of any feedback system must be dimensionless), and simply plot signal ratios on logarithmic coordinates.)
Plotting is simplified by recognizing that only four types of terms are possible in the representation of Equation \(\ref{eq3.4.3}\):
- Constants, \(a_0\).
- Single- or multiple-order differentiations or integrations, \(s^n\), where \(n\) can be positive (differentiations) or negative (integrations).
- First-order terms \((\tau s + 1)\), or its reciprocal.
- Complex conjugate pairs \(s^2 / \omega_n^2 + 2 \zeta s /\omega_n + 1\), or its reciprocal.
It is particularly convenient to represent each of these possible terms as a plot of \(M\) (on a logarithmic magnitude scale) and \(\phi\) (expressed in degrees) as a function of o (expressed in radians per second) plotted on a logarithmic frequency axis. A logarithmic frequency axis is used because it provides adequate resolution in cases where the frequency range of interest is wide and because the relative shape of a particular response curve on the log axis does not change as it is frequency scaled. The magnitude and angle of any rational function can then be determined by adding the magnitudes and angles of its components. This representation of the frequency response of a system or element is called a Bode plot.
The magnitude of a term ao is simply a frequency-independent constant, with an angle equal to \(0^{\circ}\) or \(180^{\circ}\) depending on whether the sign of ao is positive or negative, respectively.
Both differentiations and integrations are possible in feedback systems. For example, a first-order high-pass filter has a single zero at the origin and, thus, its voltage transfer ratio includes a factor \(s\). A motor (frequently used in mechanical feedback systems) includes a factor \(1/s\) in the transfer function that relates mechanical shaft angle to applied motor voltage, since a constant input voltage causes unlimited shaft rotation. Similarly, various types of phase detectors are examples of purely electronic elements that have a pole at the origin in their transfer functions. This pole results be cause the voltage out of such a circuit is proportional to the phase-angle difference between two input signals, and this angle is equal to the integral of the frequency difference between the two signals. We shall also see that it is often convenient to approximate the transfer function of an amplifier with high d-c gain and a single low-frequency pole as an integration.
The magnitude of a term \(s^n\) is equal to \(\omega^n\), a function that passes through 1 at \(\omega = 1\) and has a slope of \(n\) on logarithmic coordinates. The angle of this function is \(n \times 90^{\circ}\) at all frequencies.
The magnitude of a first order pole \(1/(\tau s + 1)\) is
\[M = \dfrac{1}{\sqrt{\tau^2 \omega^2 + 1}} \nonumber \]
while the angle of this function is
\[\phi = -\tan^{-1} \tau \omega \nonumber \]
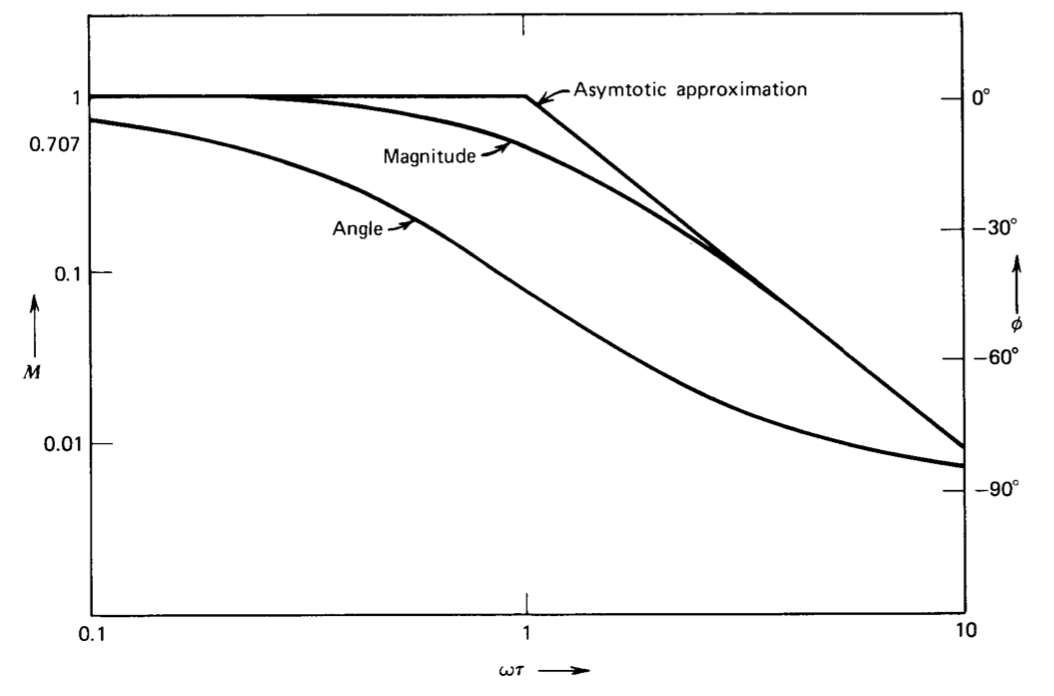
The magnitude and angle for the first-order pole are plotted as a function of normalized frequency in Figure 3.11. An essential feature of the magnitude function is that it can be approximated by two straight lines, one lying along the \(M = 1\) line and the other with a slope of -1, which intersect at \(\omega = 1/\tau\). (This frequency is called the corner frequency.) The maximum departure of the actual curves from the asymptotic representation is a factor of 0.707 and occurs at the corner frequency. The magnitude and angle for a first-order zero are obtained by inverting the curves shown for the pole, so that the magnitude approaches an asymptotic slope of +1 beyond the corner frequency, while the angle changes from 0 to +\(90^{\circ}\).
The magnitude for a complex-conjugate pole pair
\[\dfrac{1}{s^2 / \omega_n^2 + 2 \zeta s/ \omega_n + 1}\nonumber \]
is
\[M = \dfrac{1}{\sqrt{\dfrac{4\zeta^2 \omega^2}{\omega_n^2} + \left (1 - \dfrac{\omega^2}{\omega_n^2} \right )^2}} \nonumber \]
with the corresponding angle
\[\phi = -\tan^{-1} \dfrac{2 \zeta \omega /\omega_n}{1 - \omega^2 /\omega_n^2} \nonumber \]
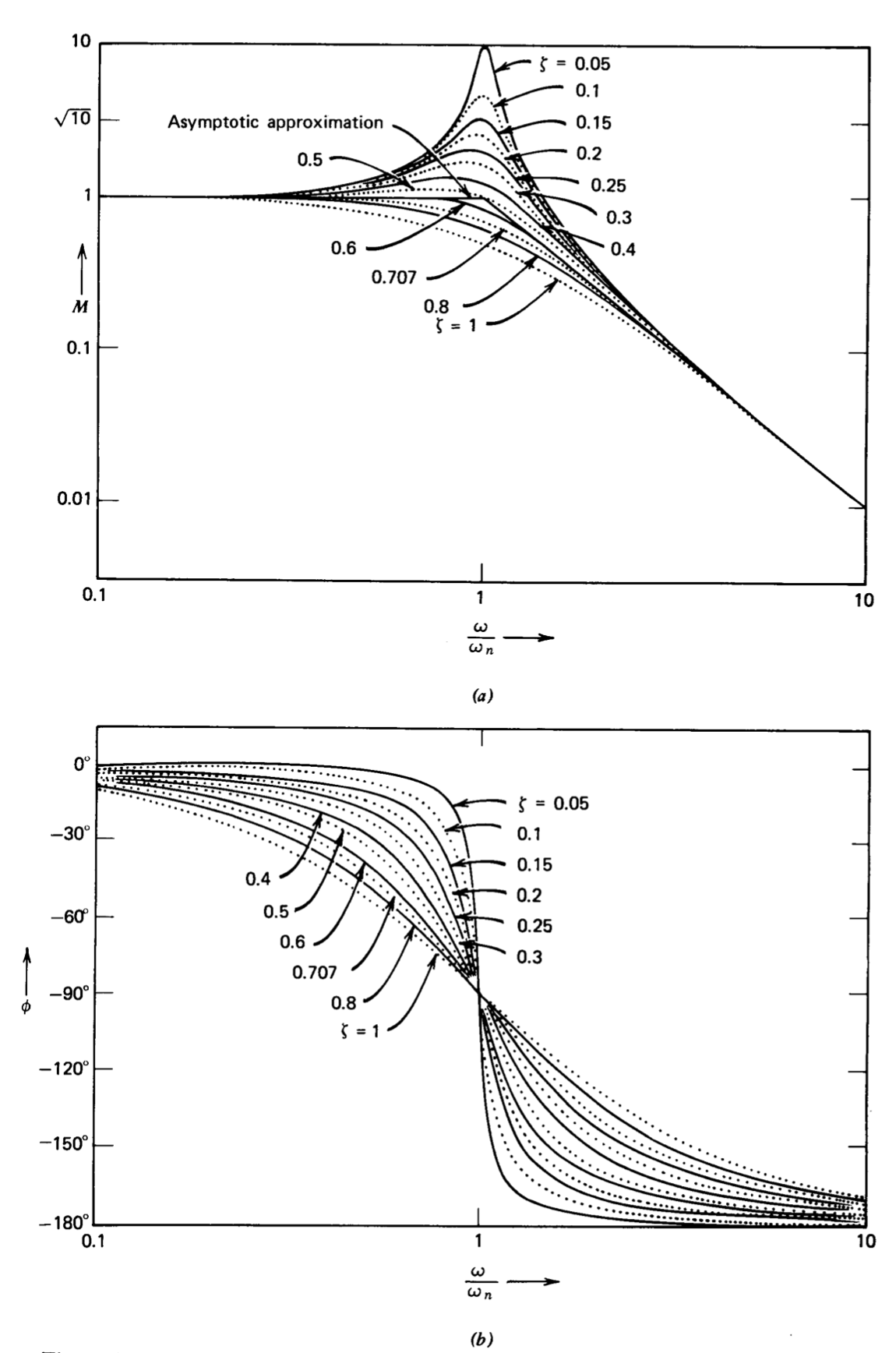
These functions are shown in Bode-plot form as a parametric family of curves plotted against normalized frequency \(\omega / \omega_n\) in Figure 3.12. Note that the asymptotic approximation to the magnitude is reasonably accurate providing that the damping ratio exceeds 0.25. The corresponding curves for a complex-conjugate zero are obtained by inverting the curves shown in Figure 3.12.
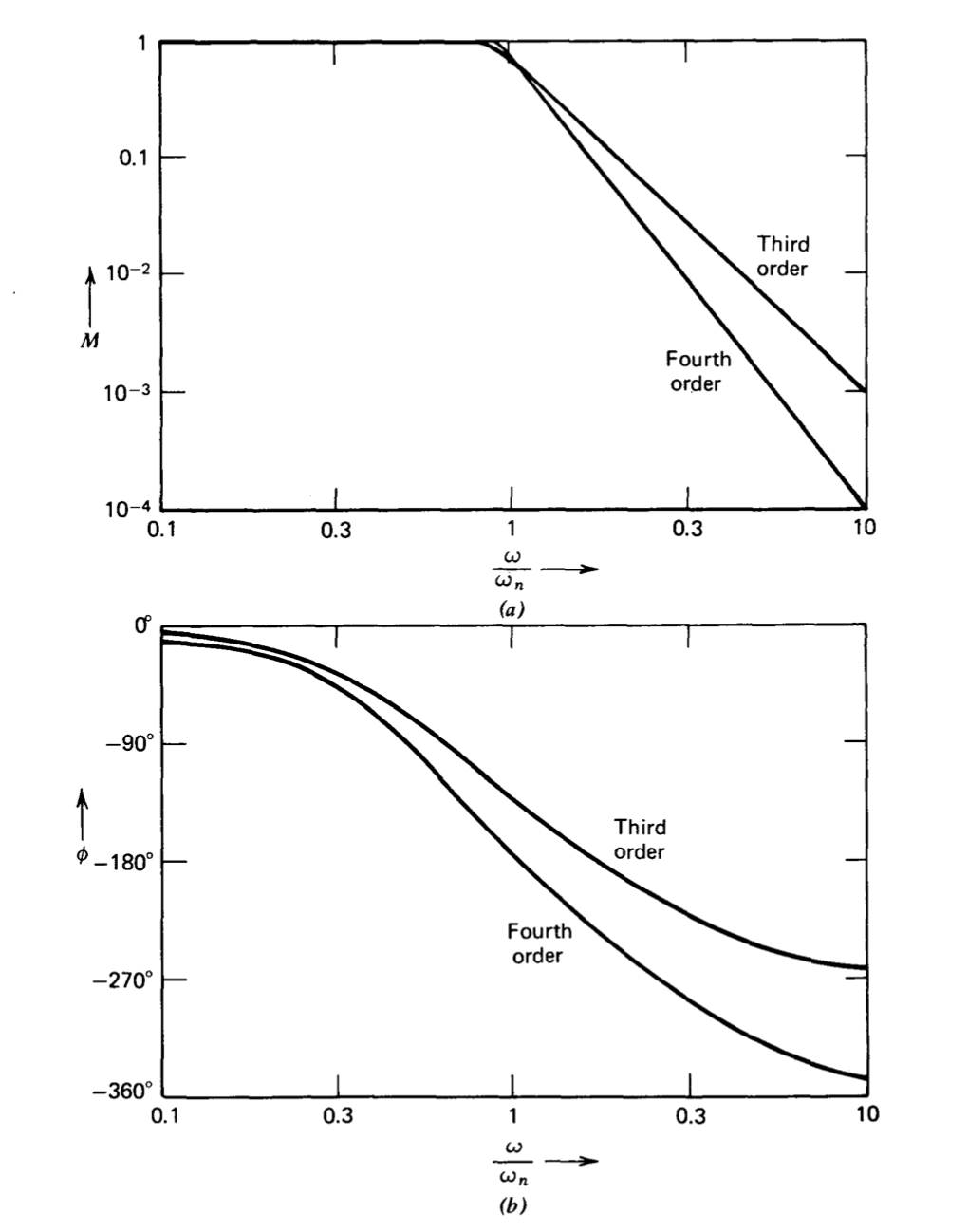
It was stated in Section 3.3.2 that feedback amplifiers are occasionally adjusted to have Butterworth responses. The frequency responses for third- and fourth-order Butterworth filters are shown in Bode-plot form in Figure 3.13. Note that there is no peaking in the frequency response of these
maximally-flat transfer functions. We also see from Figure 3.12 that the damping ratio of 0.707, corresponding to the two-pole Butterworth configuration, divides the second-order responses that peak from those which do not. The reader should recall that the flatness of the Butterworth response refers to its frequency response, and that the step responses of all Butterworth filters exhibit overshoot.
The value associated with Bode plots stems in large part from the ease with which the plot for a complex system can be obtained. The overall system transfer function can be obtained by the following procedure. First, the magnitude and phase curves corresponding to all the terms included in the transfer function of interest are plotted. When the first- and second-order curves (Figs. 3.11 and 3.12) are used, they are located along the frequency axis so that their corner frequencies correspond to those of the represented factors. Once these curves have been plotted, the magnitude of the complete transfer function at any frequency is obtained by adding the linear distances from unity magnitude of all components at the frequency of interest. The same type of graphical addition can be used to obtain the complete phase curve. Dividers, or similar aids, can be used to per form the graphical addition.
In practice, the asymptotic magnitude curve is usually sketched by drawing a series of intersecting straight lines with appropriate slope changes at intersections. Corrections to the asymptotic curve can be added in the vicinity of singularities if necessary.
The information contained in a Bode plot can also be presented as a gain-phase plot, which is a more convenient representation for some operations. Rectangular coordinates are used, with the ordinate representing the magnitude (on a logarithmic scale) and the abscissa representing the phase angle in degrees. Frequency expressed in radians per second is a parameter along the gain-phase curve. Gain-phase plots are frequently drawn by transferring data from a Bode plot.
The transfer function
\[G(s) = \dfrac{10^7(10^{-4} + 1)}{s(0.01s + 1) (s^2/10^{12} + 2 (0.2) s/ 10^6 + 1)} \nonumber \]
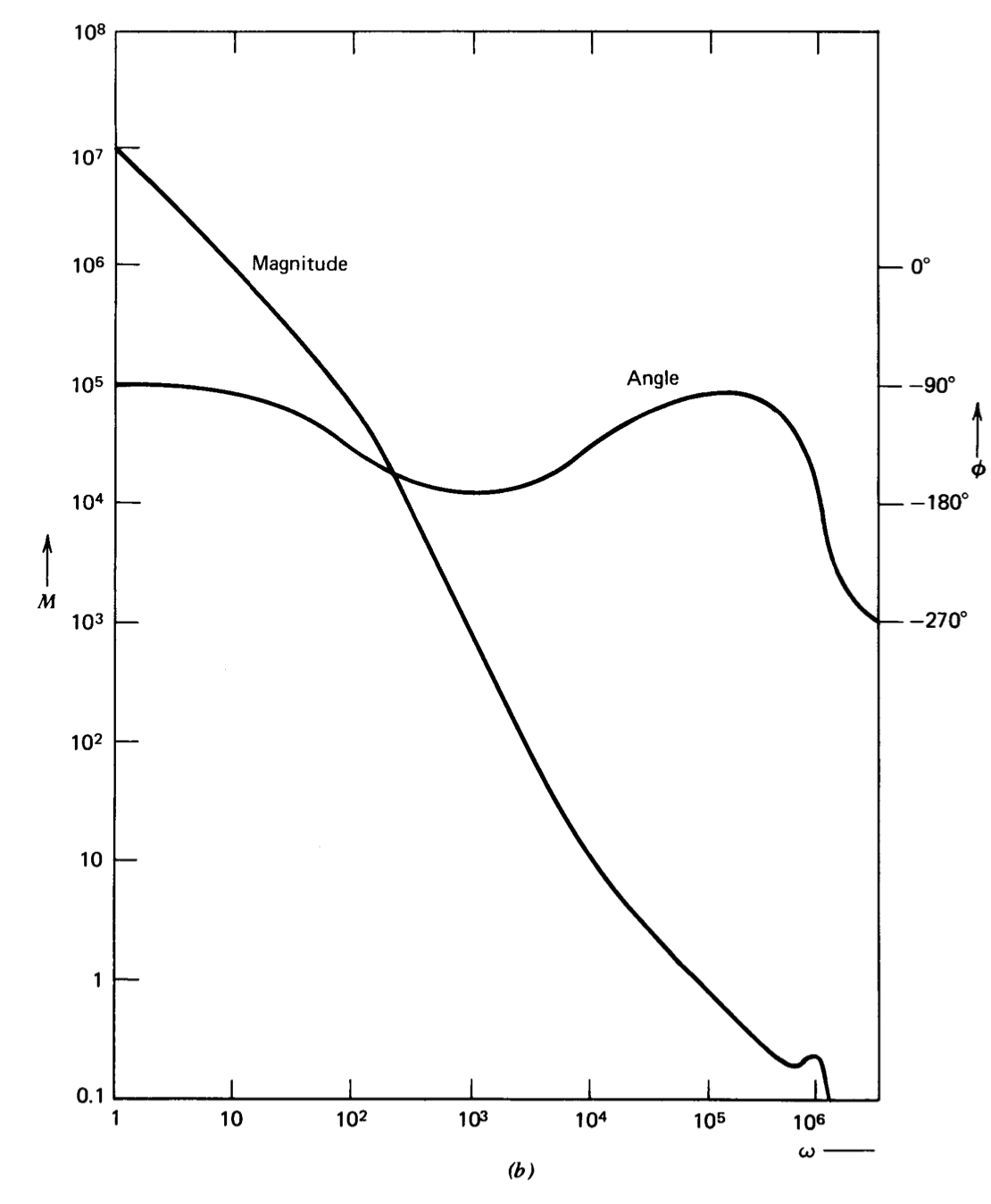
is used to illustrate construction of Bode and gain-phase plots. This function includes these five factors:
- A constant \(10^7\).
- A single integration.
- A first-order pole with a time constant of 0.01 second, corresponding to a corner frequency of 100 radians per second.
- A first-order zero with a time constant of \(10^{-4}\) seconds, corresponding to a corner frequency of \(10^4\) radians per second.
- A complex-conjugate pole pair with a natural frequency of \(10^6\) radians per second and a damping ratio of 0.2.
The individual factors are shown in Bode-plot form on a common frequency scale in Figure 3.14\(a\). These factors are combined to yield the Bode plot for the complete transfer function in Figure 3.14\(b\). The same information is presented in gain-phase form in Figure 3.15.


