3.6: ERROR COEFFICIENTS
- Page ID
- 60845
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The response of a linear system to certain types of transient inputs may be difficult or impossible to determine by Laplace techniques, either be cause the transform of the transient is cumbersome to evaluate or because the transient violates the conditions necessary for its transform to exist. For example, consider the angle that a radar antenna makes with a fixed reference while tracking an aircraft, as shown in Figure 3.18. The pointing angle determined from the geometry is
\[\theta = \tan^{-1} \left [\dfrac{v}{l} t \right ]\label{eq3.6.1} \]
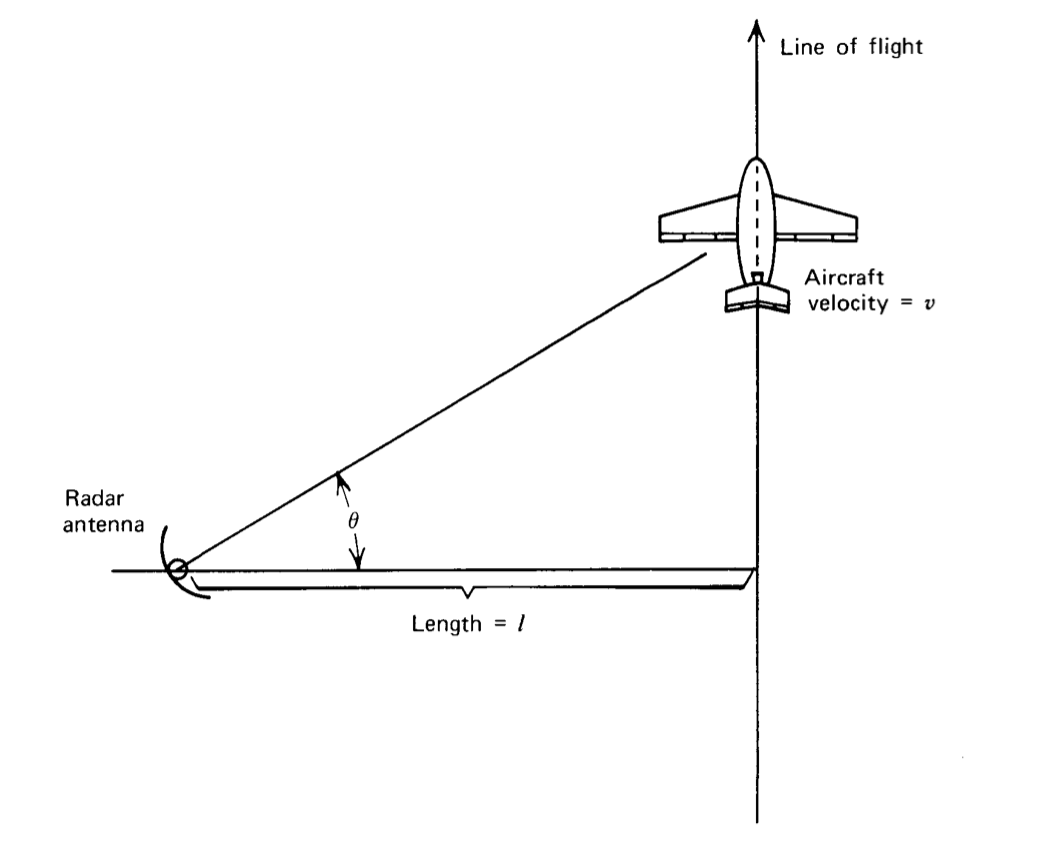
assuming that \(\theta = 0\) at \(t = 0\). This function is not transformable using our form of the Laplace transform, since it is nonzero for negative time and since no amount of time shift makes it zero for negative time. The expansion introduced in this section provides a convenient method for evaluating the performance of systems excited by transient inputs, such as Equation \(\ref{eq3.6.1}\), for which all derivatives exist at all times.
Error Series
Consider a system, initially at rest and driven by a single input, with a transfer function \(G(s)\). Furthermore, assume that \(G(s)\) can be expanded in a power series in \(s\), or that
\[G(s) = g_0 + g_1 s + g_2 s^2 + \cdots + \label{eq3.6.2} \]
If the system is excited by an input \(v_i(t)\), the output signal as a function of time is
\[v_o (t) = \mathcal{L}^{-1} [G(s) V_i (s)] = \mathcal{L} [g_0 V_i (s) + g_1 s V_i (s) + g_2 s^2 V_i (s) + \cdots +] \nonumber \]
If Equation \(\ref{eq3.6.2}\) is inverse transformed term by term, and the differentiation property of Laplace transforms is used to simplify the result, we see that(A mathematically satisfying development is given in G. C. Newton, Jr., L. A. Gould, and J. F. Kaiser, Analytical Design of Linear Feedback Controls, Wiley, New York, 1957, Appendix C. An expression that bounds the error when the series is truncated is also given in this reference.)
\[v_o (t) = g_0 v_i (t) + g_1 \dfrac{dv_i (t)}{dt} + g_t \dfrac{d^2 v_i (t)}{dt^2} + \cdots + \label{eq3.6.4} \]
The complete series yields the correct value for \(v_o(t)\) in cases where the function \(v_1(t)\) and all its derivatives exist at all times.
In practice, the method is normally used to evaluate the error (or difference between ideal and actual output) that results for a specified input. If Equation \(\ref{eq3.6.4}\) is rewritten using the error \(e(t)\) as the dependent parameter, the resultant series
\[e(t) = e_0 v_i (t) + e_1 \dfrac{dv_i (t)}{dt} + e_2 \dfrac{d^2 v_i (t)}{dt^2} + \cdots + \nonumber \]
is called an error series, and the \(e\)'s on the right-hand side of this equation are called error coefficients.
The error coefficients can be obtained by two equivalent expansion methods. A formal mathematical approach shows that
\[e_k = \dfrac{1}{k!} \dfrac{d^k}{ds^k} \left [\dfrac{V_e (s)}{V_i (s)} \right ]_{s = 0} \nonumber \]
where \(V_e (s)/ V_i (s)\) is the input-to-error transfer function for the system. Alternatively, synthetic division can be used to write the input-to-error transfer function as a series in ascending powers of \(s\). The coefficient of the sk term in this series is \(e_k\).
While the formal mathematics require that the complete series be used to determine the error, the series converges rapidly in cases of practical interest where the error is small compared to the input signal. (Note that if the error is the same order of magnitude as the input signal in a unity-feedback system, comparable results can be obtained by turning off the system.) Thus in reasonable applications, a few terms of the error series normally suffice. Furthermore, the requirement that all derivatives of the input signal exist can be usually relaxed if we are interested in errors at times separated from the times of discontinuities by at least the settling time of the system. (See Section 3.5 for a definition of settling time.)
Examples
Some important properties of feedback amplifiers can be illustrated by applying error-coefficient analysis methods to the inverting-amplifier connection shown in Figure 3.19\(a\). A block diagram obtained by assuming negligible loading at the input and output of the amplifier is shown in Figure 3.19\(b\). An error signal is generated in this diagram by comparing the actual output of the amplifier with the ideal value, \(- V_i\). The input-to-error transfer function from this block diagram is
\[\dfrac{V_e (s)}{V_i (s)} = \dfrac{-1}{1 + a(s)/2} \nonumber \]
Operational amplifiers are frequently designed to have an approximately single-pole open-loop transfer function, implying
\[a(s) \simeq \dfrac{a_0}{\tau s + 1} \nonumber \]
The error coefficients assuming this value for \(a(s)\) are easily evaluated by means of synthetic division since
\[\begin{array} {rcl} {\dfrac{V_e (s)}{V_i (s)}} & = & {\dfrac{-1}{1 + a_0/2 (\tau s + 1)} = \dfrac{-2 - 2 \tau s}{a_0 + 2 + 2 \tau s}} \\ {} & = & {-\dfrac{2}{a_0 + 2} - \dfrac{2\tau}{a_0 + 2} \left (1 - \dfrac{2}{a_0 + 2} \right ) s + \dfrac{4\tau^2}{(a_0 + 2)^2} \left (1 - \dfrac{2}{a_0 + 2} \right ) s^2 + \cdots +} \end{array} \nonumber \]

If \(a_0\), the amplifier d-c gain, is large, the error coefficients are
\[\begin{array} {rcl} {e_0} & \simeq & {-\dfrac{2}{a_0}} \\ {e_1} & \simeq & {-\dfrac{2\tau}{a_0}} \\ {e_2} & \simeq & {\dfrac{4\tau^2}{a_0^2}} \\ {} & \cdot & {} \\ {} & \cdot & {} \\ {} & \cdot & {} \\ {e_n} & = & {\dfrac{(-2)^n r^n}{a_0^n} \ \ n \ge 1} \end{array} \nonumber \]
The error coefficients are easily interpreted in terms of the loop transmis sion of the amplifier-feedback network combination in this example. The magnitude of the zero-order error coefficient is equal to the reciprocal of the d-c loop transmission. The first-order error-coefficient magnitude is equal to the reciprocal of the frequency (in radians per second) at which the loop transmission is unity, while the magnitude of each subsequent higher-order error coefficient is attenuated by a factor equal to this frequency. These results reinforce the conclusion that feedback-amplifier errors are reduced by large loop transmissions and unity-gain frequencies.
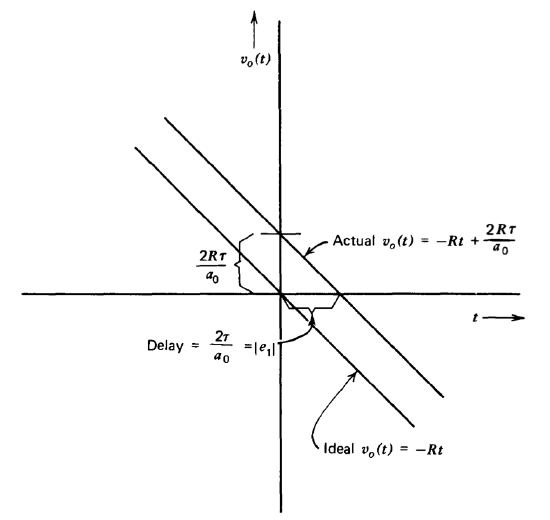
If this amplifier is excited with a ramp \(v_i (t) = Rt\), the error after any start-up transient has died out is
\[v_e (t) = e_0 v_i (t) + e_1 \dfrac{dv_i (t)}{dt} + \cdots + = -\dfrac{2Rt}{a_0} - \dfrac{2R\tau}{a_0} \nonumber \]
Because the maximum input-signal level is limited by linearity considerations, (the voltage \(Rt\) must be less than the voltage at which the amplifier saturates) the second term in the error series frequently dominates, and in these cases the error is
\[v_e (t) \simeq - \dfrac{2R \tau}{a_0} \nonumber \]
implying the actual ramp response of the amplifier lags behind the ideal output by an amount equal to the slope of the ramp divided by the unity loop-transmission frequency. The ramp response of the amplifier, assuming that the error series is dominated by the \(e_1\) term, is compared with the ramp response of a system using an infinite-gain amplifier in Figure 3.20. The steady-state ramp error, introduced earlier in Equations 3.5.5 and 3.5.11 and illustrated in Figure 3.17\(c\), is evident in this figure.
One further observation lends insight into the operation of this type of system. If the relative magnitudes of the input signal and its derivatives are constrained so that the first-order (or higher) terms in the error series dominate, the open-loop transfer function of the amplifier can be approximated as an integration.
\[a(s) \simeq \dfrac{a_0}{\tau s} \nonumber \]
In order for the output of an amplifier with this type of open-loop gain to be a ramp, it is necessary to have a constant error signal applied to the amplifier input.
Pursuing this line of reasoning further shows how the open-loop transfer function of the amplifier should be chosen to reduce ramp error. Error is clearly reduced if the quantity \(a_0/\tau\) is increased, but such an increase re quires a corresponding increase in the unity-loop-gain frequency. Unfortunately oscillations result for sufficiently high unity-gain frequencies. Alternatively, consider the result if the amplifier open-loop transfer function approximates a double integration
\[a(s) \simeq \dfrac{a_0 (\tau s + 1)}{s^2} \nonumber \]
(The zero is necessary to insure stability. See Chapter 4.) The reader should verify that both \(e_0\) and \(e_1\) are zero for an amplifier with this open-loop transfer function, implying that the steady-state ramp error is zero. Further manipulation shows that if the amplifier open-loop transfer function includes an nth order integration, the error coefficients \(e_0\) through \(e_{n - 1}\) are zero.
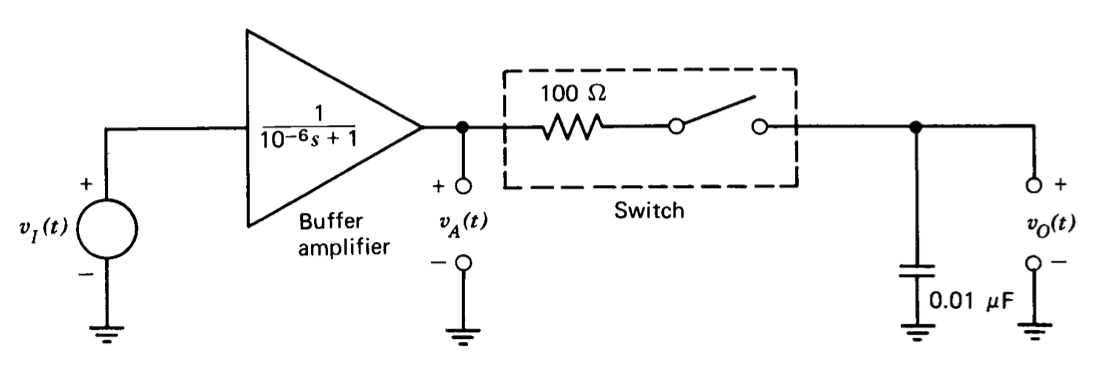
The use of error coefficients to analyze systems excited by pulse signals is illustrated with the aid of the sample-and-hold circuit shown in Figure 3.21. This circuit consists of a buffer amplifier followed by a switch and capacitor. In practice the switch is frequently realized with a field-effect transistor, and the 100-9 resistor models the on resistance of the transistor. When the switch is closed, the capacitor is charged toward the voltage \(v_I\) through the switch resistance. If the switch is opened at a time \(t_A\), the voltage \(v_O(t)\) should ideally maintain the value \(v_I(t_A)\) for all time greater than \(t_A\). The buffer amplifier is included so that the capacitor charging current is supplied by the amplifier rather than the signal source. A second buffer amplifier is often included following the capacitor to isolate it from loads, but this second amplifier is not required for the present example.
There are a variety of effects that degrade the performance of a sample-and-hold circuit. One important source of error stems from the fact that \(v_O (t)\) is generally not equal to \(v_I (t)\) unless \(v_I (t)\) is time invariant because of the dynamics of the buffer amplifier and the switch-capacitor combination. Thus an incorrect value is held when the switch is opened.
Error coefficients can be used to predict the magnitude of this tracking error as a function of the input signal and the system dynamics. For purposes of illustration, it is assumed that the buffer amplifier has a single-pole transfer function such that
\[\dfrac{V_a (s)}{V_i (s)} = \dfrac{1}{10^{-6} s + 1} \nonumber \]
Since the time constant associated with the switch-capacitor combination is also 1 \(\mu\)s, the input-to-output transfer function with the switch closed (in which case the system is linear, time-invariant) is
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{(10^{-6} s + 1)^2} \nonumber \]
With the switch closed the output is ideally equal to the input, and thus the input-to-error transfer function is
\[\dfrac{V_e (s)}{V_i (s)} = 1 - \dfrac{V_o (s)}{V_i (s)} = \dfrac{10^{-12} s^2 + 2 \times 10^{-6} s}{(10^{-6} s + 1)^2}\label{eq3.6.17} \]
The first three error coefficients associated with Equation \(\ref{eq3.6.17}\), obtained by means of synthetic division, are
\[\begin{array} {rcl} {e_0} & = & {0} \\ {e_1} & = & {2 \times 10^{-6} \text{sec}} \\ {e_2} & = & {-3 \times 10^{-12} \text{sec}^2} \end{array} \nonumber \]
Sample-and-hold circuits are frequently used to process pulses such as radar echos after these signals have passed through several amplifier stages. In many cases the pulse following amplification can be well approximated by a Gaussian signal, and for this reason a signal
\[v_i (t) = e^{-(10^{10} t^2/2)} \nonumber \]
is used as a test input.
The first two derivatives of \(v_i (t)\) are
\[\dfrac{dv_i (t)}{dt} = -10^{10} te^{-(10^{10} t^2/2)} \nonumber \]
and
\[\dfrac{d^2 v_i (t)}{dt^2} = -10^{10} e^{-(10^{10} t^2/2)} + 10^{20} t^2 e^{-(10^{10} t^2/2)} \nonumber \]
The maximum magnitude of \(dv_i/dt\) is \(6.07 \times 10^4\) volts per second occurring at \(t = \pm 10^{-5}\) seconds, and the maximum magnitude of \(d^2 v_i/dt^2\) is \(10^{10}\) volts per second squared at \(t = 0\). If the first error coefficient is used to estimate error, we find that a tracking error of approximately 0.12 volt (12% of the peak-signal amplitude) is predicted if the switch is opened at \(t = \pm 10^{-5}\) seconds. The error series converges rapidly in this case, with its second term contributing a maximum error of 0.03 volt at \(t = 0\).
PROBLEMS
Exercise \(\PageIndex{1}\)
An operational amplifier is connected to provide a noninverting gain of 10. The small-signal step response of the connection is approximately first order with a 0 to 63 %risetime of 1 \(\mu\)s. Estimate the quantity \(a(s)\) for the amplifier, assuming that loading at the amplifier input and output is insignificant.
Exercise \(\PageIndex{2}\)
The transfer function of a linear system is
\[A(s) = \dfrac{1}{(s^2 + 0.5s + 1)(0.1s + 1)} \nonumber \]
Determine the step response of this system. Estimate (do not calculate exactly) the percentage overshoot of this system in response to step excitation.
Exercise \(\PageIndex{3}\)
Use the properties of Laplace transforms to evaluate the transform of the triangular pulse signal shown in Figure 3.22.
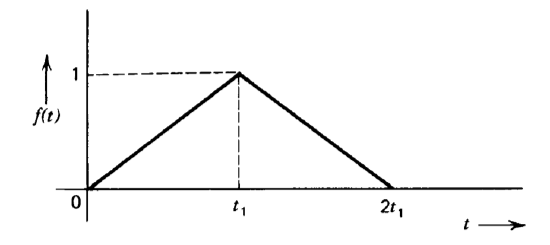
Exercise \(\PageIndex{4}\)
Use the properties of Laplace transforms to evaluate the transform of the pulse signal shown in Figure 3.23.
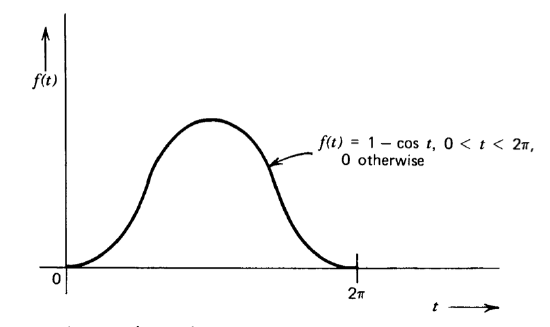
Exercise \(\PageIndex{5}\)
The response of a certain linear system is approximately second order, with a d-c gain of one. Measured performance shows that the peak value of the response to a unit step is 1.38 and that the time for the step response to first pass through one is 0.5 \(\mu\)s. Determine second-order parameters that can be used to model the system. Also estimate the peak value of the output that results when a unit impulse is applied to the input of the sys tem and the time required for the system impulse response to first return to zero. Estimate the quantities \(M_p\) and \(f_h\) for this system.
Exercise \(\PageIndex{6}\)
A high-fidelity audio amplifier has a transfer function
\[A(s) = \dfrac{100s}{(0.05s + 1) (s^2/4 \times 10^{10} + s/2 \times 10^5 + 1)(0.5 \times 10^{-6} s + 1)} \nonumber \]
Plot this transfer function in both Bode and gain-phase form. Recognize that the high- and low-frequency singularities of this amplifier are widely spaced and use this fact to estimate the following quantities when the amplifier is excited with a 10-mV step.
(a) The peak value of the output signal.
(b) The time at which the peak value occurs.
(c) The time required for the output to go from 2 to 18 V.
(d) The time until the output droops to 7.4 V.
Exercise \(\PageIndex{7}\)
An oscilloscope vertical amplifier can be modeled as having a transfer function equal to \(A_0/(10^{-9}s + 1)^5\). Estimate the 10 to 90% rise time of the output voltage when the amplifier is excited with a step-input signal.
Exercise \(\PageIndex{8}\)
An asymptotic plot of the measured open-loop frequency response of an operational amplifier is shown in Figure 3.24\(a\). The amplifier is connected as shown in Figure 3.24\(b\). (You may neglect loading.) Show that lower values of a result in more heavily damped responses. Determine the value of a that results in the closed-loop step response of the amplifier having an overshoot of 20% of final value. What is the 10 to 90% rise time in response to a step for this value of \(\alpha\)?

Exercise \(\PageIndex{9}\)
A feedback system has a forward gain \(a(s) = K/s(\tau s + 1)\) and a feed back gain \(f = 1\). Determine conditions on \(K\) and \(\tau\) so that \(e_0\) and \(e_2\) are both zero. What is the steady-state error in response to a unit ramp for this system?
Exercise \(\PageIndex{10}\)
An operational amplifier connected as a unity-gain noninverting amplifier is excited with an input signal
\[v_i (t) = 5 \tan^{-1} 10^5 t\nonumber \]
Estimate the error between the actual and ideal outputs assuming that the open-loop transfer function can be approximated as indicated below. (Note that these transfer functions all have identical values for unity-gain frequency.)
(a) \(a(s) = 10^7 /s\)
(b) \(a(s) = 10^{13} (10^{-6} s + 1)/s^2\)
(c) \(a(s) = 10^{19} (10^{-6} s + 1)^2 /s^3\)
Exercise \(\PageIndex{11}\)
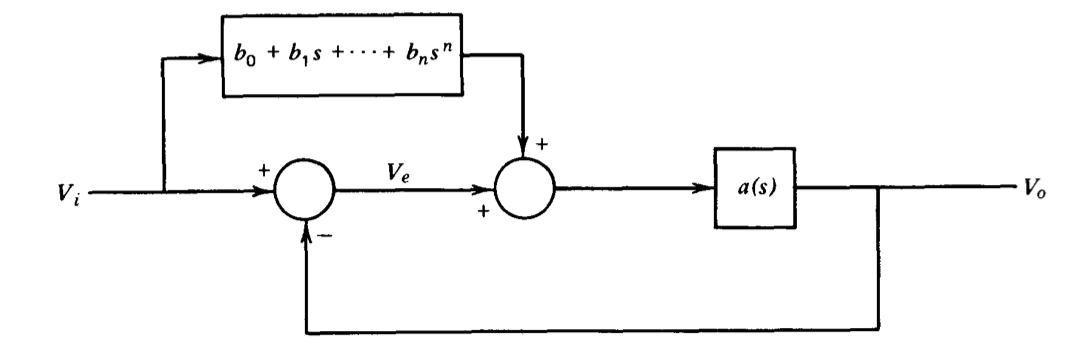
The system shown in Figure 3.25 uses a feedforward path to reduce errors. How should the \(b\)'s be chosen to reduce error coefficients \(e_0\) through \(e_n\) to zero? Can you think of any practical disadvantages to this scheme?