6.7: Operational Transconductance Amplifier
- Page ID
- 28559
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
The Operational Transconductance Amplifier, or \(OTA\) as it is normally abbreviated, is primarily used as a controlled-gain block. This means that an external controlling signal, either a current or a voltage, will be used to set a key parameter of the circuit, such as closed-loop gain or \(f_2\). This is not the same thing as the programmable op amps discussed earlier.
OTAs exhibit high output impedances. They are intended to be used as current sources. Therefore, the output voltage is a function of the output current and the load resistance. The output current is set by the differential input signal and the OTA's transconductance. Transconductance is, in turn, controlled by a setup current, \(I_{abc}\). What this all means is that the output signal is a function of \(I_{abc}\). If \(I_{abc}\) is increased, transconductance rises and with it, output voltage. Normally, OTAs are operated without feedback. One major consequence of this is that the differential input signal must remain relatively small in order to avoid distortion. Typically, the input signal remains below 100 mV peak to peak.
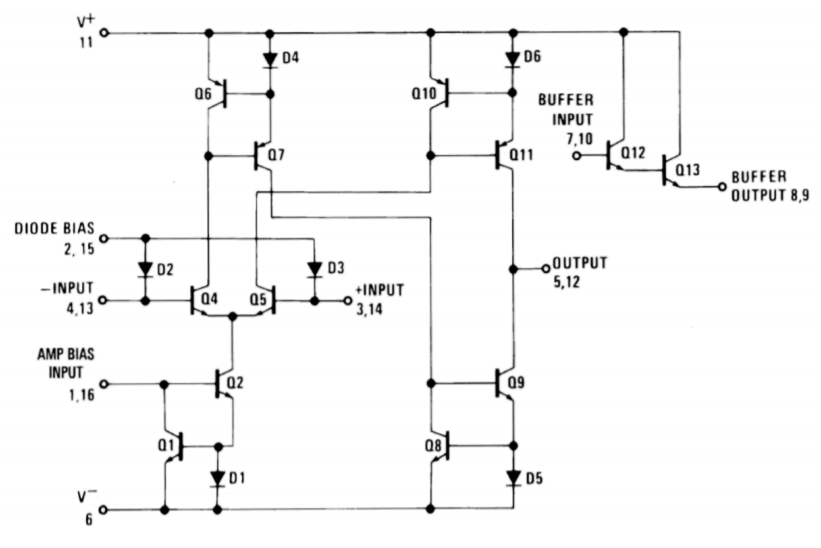
Figure \(\PageIndex{1}\): LM13700 equivalent circuit. Reprinted courtesy of Texas Instrutments
One of the first popular OTAs was the 3080. An improved version of this chip is the LM13700. It features two amplifiers in a single package. Because OTAs are modeled as output current sources, the LM13700 includes simple emitter follower buffers for each OTA. Connection to the buffers is optional. Also included are inputl inearizing diodes that allow higher input levels, and thus, superior signal-to-noise performance. The schematic of the LM13700 is shown in Figure \(\PageIndex{1}\). The differential amplifier stage comprised of \(Q_4\) and \(Q_5\) is biased by \(Q_2\). The current set by \(Q_2\) establishes the transconductance of this stage. \(Q_2\) is part of a current mirror made along with \(Q_1\) and \(D_1\). \(Q_2\) mirrors the current flowing through \(Q_1\). The current flowing through \(Q_1\) is \(I_{abc}\), and is set externally. Thus, the differential amplifier is directly controlled by the external current.
Example \(\PageIndex{1}\)
One example of OTA use is shown in Figure \(\PageIndex{2}\). This circuit is a simple voltage-controlled amplifier (VCA). Let's walk through the circuit to see how the component values were derived.
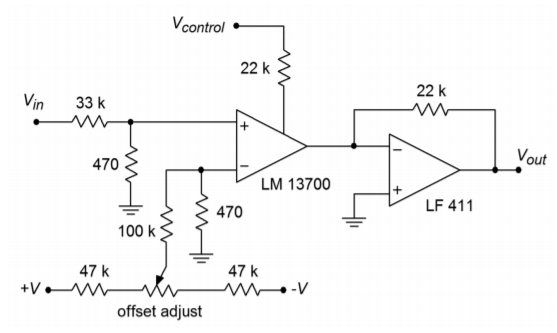
Figure \(\PageIndex{2}\): Voltage-controlled amplifier.
The gain of the system is set by \(V_{control}\). The 22 k\(\Omega\) resistor is used to turn \(V_{control}\) into \(I_{abc}\). The maximum value for \(I_{abc}\) is specified as 1 mA. By referring to Figure 6.3.4, an expression for the maximum \(I_{abc}\) may be determined from Ohm's Law.
\[ I_{abc} = \frac{V_{+} −V_{-} − V_{D1}}{R_{control}} \nonumber \]
\[ I_{abc} = \frac{5−(−5)−0.7}{22 k} \nonumber \]
\[ I_{abc} = 423\mu A \nonumber \]
This places us at about half the allowed maximum, giving a twofold safety margin. The LM13700 transconductance graph indicates that we may expect a maximum value of about 10 milliSiemens with our maximum \(I_{abc}\). Note how the input signal must be attenuated in order to prevent overload. For reasonable distortion levels the input to the LM13700 should be below 50 mV peak to peak. This is accomplished by the 33 k\(\Omega\)/470 \(\Omega\) voltage divider. This divider produces an input impedance of approximately 33 k\(\Omega\), and a loss factor of
\[ Loss = \frac{470}{33 k+470} \nonumber \]
\[ Loss = 0.014 \nonumber \]
This means that the circuit may amplify peak to peak signals as large as
\[ 50 mV = V_{in-max} Loss \nonumber \]
\[ V_{in-max} = \frac{50 mV}{Loss} \nonumber \]
\[ V_{in-max} = 3.56 V \nonumber \]
The current out of the LM13700 drives an LF411 configured as a current-to-voltage converter. The transresistance of this portion is 22 k\(\Omega\). Using the maximum 50 mV input, the maximum output signal will be
\[ I_{out -13700} = V_{in-13700} g_m \nonumber \]
\[ I_{out -13700} = 50 mV\times 10 ms \nonumber \]
\[ I_{out -13700} = 500\mu A \nonumber \]
This current will drive the LF411 to a maximum output of
\[ V_{out} = I_{out -13700} R_f \nonumber \]
\[ V_{out} = 500\mu A\times 22 k \nonumber \]
\[ V_{out} = 11 V \nonumber \]
With the signals shown, this circuit acts as a simple amplitude modulator. The \(V_{control}\) signal is impressed upon the input signal. These are the audio and carrier signals, respectively. This setup can also be used as part of an AGC (automatic gain control) loop. Also, note the adjustable DC signal applied to the inverting input. This is used to null the amplifier. This is an important point. Any DC offset is also affected by the gain change, in effect causing the control signal to “leak” into the output. This can produce many undesirable side effects, including clicking and popping noises if the circuit is used as an audio VCA. By nulling the output offset, these effects are eliminated. In order to keep the inputs balanced, a 470\(\Omega\) is added to the inverting input. Now, each input sees approximately 470 \(\Omega\) to ground.
When designing a VCA such as in the prior example, you usually start with known maximum input and output voltages. The feedback resistor of the current-to-voltage converter is chosen to yield the desired maximum output potential when the OTA is producing its maximum output current. The OTA's maximum input potential times its transconductance will yield the OTA's maximum output current. Once this current has been established, the value of \(R_{control}\) may be determined given the range of \(V_{control}\). The maximum allowable OTA input potential is determined from the OTA distortion graph, and in association with the desired maximum input voltage, dictates the ratio of the input voltage divider.
OTAs may also be used to create voltage-controlled filters (VCF), where the cutoff frequency is a function of \(V_{control}\). Discussion of filters in general is found in Chapter Eleven. OTAs lend themselves to several unique applications. The down side is that they have limited dynamic range. That is, the range of signal amplitudes that they can handle without excessive distortion or noise is not as great as it is in many other devices.


