6.8: Norton Amplifier
- Page ID
- 28560
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is possible to create an input-differencing function without using a differential amplifier. One alternative is to use a current mirror arrangement to form a current differencing amplifier. Because the input function deals with a difference of current instead of voltage, amplifiers of this type are often referred to as Norton amplifiers. Norton amplifiers have the distinct advantages of low cost and the ability to operate from a single-polarity power supply. Perhaps the most popular Norton amplifier is the LM3900. The LM3900 is a quad device, meaning that four amplifiers are combined in a single package.
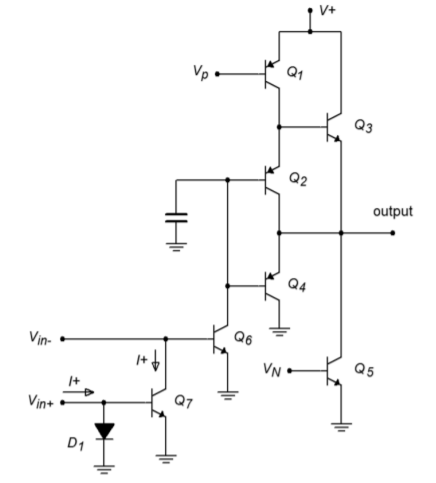
Figure \(\PageIndex{1}\): a. LM3900 schematic (left). b. schematic symbol (below)
The internal circuitry of one Norton amplifer is shown in Figure \(\PageIndex{1a}\). Norton amplifiers also use a slightly modified schematic symbol, shown in Figure \(\PageIndex{1b}\), to distinguish them from ordinary op amps. The amplifier is comprised of two main sections: a current-differencing input portion consisting of \(Q_6\), \(Q_7\), and \(D_1\), and a gain stage comprising \(Q_1\) through \(Q_5\). The current-differencing portion is of greatest interest to us, and is based upon the current mirror concept. \(D_1\) and \(Q_7\) make up a current mirror that is fed by the noninverting input's source current, \(I_{+}\). This current flows down through \(D_1\), and is mirrored into \(Q_7\). Therefore, the collector current of \(Q_7\) is equal to \(I_{+}\). This current is effectively subtracted from the current that enters the inverting input. The differential current, \(I_{-} - I_{+}\), is the net input current that feeds \(Q_{6}\), and is amplified by the following stage. Note how the schematic symbol of Figure \(\PageIndex{1b}\) echoes the current mirror subtraction process.
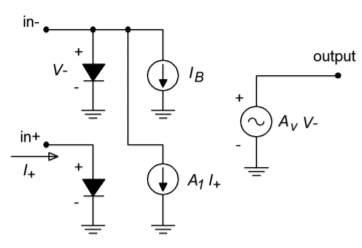
Figure \(\PageIndex{2}\): Norton equivalent circuit.
Due to its unique input configuration, the equivalent model of the Norton amplifier is rather different from the standard op amp. This is illustrated in Figure \(\PageIndex{2}\). This clearly shows that the Norton amplifier is a current-sensing device. Also, note that the input impedance for the noninverting input is little more than the dynamic resistance of \(D_{+}\). This resistance is dependent on the input current, and may be found using the standard diode resistance equation
\[ Z_{in +} = \frac{26 mV}{I_{+}} \label{6.12} \]
Another important point is that both the inverting and noninverting inputs are locked at approximately one diode drop above ground. This can be beneficial for a current summing node, but it does require that some form of input resistor be used if a voltage input is expected. A side benefit of this is that given a large enough input resistor, there is virtually no limit to the input common-mode voltage range as the potential will drop across the input resistor. For proper AC operation, an appropriate biasing current must be used. A typical inverting amplifier is shown in Figure \(\PageIndex{3}\).
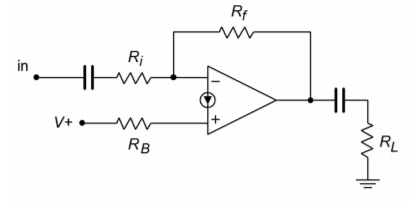
Figure \(\PageIndex{3}\): Typical inverting amplifier.
Note the input and output coupling capacitors, as well as \(R_B\), that serves to convert the bias voltage into a bias current. A generalized model of this circuit is shown in Figure \(\PageIndex{4}\). From this, we will be able to determine a voltage gain expression, and a technique for determining a proper value for \(R_B\).
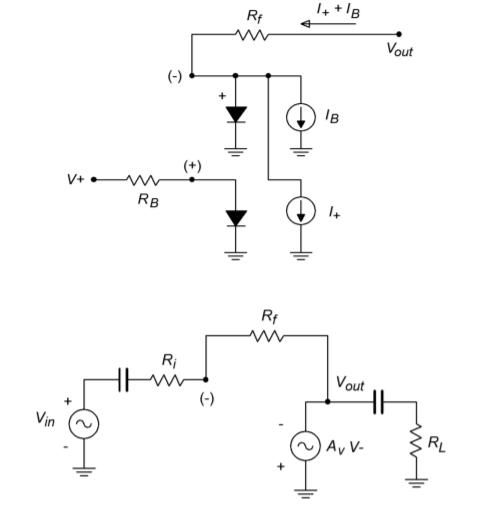
Figure \(\PageIndex{4}\): Generalized model of the amplifier in Figure \(\PageIndex{3}\). a. Bias equivalent (top). b. AC equivalent (bottom).
We'll start by setting up an expression for the output voltage for the bias equivalent.
\[ V_{out} = V_{D -} + R_f (I_{+} + I_{B}) \nonumber \]
and,
\[ I_{+} = \frac{V_{supply} − V_{D+}}{R_B} \nonumber \]
Combining the above two equations yields
\[ V_{out} = V_{D-} + R_f (\frac{V_{supply} − V_{D+}}{R_B} + I_B) \label{6.13} \]
Normally, \(V_{supply} \gg V_D\), and \(I_B\) is relatively small. Given these factors, \ref{6.13} may be approximated as
\[ V_{out} = V_{supply} \frac{R_f}{R_B} \label{6.14} \]
Therefore, for a midpoint bias,
\[ R_B = 2 R_f \label{6.15} \]
For the AC equivalent circuit, the gain Equation may be derived in the same fashion as it was in Chapter Four for a standard inverting op amp configuration.
\[ A_v = − \frac{R_f}{R_i} \label{6.16} \]
As in the standard op amp inverting amplifier, the input impedance may be approximated as \(R_i\).
Example \(\PageIndex{1}\)
Using the LM3900, design an amplifier that operates from a single +9 V battery, has an inverting voltage gain of 20, an input impedance of at least 50 k\(\Omega\), and a lower break frequency of no more than 100 Hz.
First, \(R_i\) may be established from the input impedance spec at 50 k\(\Omega\). From here, both \(R_f\) and \(R_B\) may be determined.
\[ A_v =− \frac{R_f}{R_i} \nonumber \]
\[ R_f =−A_v R_i \nonumber \]
\[ R_f =−(−20)\times 50 k \Omega \nonumber \]
\[ R_f = 1 M\Omega \nonumber \]
\[ R_B = 2 R_f \nonumber \]
\[ R_B = 2\times 1 M\Omega \nonumber \]
\[ R_B = 2 M\Omega \nonumber \]
The input coupling capacitor will be used to set the lower break frequency in association with \(R_i\). This is basically unchanged from the single-supply bias calculations presented in Chapter Four.
\[ f_c = \frac{1}{2 \pi RC} \nonumber \]
\[ C = \frac{1}{2 \pi R f_c} \nonumber \]
\[ C = \frac{1}{2 \pi 50 k 100 Hz} \nonumber \]
\[ C = 31.8 nF \nonumber \]
The completed circuit is shown in Figure \(\PageIndex{5}\). Although this circuit does not detail the output coupling capacitor and load resistance, it would be handled in a similar vein.
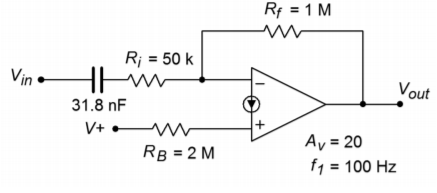
Figure \(\PageIndex{5}\): Completed design.
Computer Simulation
A Multisim simulation of the amplifier of Example \(\PageIndex{1}\) is shown in Figure \(\PageIndex{6}\). A simple coupling network has been added to the output. The critical frequency of the output network is approximately 1.6 Hz, well below the input network. In this way, the input network is clearly dominant, and its effect on the system lower frequency response can be seen clearly. The AC Analysis is plotted from 1 Hz to 10 kHz. The midband gain is approximately 26 dB, yielding an ordinary gain of 20 as desired. The lower end of the frequency response begins to roll off below 200 Hz, reaching approximately 23 dB (i.e., 3 dB down) at the target frequency of 100 Hz. The response continues its constant descent to the lower limit of the graph. Only a slight increase in slope may be noted in the 1 to 2 Hz region. If the frequency range is extended another decade lower, the effect of the output coupling network will be more obvious.
One possible problem with the circuit presented in Example \(\PageIndex{1}\) is that any power supply ripple present on \(V_{supply}\) will be passed into the amplifier via \(R_B\), and appear at the output. In order to minimize this problem, a power supply decoupling circuit such as that presented in Chapter Four may be used.
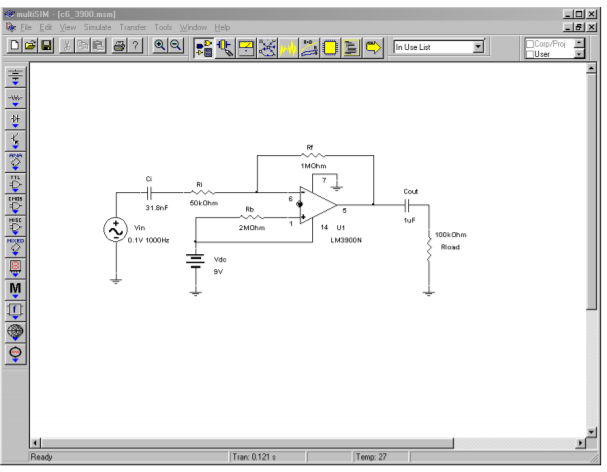
Figure \(\PageIndex{6a}\): Simulation of LM3900 amplifier.
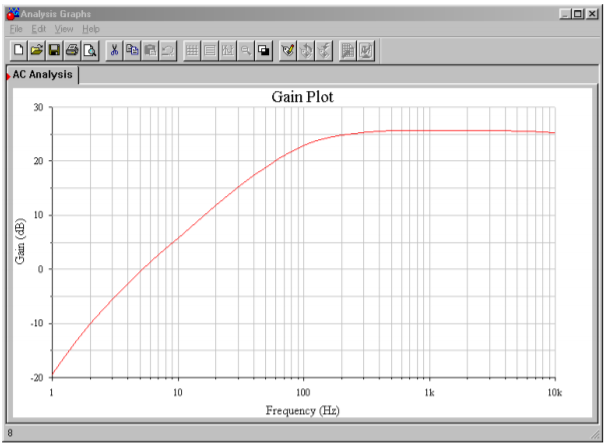
Figure \(\PageIndex{6b}\): Gain plot for LM3900 amplifier.
Figure \(\PageIndex{7}\) shows a typical inverting amplifier with a decoupling circuit added. Note that \(R_B\) is not set to twice \(R_f\), but rather, is set equal to it. This is because \(R_B\) is only being driven by one half of the supply voltage due to the lower resistance decoupling divider.
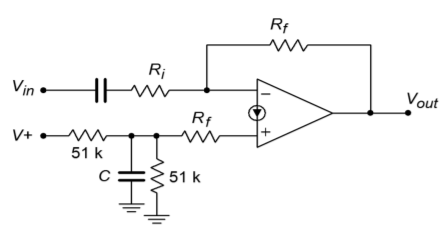
Figure \(\PageIndex{7}\): Optimized bias circuitry.
Norton amplifiers may be used in a variety of other configurations as well, including noninverting and differential amplifiers. A simple noninverting amplifier is shown in Figure \(\PageIndex{8}\). Unlike the ordinary op amp version, the Norton amplifier requires an input resistor. Remembering that the input impedance of the noninverting input may be quite low (Equation \ref{6.12}), we can derive equations for both circuit input impedance and voltage gain.
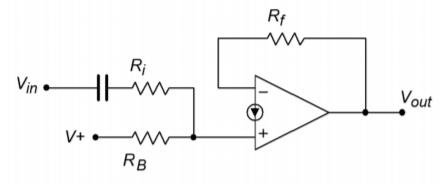
Figure \(\PageIndex{8}\): Noninverting amplifier.
The input impedance is the series combination of \(R_i\) and the impedance looking into the noninverting input, \(Z_{in+}\).
\[ Z_{in} = R_i + Z_{in+} \label{6.17} \]
In order to find voltage gain, note that due to the virtual ground at the inverting input, the drop across \(R_f\) is equivalent to \(V_{out}\).
\[ V_{out} = V_{Rf} = R_f I_{-} \label{6.18} \]
\(V_{in}\) drops across the system input impedance. Given Equation \ref{6.17}, we may say
\[ V_{in} = I_{+} (R_i+Z_{in+}) \label{6.19} \]
Because, by definition, \(A_v = V_{out}/V_{in}\), we may say
\[ A_v = \frac{R_f I_{-}}{I_{+} (R_i + Z_{in+})} \nonumber \]
The two currents are identical in the AC equivalent circuit, so this simplifies to
\[ A_v = \frac{R_f}{R_i + Z_{in+}} \label{6.20} \]
In summary, there are a few things that you should remember about Norton amplifiers:
- The inputs are current-sensing, and thus, require some form of input-current limiting resistance.
- As with an ordinary op amp, voltage gain is set by the two feedback resistors.
- A DC bias potential must be fed into the noninverting input via a current limiting resistor, \(R_B\). This resistor is normally twice the size of \(R_f\).


