3.6: Sinusoidal Steady State and the Series RLC Circuit
- Page ID
- 9966
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Phasors may be used to analyze the behavior of electrical and mechanical systems that have reached a kind of equilibrium called sinusoidal steady state. In the sinusoidal steady state, every voltage and current (or force and velocity) in a system is sinusoidal with angular frequency \(ω\). However, the amplitudes and phases of these sinusoidal voltages and currents are all different. For example, the voltage across a resistor might lead the voltage across a capacitor by 90∘ (\(\frac π 2\) radians) and lag the voltage across an inductor by 90∘ (\(\frac π 2\) radians).
In order to make our application of phasors to electrical systems concrete, we consider the series RLC circuit illustrated in Figure \(\PageIndex{1}\). The arrow labeled \(i(t)\) denotes a current that flows in response to the voltage applied, and the + and - on the voltage source indicate that the polarity of the applied voltage is positive on the top and negative on the bottom. Our convention is that current flows from positive to negative, in this case clockwise in the circuit.
We will assume that the voltage source is an audio oscillator that produces the voltage
\[V(t)=A\cos(ωt+φ) \nonumber \]
We represent this voltage as the complex signal
\[V(t)↔Ae^{jφ}e^{jωt} \nonumber \]
and give it the phasor representation
\[V(t)↔V;V=Ae^{jφ} \nonumber \]
We then describe the voltage source by the phasor V and remember that we can always compute the actual voltage by multiplying by \(e^{jωt}\) and taking the real part:
\[V(t)=\mathrm{Re}\{Ve^{jωt}\} \nonumber \]
Show that
\[\mathrm{Re}[Ve^{jωt}]=A\cos(ωt+φ) \nonumber \]
when \(V=Ae^{jφ}\).
Circuit Laws
In your circuits classes you will study the Kirchhoff laws that govern the low frequency behavior of circuits built from resistors (R), inductors (L), and capacitors (C). In your study you will learn that the voltage dropped across a resistor is related to the current that flows through it by the equation
\[V_R(t)=Ri(t) \nonumber \]
You will learn that the voltage dropped across an inductor is proportional to the derivative of the current that flows through it, and the voltage dropped across a capacitor is proportional to the integral of the current that flows through it:
\[V_L(t)=L\frac {di} {dt} (t) \nonumber \]
\[V_C(t)=\frac 1 C ∫i(t)dt \nonumber \]
Phasors and Complex Impedance
Now suppose that the current in the preceding equations is sinusoidal, of the form
\[i(t)=B\cos(ωt+θ) \nonumber \]
We may rewrite \(i(t)\) as
\[i(t)=\mathrm{Re}\{Ie^{jωt}\} \nonumber \]
where \(I\) is the phasor representation of \(i(t)\).
Find the phasor \(I\) in terms of \(B\) and \(θ\) in the above Equation.
The voltage dropped across the resistor is
\[\begin{align} V_R(t) &=Ri(t) \\[4pt] &=R\mathrm{Re}\{Ie^{jωt}\} \\[4pt] &=\mathrm{Re}\{RIe^{jωt}\} \end{align} \nonumber \]
Thus the phasor representation for \(V_R(t)\) is
\[V_R(t)↔V_R;V_R=RI \nonumber \]
We call R the impedance of the resistor because R is the scale constant that relates the “phasor voltage VR' to the “phasor current I.”
The voltage dropped across the inductor is
\[V_L(t)=L\frac {di}{dt}(t)=L\frac d {dt}\mathrm{Re}\{Ie^{jωt}\} \nonumber \]
The derivative may be moved through the Re[] operator (see Exercise) to produce the result
\[\begin{align} V_L(t)&=L\mathrm{Re}\{jωIe^{jωt}\} \\[4pt] &=\mathrm{Re}\{jωLIe^{jωt}\} \end{align} \nonumber \]
Thus the phasor representation of \(V_L(t)\)
\[V_L(t)↔V_L;V_L=jωLI \nonumber \]
We call \(jωL\) the impedance of the inductor because \(jωL\) is the complex scale constant that relates “phasor voltage \(V_L\)' to “phasor current \(I\).
Prove that the operators \(\frac d {dt}\) and Re[] commute:
\(\frac d {dt}\mathrm{Re}\{e^{jωt}\}=\mathrm{Re}\{\frac d {dt} e^{jωt}\}\)
The voltage dropped across the capacitor is
\[V_C(t)=\frac 1 C ∫i(t)dt = \frac 1 C ∫ \mathrm{Re}\{Ie^{jωt}\}dt \nonumber \]
The integral may be moved through the Re[] operator to produce the result
\[ \begin{align} V_C(t) &=\frac 1 C \mathrm{Re}\{\frac I {jω} e^{jωt}\} \\[4pt] &=\mathrm{Re}\{\frac I {jωC} e^{jωt}\} \end{align} \nonumber \]
Thus the phasor representation of VC(t) is
\[V_C(t)↔V_C;V_C=\frac I {jωC} \nonumber \]
We call \(\frac 1 {jωC}\) the impedance of the capacitor because \(\frac 1 {jωC}\) is the complex scale constant that relates “phasor voltage VC" to “phasor current I.”
Kirchhoff's Voltage Law
Kirchhoff's voltage law says that the voltage dropped in the series combination of R, L, and C illustrated in Figure equals the voltage generated by the source (this is one of two fundamental conservation laws in circuit theory, the other being a conservation law for current):
\[V(t)=V_R(t)+V_L(t)+V_C(t) \nonumber \]
If we replace all of these voltages by their complex representations, we have
\[\mathrm{Re}\{Ve^{jωt}\}=\mathrm{Re}\{(V_R+V_L+V_C)e^{jωt}\} \nonumber \]
An obvious solution is
\[V=VR+VL+VC \nonumber \]
\[=(R+jωL+\frac 1 {jωC})I \nonumber \]
where I is the phasor representation for the current that flows in the circuit. This solution is illustrated in the Figure, where the phasor voltages \(RI\), \(jωLI\), and \(\frac 1 {jωC} I\) are forced to add up to the phasor voltage \(V\).
Redraw the above Figure for \(R=ωL=\frac 1 {ωC} = 1\)
Impedance
We call the complex number \(R+jωL+\frac 1 {jωC}\) the complex impedance for the series RLC network because it is the complex number that relates the phasor voltage V to the phasor current I:
\[V=ZI \nonumber \]
\[Z=R+jωL+\frac 1 {jωC} \nonumber \]
The complex number \(Z\) depends on the numerical values of resistance \((R)\), inductance \((L)\), and capacitance \((C)\), but it also depends on the angular frequency \((ω)\) used for the sinusoidal source. This impedance may be manipulated as follows to put it into an illuminating form:
\[Z=R+j(ωL−\frac 1 {ωC}) \nonumber \]
\[= R+j \sqrt{\frac L C}(ω \sqrt{LC}−\frac 1 {/sqrt{ωLC}}) \nonumber \]
The parameter \(ω_0=\frac 1 {\sqrt{LC}}\) is a parameter that you will learn to call an "undamped natural frequency" in your more advanced circuits courses. With it, we may write the impedance as
\[Z=R+jω_0L(\frac ω {ω_0}−\frac {ω_0} ω) \nonumber \]
The frequency \(\frac ω {ω_0}\) is a normalized frequency that we denote by \(ν\). Then the impedence, as a function of normalized frequency, is
\[Z(ν)=R+jω_0L(ν−\frac 1 ν) \nonumber \]
When the normalized frequency equals one \((ν=1)\), then the impedance is entirely real and \(Z=R\). The circuit looks like it is a single resistor.
\[∣Z(ν)∣∣=R[1+(/frac {ω_0L} R)^2(ν−\frac 1 ν)^2]^{1/2} \nonumber \]
\[\mathrm{arg}Z(ν)=\tan^{−1}\frac {ω_0L} R (ν−\frac 1 ν) \nonumber \]
The impedance obeys the following symmetries around \(ν=1\):
\[Z(ν)=Z^∗(\frac 1 ν) \nonumber \]
\[∣Z(ν)∣=∣Z(\frac 1 ν)∣ \nonumber \]
\[\mathrm{arg}Z(ν)=−\mathrm{arg}Z(\frac 1 ν) \nonumber \]
In the next paragraph we show how this impedance function influences the current that flows in the circuit.
Resonance
The phasor representation for the current that flows the current that flows in the series RLC circuit is
\[\begin{align} I &=VZ(ν) \\[4pt] &=1|Z(ν)|e−jargZ(ν)V \end{align} \nonumber \]
The function \(H(ν)=\frac 1 {Z(ν)}\) displays a "resonance phenomenon." that is, \(|H(ν)|\) peaks at \(ν=1\) and decreases to zero and ν=0 and ν=∞:
\[|H(ν)|= \begin{cases} 0, ν=0 \\ \frac 1 R, ν=1 \\ 0, ν=∞ \end{cases} \nonumber \]
When \(|H(ν)|=0\), no current flows.
The function \(|H(ν)|\) is plotted against the normalized frequency \(ν=\frac ω {ω_0}\) in the Figure. The resonance peak occurs at ν=1, where \(|H(ν)|=\frac 1 R\) meaning that the circuit looks purely resistive. Resonance phenomena underlie the frequency selectivity of all electrical and mechanical networks.

(MATLAB) Write a MATLAB program to compute and plot \(|H(ν)|\) and \(argH(ν)\) versus ν for ν ranging from 0.1 to 10 in steps of 0.1. Carry out your computations for \(ω_0LR=10,1,0.1\), and 0.01, and overplot your results.
Circle Criterion and Power Factor
Our study of the impedance \(Z(ν)\) and the function \(H(ν)=\frac 1 {Z(ν)}\) brings insight into the resonance of an RLC circuit and illustrates the frequency selectivity of the circuit. But there is more that we can do to illuminate the behavior of the circuit.
\[V=RI+j(ωL−\frac 1 {ωC})I \nonumber \]
This equation shows how voltage is divided between resistor voltage RI and inductor-capacitor voltage \(j(ωL−1ωC)I\).
\[V=RI+jω_0L(\frac ω {ω_0}−\frac {ω_0} ω)I \nonumber \]
or
\[V=RI+\frac {jω_0L} R (ν−/frac 1 ν)RI \nonumber \]
In order to simplify our notation, we can write this equation as
\[V=V_R+jk(ν)V_R \nonumber \]
where \(V_R\) is the phasor voltage \(RI\) and \(k(ν)\) is the real variable
\[k(ν)=\frac {ω_0L} R (ν−\frac 1 ν) \nonumber \]
The equation brings very important geometrical insights. First, even though the phasor voltage \(V_R\) in the RLC circuit is complex, the terms \(V_R\) and \(jk(ν)V_R\) are out of phase by \(\frac π 2\) radians. This means that, for every allowable value of \(V_R\), the corresponding \(jk(ν)V_R\) must add in a right triangle to produce the source voltage V. This is illustrated in Figure. As the frequency ν changes, then \(k(ν)\) changes, producing other values of \(V_R\) and \(jk(ν)V_R\) that sum to V. Several such solutions for \(V_R\) and \(jk(ν)V_R\) are illustrated in Figure 3.15(b). From the figure we gain the clear impression that the phasor voltage \(V_{>R}\) lies on a circle of radius \(\frac V 2\) centered at \(\frac V 2\) Let's try this solution,
\[V_R=\frac V 2 +\frac V 2 e^{jψ}=\frac V 2 (1+e^{jψ}) \nonumber \]
and explore its consequences. When this solution is substituted into Equation, the result is
\[V=\frac V 2 (1+e^{jψ})+jk(ν)V_2(1+e^{jψ}) \nonumber \]
or
\[2=(1+e^{jψ})[1+jk(ν)] \nonumber \]
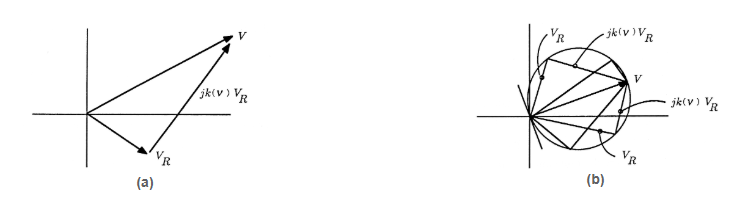
If we multiply the left-hand side by its complex conjugate and the right-hand side by its complex conjugate, we obtain the identity
\[4=2(1+\cosψ)[1+k^2(ν)] \nonumber \]
This equation tells us how the angle ψ depends on \(k(ν)\) and, conversely, how \(k(ν)\) depends on ψ:
\[\cosψ = \frac {1−k^2(ν)} {1+k^2(ν)} \nonumber \]
\[k^2(ν)=\frac {1−\cosψ} {1+\cosψ} \nonumber \]
The number \(\cosψ\) lies between −1 and +1, so a circular solution does indeed work.
Check \(−1≤\cosψ≤1\) for \(−∞<k<∞\) and \(−∞<k<∞\) for \(−π≤ψ≤π\). Sketch \(k\) versus \(ψ\) and \(ψ\) versus \(k\).
The equation \(V_R=\frac V 2 (1+e{jψ})\) is illustrated in Figure. The angle that \(V_R\) makes with \(V\) is determined from the equation
\[2φ+π−ψ=π⇒φ=\frac ψ 2 \nonumber \]
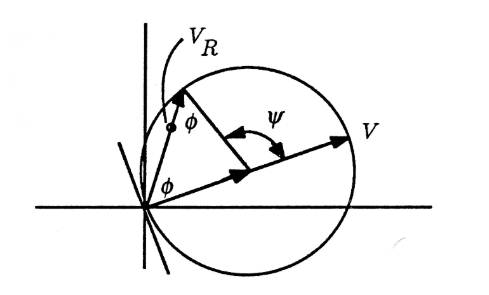
In the study of power systems, cosφ is a "power factor" that determines how much power is delivered to the resistor. We may denote the power factor as
\[η=\cosφ=\cos\frac ψ 2 \nonumber \]
But \(\cosψ\) may be written as
\[η=cosφ=cos\frac ψ 2 \nonumber \]
But \(\cosψ\) may be written as
\[\begin{align} \cosψ=\cos(φ+φ) &= \cos^2φ−−\sin^2φ \\ &=\cos^2φ−(1−\cos^2φ) \\ &=2\cos^2φ−1 \\ &=2η^2−1 \end{align} \nonumber \]
Therefore the square of the power factor η is
\[ \eta ^2 = \frac{\cos \psi + 1}{2} = \frac{1}{1+k^2(\nu)} \nonumber \]
The power factor is a maximum of 1 for \(k(ν)=0\), corresponding to \(ν=1(ω=ω_0)\). It is a minimum of 0 for \(k(ν)=±∞\), corresponding to \(ν=0,∞(ω=0,∞)\).
With \(k\) defined as \(k(ν)=\frac {ω_0L} R (ν−\frac 1 ν)\), plot \(k^2(ν)\), \(\cosψ\), and \(η^2\) versus \(ν\).
Find the value of \(ν\) that makes the power factor \(η=0.707\).


