4.5: Projections

Orthogonality

When the angle between two vectors is \(\frac π 2\) or \(90^0\), we say that the vectors are orthogonal. A quick look at the definition of angle (Equation 12 from "Linear Algebra: Direction Cosines") leads to this equivalent definition for orthogonality:

\[(x,y)=0⇔x\; \mathrm{and}\;y\;\mathrm{are\;orthogonal}. \nonumber \]

For example, in Figure 1(a), the vectors \(x=\begin{bmatrix}3\\1\end{bmatrix}\) and \(y=\begin{bmatrix}-2\\6\end{bmatrix}\) are clearly orthogonal, and their inner product is zero:

\[(x,y)=3(−2)+1(6)=0 \nonumber \]

In Figure 1(b), the vectors \(x=\begin{bmatrix}3\\1\\0\end{bmatrix}\), \(y=\begin{bmatrix}−2\\6\\0\end{bmatrix}\), and \(z=\begin{bmatrix}0\\0\\4\end{bmatrix}\) are mutually orthogonal, and the inner product between each pair is zero:

\[(x,y)=3(−2)+1(6)+0(0)=0 \nonumber \]

\[(x,z)=3(0)+1(0)+0(4)=0 \nonumber \]

\[(y,z)=−2(0)+6(0)+0(4)=0 \nonumber \]

(a)

(b)

Figure \(\PageIndex{1}\): Orthogonality of Vectors.

Exercise \(\PageIndex{1}\)

Which of the following pairs of vectors is orthogonal:

1. \(x=\begin{bmatrix}1\\0\\1\end{bmatrix},y=\begin{bmatrix}0\\1\\0\end{bmatrix}\)
2. \(x=\begin{bmatrix}1\\1\\0\end{bmatrix},y=\begin{bmatrix}1\\1\\1\end{bmatrix}\)
3. \(x=e_1,y=e_3\)
4. \(x=\begin{bmatrix}a\\b\end{bmatrix} , y=\begin{bmatrix}−b\\a\end{bmatrix}\)

We can use the inner product to find the projection of one vector onto another as illustrated in Figure 2. Geometrically we find the projection of \(x\) onto \(y\) by dropping a perpendicular from the head of \(x\) onto the line containing \(y\). The perpendicular is the dashed line in the figure. The point where the perpendicular intersects \(y\) (or an extension of \(y\)) is the projection of \(x\) onto \(y\), or the component of \(x\) along \(y\). Let's call it \(z\).

Figure \(\PageIndex{2}\): Component of One Vector along Another

Exercise \(\PageIndex{1}\)

Draw a figure like Figure 2 showing the projection of y onto x.

The vector \(z\) lies along \(y\), so we may write it as the product of its norm \(||z||\) and its direction vector \(u_y\) :

\[z=||z||u_y=||z||\frac {y} {||y||} \nonumber \]

But what is norm \(||z||\)? From Figure 2 we see that the vector \(x\) is just \(z\), plus a vector \(v\) that is orthogonal to \(y\):

\[x=z+v,(v,y)=0 \nonumber \]

Therefore we may write the inner product between \(x\) and \(y\) as

\[(x,y)=(z+v,y)=(z,y)+(v,y)=(z,y) \nonumber \]

But because \(z\) and \(y\) both lie along \(y\), we may write the inner product \((x,y)\) as

\[(x,y)=(z,y)=(||z||u_y,||y||u_y)=||z||||y||(u_y,u_y)=||z||||y||||u_y||^2=||z||||y|| \nonumber \]

From this equation we may solve for \(||z||=(x,y)||y||\) and substitute \(||z||\) into Equation \(\PageIndex{6}\) to write \(z\) as

\[z=||z||\frac y {||y||}=\frac {(x,y)}{||y||} \frac y {||y||}= \frac {(x,y)}{(y,y)}y \nonumber \]

Equation \(\PageIndex{10}\) is what we wanted–an expression for the projection of \(x\) onto \(y\) in terms of \(x\) and \(y\).

Exercise \(\PageIndex{1}\)

Show that \(||z||\) and \(z\) may be written in terms of \(\cosθ\) for \(θ\) as illustrated in Figure 2:

\(||z||=||x||\cosθ\)

\(z=\frac {||x||\cosθ}{||y||}y\)

Orthogonal Decomposition

You already know how to decompose a vector in terms of the unit coordinate vectors,

\[\mathrm{x}=\left(\mathrm{x}, \mathrm{e}_{1}\right) \mathrm{e}_{1}+\left(\mathrm{x}, \mathrm{e}_{2}\right) \mathrm{e}_{2}+\cdots+\left(\mathrm{x}, \mathrm{e}_{n}\right) \mathrm{e}_{n} \nonumber \]

In this equation, (x, \(e_k\))\(e_k\)(x,ek)ek is the component of \(x\) along \(e_k\), or the projection of \(x\) onto \(e_k\), but the set of unit coordinate vectors is not the only possible basis for decomposing a vector. Let's consider an arbitrary pair of orthogonal vectors \(x\) and \(y\):

\((\mathrm{x}, \mathrm{y})=0\).

The sum of \(x\) and \(y\) produces a new vector \(w\), illustrated in Figure 3, where we have used a two-dimensional drawing to represent \(n\) dimensions. The norm squared of \(w\) is

\[\begin{aligned}
\|\mathrm{w}\|^{2} &=(\mathrm{w}, \mathrm{w})=[(\mathrm{x}+\mathrm{y}),(\mathrm{x}+\mathrm{y})]=(\mathrm{x}, \mathrm{x})+(\mathrm{x}, \mathrm{y})+(\mathrm{y}, \mathrm{x})+(\mathrm{y}, \mathrm{y}) \\
&=\quad\|\mathrm{x}\|^{2}+\|\mathrm{y}\|^{2}
\end{aligned} \nonumber \]

This is the Pythagorean theorem in \(n\) dimensions! The length squared of \(w\) is just the sum of the squares of the lengths of its two orthogonal components.

Figure \(\PageIndex{3}\): Sum of Orthogonal Vectors

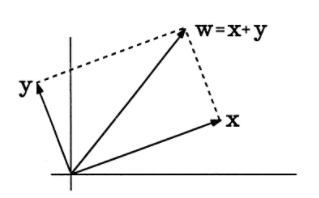
The projection of \(w\) onto \(x\) is \(x\), and the projection of \(w\) onto \(y\) is \(y\):

\(w=(1) x+(1) y\)

If we scale \(w\) by \(a\) to produce the vector z=\(a\)w, the orthogonal decomposition of \(z\) is

\(\mathrm{z}=a \mathrm{w}=(\mathrm{a}) \mathrm{x}+(\mathrm{a}) \mathrm{y}\).

Let's turn this argument around. Instead of building \(w\) from orthogonal vectors \(x\) and \(y\), let's begin with arbitrary \(w\) and \(x\) and see whether we can compute an orthogonal decomposition. The projection of \(w\) onto \(x\) is found from \(\mathrm{z}=\frac{\|\mathrm{x}\| \cos \theta}{\|\mathrm{y}\|} \mathrm{y}\).

\[w_{x}=\frac{(w, x)}{(x, x)} x \nonumber \]

But there must be another component of \(w\) such that \(w\) is equal to the sum of the components. Let's call the unknown component \(w_y\). Then

\[\mathrm{w}=\mathrm{w}_{\mathrm{x}}+\mathrm{w}_{\mathrm{y}} \nonumber \]

Now, since we know \(w\) and \(w_x\) already, we find \(w_y\) to be

\[\mathrm{w}_{\mathrm{y}}=\mathrm{w}-\mathrm{w}_{\mathrm{x}}=\mathrm{w}-\frac{(\mathrm{w}, \mathrm{x})}{(\mathrm{x}, \mathrm{x})} \mathrm{x} \nonumber \]

Interestingly, the way we have decomposed \(w\) will always produce \(w_x\) and \(w_{>y}\) orthogonal to each other. Let's check this:

\[\begin{array}{l}
\begin{aligned}
\left(\mathrm{w}_{\mathrm{x}}, \mathrm{w}_{\mathrm{y}}\right) &=\left(\frac{(\mathrm{w}, \mathrm{x})}{(\mathrm{x}, \mathrm{x})} \mathrm{x}, \mathrm{w}-\frac{(\mathrm{w}, \mathrm{x})}{(\mathrm{x}, \mathrm{x})} \mathrm{x}\right) \\
&=\frac{(\mathrm{w}, \mathrm{x})}{(\mathrm{x}, \mathrm{x})}(\mathrm{x}, \mathrm{w})-\frac{(\mathrm{w}, \mathrm{x})^{2}}{(\mathrm{x}, \mathrm{x})^{2}}(\mathrm{x}, \mathrm{x}) \\
&=\quad \frac{(\mathrm{w}, \mathrm{x})^{2}}{(\mathrm{x}, \mathrm{x})}-\frac{(\mathrm{w}, \mathrm{x})^{2}}{(\mathrm{x}, \mathrm{x})} \\
&= \qquad \qquad 0
\end{aligned}\\
\end{array} \nonumber \]

To summarize, we have taken two arbitrary vectors, \(w\) and \(x\), and decomposed \(w\) into a component in the direction of \(x\) and a component orthogonal to \(x\).