8.9: Graphics
- Page ID
- 10162
In "Complex Numbers", you learn that complex variables can be represented as points in the plane. MATLAB makes it easy for you to plot complex variables in a graph. Type z1 = 1+.5*j;plot(z1,'o'). The graph window should be activated and the point z1 displayed by a 'o'. You must specify the symbol for display, and the authorized symbols for point display are '.', 'o', '+', and '*'. When you are displaying a curve (to come later), no type is necessary. MATLAB automatically adjusts the scale on a graph to accommodate the value of the point being plotted. In this case, the range is [0,2] for the real part and [0,1] for the imaginary part.
Let's now plot a second complex number by typing z2 = 2+1.5*j; plot(za,'o'). Note that the second plot command erases the first plot and changes the scaling to [0,4] and [0,3]. Sometimes you may want to have the points plotted on the same graph. To achieve this, you have to use the command hold on after the first plot. Try the following:
≫ plot(z2,'o') ≫ hold on ≫ plot(z1,'o') ≫ hold off
The advantage in using the hold command is that there is no limit to the number of plot commands you can type before the hold is turned off, and these plots may involve the same variable plotted over a range of values. You can also use different point displays. A disadvantage of the hold command is that the scaling is enforced by the first plot and is not adjusted for subsequent plots. This is why we plot the point z2 first. Try reversing the order of the plots and see what happens. This means that points outside the scaling will not be displayed. The command hold off permits erasing the current graph for the next plot command.
You can freeze the scaling of the graph by using the command axis. MATLAB gives you the message
Axis scales frozen ans = 0 4 0 3
This freezes the current axis scaling for subsequent plots. Similarly, if you type axis a second time, MATLAB resumes the automatic scaling feature and prints the message
Axis scales auto-ranged ans = 0 4 0 3
The axis scaling can also be manually enforced by using the command
≫ axis([xmin xmax ymin ymax])
where (xmin, ymin) is the lower left corner and (xmax, ymax) is the upper right corner of the graph. This scaling remains in effect until the next axis command is entered (with or without arguments).
Another way to plot several complex numbers on the same graph is to display them as a curve. For this purpose, you have to store the numbers in a vector. For example, type z1 = z1,z(2) = z2,plot(z). Note that the two points are at the two extremes of the line plotted on the graph. If you specify a symbol, then no line is drawn, just the extreme points. Try plot(z,'o') .
If you examine your current graph carefully, you will notice that the unit lengths on the x and y axes are not quite the same. In fact, MATLAB adjusts the length of an axis to conform to the overall size of the graph window. What this means is that a 45\(^{\circ}\) line will actually be displayed at an angle depending on the overall aspect ratio of the graph window. To ensure that the aspect ratio is equal to 1, you may enter the command axis('square'). MATLAB will then enforce an aspect ratio equal to 1, regardless of the aspect ratio for the outside graph window. This ensures that circles appear as circles and not as ellipses. MATLAB will make the square graph as large as possible to fit within the graph window. To go back to the default ratio, just type in axis('normal').
To add labels to your graph, the functions xlabel('text'), ylabel('text'), and title('text') are useful and self-explanatory. The argument text contains a string of characters. Add the label Real on the horizontal axis and the label Imaginary on the vertical axis of your graph. The command grid draws a grid on your graph. The grid does not remain in effect for the next plots. Try it.
The plot Instruction
The plot instruction in MATLAB is very versatile. It can be used to plot several different types of data. Its syntax is plot(x,y,' symbol and/or color') or plot(y,'symbol and/or color'). The instruction will plot a vector of data versus another vector of data. The first vector is referenced to the horizontal axis and the second to the vertical axis. If only one vector is used, then it is plotted with reference to the vertical axis while the horizontal axis is automatically forced to be the index of the vector for the corresponding data point. The notation inside the apostrophes is optionally used to designate whether each element of the vector is to be plotted as a single point with a certain symbol or as a curve with a straight line drawn between each data value. The colors can also be specified. Possible symbols are (*,o,+,.), and colors are (r,g,b,w) (red, green, blue, and white). Complex valued vectors are plotted by making the horizontal axis the real part of the vector and the vertical axis the imaginary part. Warning: A complex valued vector will automatically be plotted correctly on the complex plane (instead of real versus imaginary) only if every element of the vector is complex valued. Try plot (x,y,'*') , plot (x,'*'), plot (y,'*'), plot (y,x,'*') and plot (z,'*'), plot (Real (z), Imag (z),'*') to clarify your understanding of plot. Use \(\mathrm{x}=[1357], \mathrm{y}=[2468]\), \(z = [1+j, 2+2 j, 3+3 j]\).
We may summarize as follows:
plot(x,'*r') |
(red star—points with the values of x on vertical and indicies on horizontal) |
plot(y) |
(line—connected curve of the value of y on vertical and the value of x on horizontal) |
plot(x,y,'og') |
(line—connected curve of the value of y on vertical and the value of x on horizontal) |
plot(x,y,'og') |
(circle—points of the value of y on vertical and the value of x on horizontal) |
plot(real(z),imag(z)) |
(line—connectedplot of z on the complex plane) |
plot(real(z),imag(z),'+b') |
(blue plus—points of z on the complex plane). |
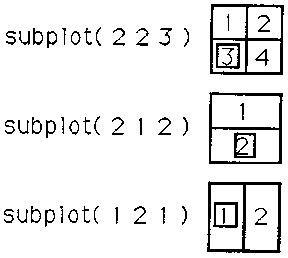
Subplots
It is possible to split the graphics screen up into several separate smaller graphs rather than just one large graph. As many as four subplots can be created. The MATLAB instruction subplot (mnp) signifies which of the smaller graphs is to be accessed with the next plot statement. The mnp argument consists of three digits. The m and n are the numbers of rows (m) and columns (n) into which the screen should be divided. The p designates which of the matrix elements is to be used. For example,
Help and Demos
MATLAB has on-line help and a collection of demonstrations. For a list of available functions, type
≫ help
For help on a specific function, sin for example, type
≫ help sin
To learn how to use colon (;, a very important and versatile character) in MATLAB, type
≫ help :
The demos will also help you become more familiar with MATLAB and its capabilities. To run them, type
≫ demo


