2.6: Simple Systems
- Page ID
- 1604
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Systems manipulate signals.
- There are a few simple systems which will perform simple functions upon signals. Examples include amplification (or attenuation), time-reversal, delay, and differentiation/integration.
Systems manipulate signals, creating output signals derived from their inputs. Why the following are categorized as "simple" will only become evident towards the end of the course.
Sources
Sources produce signals without having input. We like to think of these as having controllable parameters, like amplitude and frequency. Examples would be oscillators that produce periodic signals like sinusoids and square waves and noise generators that yield signals with erratic waveforms (more about noise subsequently). Simply writing an expression for the signals they produce specifies sources. A sine wave generator might be specified by:
\[y(t) = A\sin (2\pi f_{0}t)u(t) \nonumber \]
The above equation says that the source was turned on at t =0 to produce a sinusoid of amplitude A and frequency f0.
Amplifiers
An amplifier multiplies its input by a constant known as the amplifier gain.
\[y(t) = Gx(t) \nonumber \]
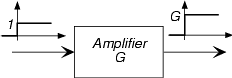
The gain can be positive or negative (if negative, we would say that the amplifier inverts its input) and its magnitude can be greater than one or less than one. If less than one, the amplifier actually attenuates. A real-world example of an amplifier is your home stereo. You control the gain by turning the volume control.
Delay
A system serves as a time delay when the output signal equals the input signal at an earlier time.
\[y(t) = x(t-\tau ) \nonumber \]
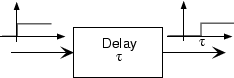
Here, τ is the delay. The way to understand this system is to focus on the time origin: The output at time t = τ equals the input at time t = 0 Thus, if the delay is positive, the output emerges later than the input, and plotting the output amounts to shifting the input plot to the right. The delay can be negative, in which case we say the system advances its input. Such systems are difficult to build (they would have to produce signal values derived from what the input will be), but we will have occasion to advance signals in time.
Time Reversal
Here, the output signal equals the input signal flipped about the time origin.
\[y(t) = x(-t) \nonumber \]
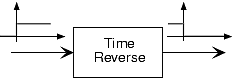
Again, such systems are difficult to build, but the notion of time reversal occurs frequently in communications systems.
Mentioned earlier was the issue of whether the ordering of systems mattered. In other words, if we have two systems in cascade, does the output depend on which comes first? Determine if the ordering matters for the cascade of an amplifier and a delay and for the cascade of a time-reversal system and a delay.
Solution
In the first case, order does not matter; in the second it does. "Delay" means t → t - τ. "Time-reverse" means t → -t.
Case 1
\[y(t) = Gx(t-\tau ) \nonumber \]
The way we apply the gain and delay the signal gives the same result.
Case 2
- Time-reverse then delay:
\[y(t) = x\left ( - (t-\tau )\right ) = x(-t+\tau ) \nonumber \]
- Delay then time-reverse:
\[y(t) = x\left ( (-t)-\tau )\right ) \nonumber \]
Derivative Systems and Integrators
Systems that perform calculus-like operations on their inputs can produce waveforms significantly different than present in the input. Derivative systems operate in a straightforward way: A first-derivative system would have the input-output relationship
\[y(t) = \frac{\mathrm{d} }{\mathrm{d} t}x(t) \nonumber \]
Integral systems have the complication that the integral's limits must be defined. It is a signal theory convention that the elementary integral operation have a lower limit of \(-\infty \nonumber \) and that the value of all signals at \(t = -\infty \nonumber \) equals zero. A simple integrator would have input-output relation:
\[y(t) = \int_{-\infty }^{t}x(\alpha )d\alpha \nonumber \]
Linear Systems
Linear systems are a class of systems rather than having a specific input-output relation. Linear systems form the foundation of system theory, and are the most important class of systems in communications. They have the property that when the input is expressed as a weighted sum of component signals, the output equals the same weighted sum of the outputs produced by each component. When S(•) is linear,
\[S\left ( G_{1}x_{1}(t)+ G_{2}x_{2}(t) \right ) = G_{1}S(x_{1}(t))+ G_{2}S(x_{2}(t)) \nonumber \]
for all choices of signals and gains.
This general input-output relation property can be manipulated to indicate specific properties shared by all linear systems.
\[S(Gx(t)) = GS(x(t)) \nonumber \]
The colloquialism summarizing this property is "Double the input, you double the output." Note that this property is consistent with alternate ways of expressing gain changes: Since 2x(t) also equals x(t)+x(t), the linear system definition provides the same output no matter which of these is used to express a given signal.
\[S(0) = 0 \nonumber \]
If the input is identically zero for all time, the output of a linear system must be zero. This property follows from the simple derivation:
\[S(0) = S(x(t)-x(t)) = S(x(t)) - S(x(t)) = 0 \nonumber \]
Just why linear systems are so important is related not only to their properties, which are divulged throughout this course, but also because they lend themselves to relatively simple mathematical analysis. Said another way, "They're the only systems we thoroughly understand!"
We can find the output of any linear system to a complicated input by decomposing the input into simple signals. The equation above says that when a system is linear, its output to a decomposed input is the sum of outputs to each input. for example if,
\[x(t) = e^{-t} + \sin (2\pi f_{0}t) \nonumber \]
The output S(x(t)) of any linear system equals
\[y(t) = S(e^{-t}) + S(\sin (2\pi f_{0}t)) \nonumber \]
Time-Invariant Systems
Systems that don't change their input-output relation with time are said to be time-invariant. The mathematical way of stating this property is to use the signal delay concept described in Simple Systems above.
\[(y(t) = S(x(t))) \Rightarrow (y(t-\tau ) = S(x(t-\tau ))) \nonumber \]
If you delay (or advance) the input, the output is similarly delayed (advanced). Thus, a time-invariant system responds to an input you may supply tomorrow the same way it responds to the same input applied today; today's output is merely delayed to occur tomorrow.
The collection of linear, time-invariant systems are the most thoroughly understood systems. Much of the signal processing and system theory discussed here concentrates on such systems. For example, electric circuits are, for the most part, linear and time-invariant. Nonlinear ones abound, but characterizing them so that you can predict their behavior for any input remains an unsolved problem.