5.8: Properties of Information

Last updated
Save as PDF

Page ID: 50963

Paul Penfield, Jr.
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

It is convenient to think of physical quantities as having dimensions. For example, the dimensions of velocity are length over time, and so velocity is expressed in meters per second. In a similar way it is convenient to think of information as a physical quantity with dimensions. Perhaps this is a little less natural, because probabilities are inherently dimensionless. However, note that the formula uses logarithms to the base 2. The choice of base amounts to a scale factor for information. In principle any base \(k\) could be used, and related to our definition by the identity

\(\log_k(x) = \dfrac{\log_2(x)}{\log_2(k)} \tag{5.15}\)

With base-2 logarithms the information is expressed in bits. Later, we will find natural logarithms to be useful.

If there are two events in the partition with probabilities \(p\) and \((1 − p)\), the information per symbol is

\(I = p\log_2\Big(\dfrac{1}{p}\Big) + (1-p)\log_2\Big(\dfrac{1}{1-p}\Big)\tag{5.16}\)

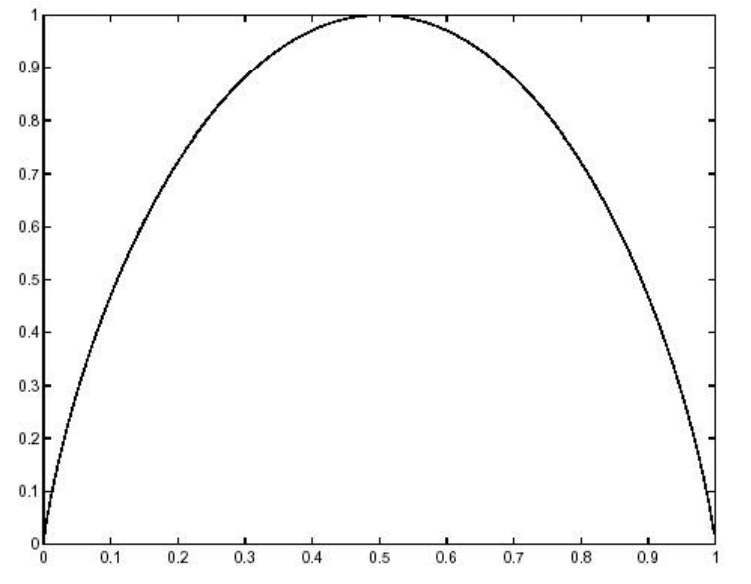
which is shown, as a function of \(p\), in Figure 5.3. It is largest (1 bit) for \(p\) = 0.5. Thus the information is a maximum when the probabilities of the two possible events are equal. Furthermore, for the entire range of probabilities between \(p\) = 0.4 and \(p\) = 0.6 the information is close to 1 bit. It is equal to 0 for \(p\) = 0 and for \(p\) = 1. This is reasonable because for such values of \(p\) the outcome is certain, so no information is gained by learning it.

For partitions with more than two possible events the information per symbol can be higher. If there are \(n\) possible events the information per symbol lies between 0 and \(\log_2(n)\) bits, the maximum value being achieved when all probabilities are equal.

Screen Shot 2021-05-04 at 12.30.00 AM.png — Figure 5.3: Entropy of a source with two symbols as a function of \(p\), one of the two probabilities