Skip to main content
Engineering LibreTexts

5.10: Detail- Life Insurance

  1. Last updated
  2. Save as PDF
  • Page ID
    50965

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    An example of statistics and probability in everyday life is their use in life insurance. We consider here only one-year term insurance (insurance companies are very creative in marketing more complex policies that combine aspects of insurance, savings, investment, retirement income, and tax minimization).

    When you take out a life insurance policy, you pay a premium of so many dollars and, if you die during the year, your beneficiaries are paid a much larger amount. Life insurance can be thought of in many ways.

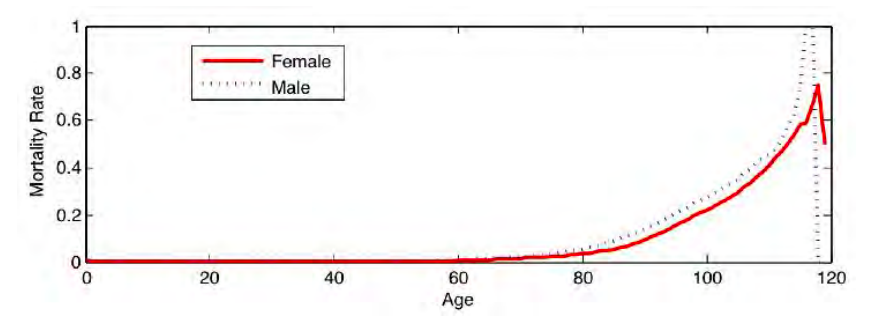
    From a gambler’s perspective, you are betting that you will die and the insurance company is betting that you will live. Each of you can estimate the probability that you will die, and because probabilities are subjective, they may differ enough to make such a bet seem favorable to both parties (for example, suppose you know about a threatening medical situation and do not disclose it to the insurance company). Insurance companies use mortality tables such as Table 5.2 (shown also in Figure 5.4) for setting their rates. (Interestingly, insurance companies also sell annuities, which from a gambler’s perspective are bets the other way around—the company is betting that you will die soon, and you are betting that you will live a long time.)

    Another way of thinking about life insurance is as a financial investment. Since insurance companies on average pay out less than they collect (otherwise they would go bankrupt), investors would normally do better investing their money in another way, for example by putting it in a bank.

    Most people who buy life insurance, of course, do not regard it as either a bet or an investment, but rather as a safety net. They know that if they die, their income will cease and they want to provide a partial replacement for their dependents, usually children and spouses. The premium is small because the probability of death is low during the years when such a safety net is important, but the benefit in the unlikely case of death may be very important to the beneficiaries. Such a safety net may not be as important to very rich people (who can afford the loss of income), single people without dependents, or older people whose children have grown up.

    Figure 5.4 and Table 5.2 show the probability of death during one year, as a function of age, for the cohort of U. S. residents born in 1988 (data from The Berkeley Mortality Database\(^2\)).

    Screen Shot 2021-05-04 at 10.00.17 PM.png
    Figure 5.4: Probability of death during one year for U. S. residents born in 1988.
    Age Female Male Age Female Male Age Female Male

    0

    		 0.008969 0.011126 40 0.000945 0.002205 80 0.035107 0.055995
    1 0.000727 0.000809 41 0.001007 0.002305 81 0.038323 0.061479
    2 0.000384 0.000526 42 0.00107 0.002395 82 0.041973 0.067728
    3 0.000323 0.000415 43 0.001144 0.002465 83 0.046087 0.074872
    4 0.000222 0.000304 44 0.001238 0.002524 84 0.050745 0.082817
    5 0.000212 0.000274 45 0.001343 0.002605 85 0.056048 0.091428
    6 0.000182 0.000253 46 0.001469 0.002709 86 0.062068 0.100533
    7 0.000162 0.000233 47 0.001616 0.002856 87 0.06888 0.110117
    8 0.000172 0.000213 48 0.001785 0.003047 88 0.076551 0.120177
    9 0.000152 0.000162 49 0.001975 0.003295 89 0.085096 0.130677
    10 0.000142 0.000132 50 0.002198 0.003566 90 0.094583 0.141746
    11 0.000142 0.000132 51 0.002454 0.003895 91 0.105042 0.153466
    12 0.000162 0.000203 52 0.002743 0.004239 92 0.116464 0.165847
    13 0.000202 0.000355 53 0.003055 0.00463 93 0.128961 0.179017
    14 0.000263 0.000559 54 0.003402 0.00505 94 0.142521 0.193042
    15 0.000324 0.000793 55 0.003795 0.005553 95 0.156269 0.207063
    16 0.000395 0.001007 56 0.004245 0.006132 96 0.169964 0.221088
    17 0.000426 0.001161 57 0.004701 0.006733 97 0.183378 0.234885
    18 0.000436 0.001254 58 0.005153 0.007357 98 0.196114 0.248308
    19 0.000426 0.001276 59 0.005644 0.008028 99 0.208034 0.261145
    20 0.000406 0.001288 60 0.006133 0.008728 100 0.220629 0.274626
    21 0.000386 0.00131 61 0.006706 0.009549 101 0.234167 0.289075
    22 0.000386 0.001312 62 0.007479 0.010629 102 0.248567 0.304011
    23 0.000396 0.001293 63 0.008491 0.012065 103 0.263996 0.319538
    24 0.000417 0.001274 64 0.009686 0.013769 104 0.280461 0.337802
    25 0.000447 0.001245 65 0.011028 0.015702 105 0.298313 0.354839
    26 0.000468 0.001226 66 0.012368 0.017649 106 0.317585 0.375342
    27 0.000488 0.001237 67 0.013559 0.019403 107 0.337284 0.395161
    28 0.000519 0.001301 68 0.014525 0.020813 108 0.359638 0.420732
    29 0.00055 0.001406 69 0.015363 0.022053 109 0.383459 0.439252
    30 0.000581 0.001532 70 0.016237 0.023393 110 0.408964 0.455882
    31 0.000612 0.001649 71 0.017299 0.025054 111 0.437768 0.47619
    32 0.000643 0.001735 72 0.018526 0.027029 112 0.466216 0.52
    33 0.000674 0.00179 73 0.019972 0.029387 113 0.494505 0.571429
    34 0.000705 0.001824 74 0.02163 0.032149 114 0.537037 0.625
    35 0.000747 0.001859 75 0.023551 0.035267 115 0.580645 0.75
    36 0.000788 0.001904 76 0.02564 0.038735 116 0.588235 1
    37 0.00083 0.001961 77 0.027809 0.042502 117 0.666667 1
    38 0.000861 0.002028 78 0.030011 0.046592 118 0.75 0
    39 0.000903 0.002105 79 0.032378 0.051093 119 0.5 0
    Table 5.2: Mortality table for U. S. residents born in 1988

    \(^2\)The Berkeley Mortality Database can be accessed online: http://www.demog.berkeley.edu/ bmd/states.html

    This page titled 5.10: Detail- Life Insurance is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Paul Penfield, Jr. (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.