4.2: Response of a First Order System to a Suddenly Applied Cosine
- Page ID
- 7643
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)First, we derive a complete solution in the conventional manner for the original standard 1st order ODE \(\dot{x}-a x=b u(t)\) [Equation 1.2.1], with IC \(x(0)=x_{0}\), and with the suddenly applied (at \(t\) = 0) cosine input \(u(t)=U \cos \omega t\), \(t\) > 0, where \(U\) is a constant amplitude [Problem 2.12.2].
\[\mathrm{ODE}+\mathrm{IC}: \dot{x}-a x=b U \cos \omega t=b U \frac{e^{j \omega t}+e^{-j \omega t}}{2}, x(0)=x_{0}, \text { find } x(t) \text { for } t>0\label{eqn:4.1} \]
Laplace transformation of ODE + IC: \(s X(s)-x_{0}-a X(s)=\frac{b U}{2}\left(\frac{1}{s-j \omega}+\frac{1}{s+j \omega}\right)\)
Solve for \(X(s)\):
\[X(s)=\frac{x_{0}}{s-a}+\frac{b U}{2} \frac{1}{(s-a)}\left(\frac{1}{s-j \omega}+\frac{1}{s+j \omega}\right) \nonumber \]
Completed partial-fraction expansion (Problem 2.8):
\[X(s)=\frac{x_{0}}{s-a}+\frac{b U}{2} \frac{1}{a^{2}+\omega^{2}}\left(\frac{2 a}{s-a}+\frac{-a-j \omega}{s-j \omega}+\frac{-a+j \omega}{s+j \omega}\right) \nonumber \]
Inverse transform:
\[ \begin{align} x(t) &=x_{0} e^{a t}+\frac{b U}{a^{2}+\omega^{2}}\left[a e^{a t}+\frac{1}{2}\left((-a-j \omega) e^{j \omega t}+(-a+j \omega) e^{-j \omega t}\right)\right] \\[4pt] \quad x(t)&=x_{0} e^{a t}+\frac{b U}{a^{2}+\omega^{2}}\left[a e^{a t}+\frac{1}{2}\left((-a)\left(e^{j \omega t}+e^{-j \omega t}\right)+\omega \frac{e^{j \omega t}-e^{-j \omega t}}{j}\right)\right] \\[4pt] x(t)&=x_{0} e^{a t}+\frac{b U}{a^{2}+\omega^{2}}\left(a e^{a t}-a \cos \omega t+\omega \sin \omega t\right), t \geq 0 \\[4pt] x(t) &= x_{0} e^{a t}+\left(\frac{b}{-a}\right) \frac{U}{\left[1+\left(\frac{\omega}{-a}\right)^{2}\right]}\left[-e^{a t}+\cos \omega t+\left(\frac{\omega}{-a}\right) \sin \omega t\right], t \geq 0\label{eqn:4.2} \end{align} \]
Next, we adapt solution Equation \(\ref{eqn:4.2}\) of general 1st order problem Equation \(\ref{eqn:4.1}\) to the damper-spring system (ideal shock strut) of Figure 3.7.1 with suddenly applied cosine force input \(f_{x}(t)=F \cos \omega t\), for which the comparable ODE + IC problem is
\[c \dot{x}+k x=F \cos \omega t, x(0)=x_{0}, \text { find position } x(t) \text { for } t>0\label{eqn:4.3} \]
Comparing Equation \(\ref{eqn:4.3}\) with Equation \(\ref{eqn:4.1}\), we define \(U\) \(\equiv\) \(F\), then the other constants of the standard equation become
\[a=-\frac{k}{c} \equiv-\frac{1}{\tau_{1}} \Rightarrow \text { time constant } \tau_{1} \equiv \frac{1}{-a}=\frac{c}{k} \quad \text { and } \quad b=\frac{1}{c} \text { and } \frac{b}{-a}=\frac{1}{k} \nonumber \]
\[\Rightarrow \quad x(t)=x_{0} e^{-t / \tau_{1}}+\frac{F}{k}\left(\frac{1}{1+\left(\omega \tau_{1}\right)^{2}}\right)\left(-e^{-t / \tau_{1}}+\cos \omega t+\omega \tau_{1} \sin \omega t\right), t \geq 0\label{eqn:4.4} \]
It is instructive to study the physical nature of response Equation \(\ref{eqn:4.4}\) in the context of a specific numerical example. Consider an ideal shock strut with the initial condition \(x_0\) = -2 m, and with the system parameters \(c=1 / \pi\) N/(m/s) = 0.3183 N-s/m and \(k\) = 1 N/m, so that time constant \(\tau_{1}=1 / \pi\) s = 0.3183 s. Let the magnitude of the cosine force be \(F\) = 1.5 N, and let the period of the cosine be \(T_p\) = 1 s/cycle. Therefore, the cyclic frequency is \(f\) = 1 Hz (cycle/s), and the circular frequency is \(\omega = 2\pi\) radians/s. (Period, frequency, and phase of periodic signals are discussed more generally in Section 4.4.) The numerical solution of Equation \(\ref{eqn:4.4}\) with these parameters for time 0 \(\leq\) \(t\) \(\leq\) 3 s is calculated and graphed in the following MATLAB operations.
MATLAB M-file script:
%MATLABdemo41.m
%Damper-spring ideal shock strut response to IC + cosine forcing
c=1/pi;k=1; %system viscous damping & stiffness constants, SI units
F=1.5;Tp=1; %cosine forcing: amplitude (N), period (sec)
xo=-2; %initial displacement (m)
w=2*pi/Tp; %circular frequency of cosine forcing (rad/sec)
t1=c/k;denom=1+(w*t1)^2;
t=0:0.01:3*Tp; %time instants for forced response
fx=F*cos(w*t);
x=(xo-(F/k)/denom)*exp(-t/t1)+(F/k)/denom*(cos(w*t)+w*t1*sin(w*t));
plot(t,fx,'k',t,x,'k.'),grid,xlabel('Time t (sec)'),... ylabel('Force input f_x(t) (N) and displacement output x(t) (m)'),... title('Time response of an ideal shock strut to IC + cosine input')
MATLAB command/responses:
>> MATLABdemo41
The graph of input \(f_x(t)\) and response \(x(t)\) is below (after figure editing in MATLAB,Version 6 or later, to flatten the aspect ratio and to distinguish the two curves).
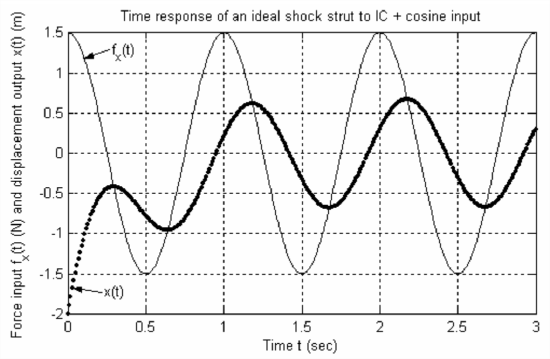
Let us observe from the graph some important features of the response:
- As calculated above, the time constant of the exponential decay terms in Equation \(\ref{eqn:4.4}\) [the two terms involving \(\exp \left(-t / \tau_{1}\right)\)] is \(\tau_{1}\) = 0.3183 s, so the settling time for those terms is \(4 \tau_{1}\) = 1.273 s. In other words, the exponential decay terms in \(x(t)\) have essentially vanished after about 1.3 s of response, and this is clear from the graph. Because the exponential decay terms are relatively short-lived, we often refer to them as the “transient” part of the total solution.
- After the exponential decay terms have vanished, only the \(\cos \omega t\) and \(\sin \omega t\) terms of Equation \(\ref{eqn:4.4}\) remain. It appears from the graph that those two terms combine to make a single sinusoid at frequency \(\omega\), and that the remaining steady-state \(x(t)\) sinusoid is displaced in time by a constant time lag from the \(F_x(t)\) sinusoid. This steady-state sinusoidal response is what we call the frequency response, and we will derive equations that describe it explicitly in the remainder of the chapter.


