15.1: Initial Definitions and PID Control
- Page ID
- 7719
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Figure \(\PageIndex{1}\) is a general functional block diagram that represents many engineering control systems. The term input-error operation can be defined in the context of this diagram: a single output quantity is fed back and differenced from the operator-setting input quantity, and the error signal is manipulated mathematically by a controller, also called control processor or filter, in such a way as to produce effective control. The controller usually consists of analog electronic circuitry and/or a digital processor.
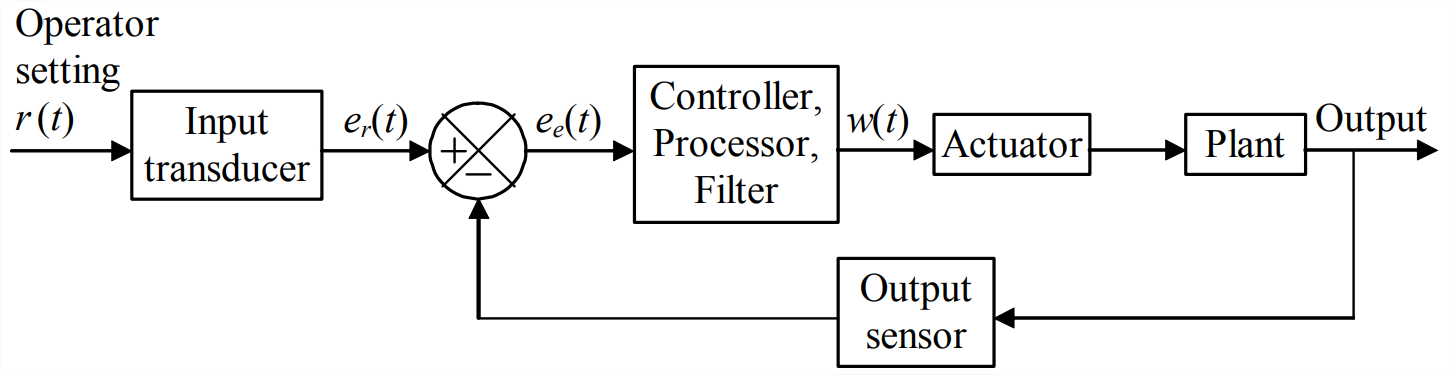
Proportional-integral-derivative (PID) control is a class of input-error operations used widely in industry. Let \(e_{e}(t)\) be the error voltage signal that is input to the controller and \(w(t)\) be the output voltage from the controller, as shown on Figure \(\PageIndex{1}\). The mathematical operations performed by an ideal PID controller are described by the equation
\[w(t)=P\left[e_{e}(t)+b_{i} \frac{1}{\tau_{i}} \int_{t=0}^{\tau=t} e_{e}(\tau) d \tau+b_{d} \tau_{d} \frac{d e_{e}}{d t}(t)\right]\label{eqn:15.1} \]
The physical constants in Equation \(\ref{eqn:15.1}\) are proportional gain \(P\), integral time constant \(\tau_{i}\), and derivative time constant \(\tau_{d}\). Each of the binary constants \(b_{i}\) and \(b_{d}\) has dimensionless value 1 or 0, depending upon whether or not integral and/or derivative actions are included in the control. Determining what these constants should be for a particular application is a major part of the control design process. To find the transfer function of the ideal PID controller, we define the Laplace transforms \(L\left[e_{e}(t)\right] \equiv E_{e}(s)\) and \(L[w(t)] \equiv W(s)\). Taking the Laplace transform of Equation \(\ref{eqn:15.1}\) gives the ideal-PID-controller transfer function:
\[\frac{W(s)}{E_{e}(s)}=P\left[1+b_{i} \frac{1}{\tau_{i} s}+b_{d} \tau_{d} s\right]\label{eqn:15.2} \]
We shall consider in examples three subsets of PID control that are in common usage: for proportional (P) control, only the first term inside the brackets of Equations \(\ref{eqn:15.1}\) and \(\ref{eqn:15.2}\) is used, so \(b_{i}=b_{d}=0\); for proportional-integral (PI) control, only the first and second terms are used, so \(b_{i}=1\) and \(b_{d}=0\); and for proportional-derivative (PD) control, only the first and third terms are used, so \(b_{i}=0\) and \(b_{d}=1\).
To make the concept of PI control, for example, more concrete, Figure \(\PageIndex{2}\) depicts a specific analog electrical circuit that, in principle, acts as an ideal PI controller. (In practice, a great deal of electronic refinement and conditioning is required to produce a circuit that behaves even close to ideally.) By applying the methods of circuit analysis described in Chapter 5 (homework Problem 5.11), we can show that the PI (\(b_{i}=1\) and \(b_{d}=0\)) constants in Equations \(\ref{eqn:15.1}\) and \(\ref{eqn:15.2}\), expressed in terms of the circuit parameters of Figure \(\PageIndex{2}\), are:
\[P=\frac{R_{3} C_{1}}{R_{2} C_{2}}, \quad \tau_{i}=R_{1} C_{1}\label{eqn:15.3} \]
The detailed design of PID controllers involves a great deal of engineering art as well as engineering science, and it has been developed extensively; see, e.g., Ogata, 2001, Chapter 10. The present chapter is just an introduction to PID control, so we will not delve deeply into design details; instead, we shall explore some of the more general characteristics of P, PI, and PD types of control in the context of relatively simple examples.