3.6: BIBO Stability of Continuous Time Systems

Last updated
Save as PDF

Page ID: 22856

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Introduction

BIBO stability stands for bounded input, bounded output stability. BIBO stablity is the system property that any bounded input yields a bounded output. This is to say that as long as we input a signal with absolute value less than some constant, we are guaranteed to have an output with absolute value less than some other constant.

Continuous Time BIBO Stability

In order to understand this concept, we must first look more closely into exactly what we mean by bounded. A bounded signal is any signal such that there exists a value such that the absolute value of the signal is never greater than some value. Since this value is arbitrary, what we mean is that at no point can the signal tend to infinity, including the end behavior.

Figure \(\PageIndex{1}\): A bounded signal is a signal for which there exists a constant \(A\) such that \(\forall t:(|f(t)|<A)\)

Time Domain Conditions

Now that we have identified what it means for a signal to be bounded, we must turn our attention to the condition a system must possess in order to guarantee that if any bounded signal is passed through the system, a bounded signal will arise on the output. It turns out that a continuous time LTI (Section 2.1) system with impulse response \(h(t)\) is BIBO stable if and only if

Continuous-Time Condition for BIBO Stability

\[\int_{-\infty}^{\infty}|h(t)| \mathrm{d} t<\infty \nonumber \]

This is to say that the impulse response is absolutely integrable.

Laplace Domain Conditions

Stability is very easy to infer from the pole-zero plot of a transfer function. The only condition necessary to demonstrate stability is to show that the \(i\omega\)-axis is in the region of convergence. Consequently, for stable causal systems, all poles must be to the left of the imaginary axis.

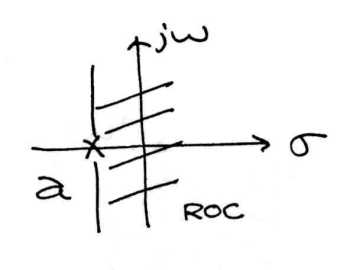Figure \(\PageIndex{2}\): (a) Example of a pole-zero plot for a stable continuous-time system. (b) Example of a pole-zero plot for an unstable continuous-time system.

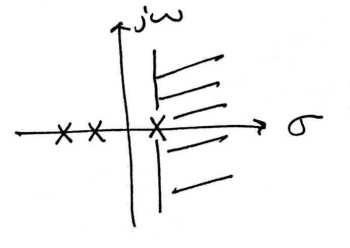BIBO Stability Summary

Bounded input bounded output stability, also known as BIBO stability, is an important and generally desirable system characteristic. A system is BIBO stable if every bounded input signal results in a bounded output signal, where boundedness is the property that the absolute value of a signal does not exceed some finite constant. In terms of time domain features, a continuous time system is BIBO stable if and only if its impulse response is absolutely integrable. Equivalently, in terms of Laplace domain features, a continuous time system is BIBO stable if and only if the region of convergence of the transfer function includes the imaginary axis.