6.4: Regional Transmission Organizations

Regional Transmission Organizations

Regional Transmission Organizations (RTOs) are non-profit, public-benefit corporations that were created as a part of electricity restructuring in the United States, beginning in the 1990s. Some RTOs, such as PJM in the Mid-Atlantic states, were created from existing “power pools” dating back many decades (PJM was first organized in the 1920s). The history of the RTO dates back to FERC Orders 888 and 889, which suggested the concept of the “Independent System Operator” (ISO) to ensure non-discriminatory access to transmission systems. FERC Order 2000 encouraged, but did not quite require, all transmission-owning entities to form or join a Regional Transmission Organization to promote the regional administration of high-voltage transmission systems. The difference between RTO and ISO is, at this point, largely semantic. Order 2000 contains a set of technical requirements for any system operator to be considered a FERC-approved RTO.

RTOs are regulated by FERC, not by the states (i.e., RTO rules are determined by a FERC-approved tariff and not by state Public Utility Commissions) and membership in a RTO by any entity is voluntary. Including Texas (which is technically outside of FERC’s jurisdiction), there are seven RTOs in the U.S., covering about half of the states and roughly two-thirds of total U.S. annual electricity demand. Each RTO establishes its own rules and market structures, but there are many commonalities. Broadly, the RTO performs the following functions:

1. management of the bulk power transmission system within its footprint;
2. ensuring non-discriminatory access to the transmission grid by customers and suppliers;
3. dispatch of generation assets within its footprint to keep supply and demand in balance;
4. regional planning for generation and transmission (though see below for limitations to this function);
5. with the exception of the Southwest Power Pool (SPP), RTOs also run a number of markets for electric generation service.

In many ways, RTOs perform the same functions as the vertically-integrated utilities that were supplanted by electricity restructuring. There are, however, a number of important distinctions between RTOs and utilities.

1. RTOs do not sell electricity to retail customers. RTOs purchase power from generators, resell it to electric distribution utilities, who then resell it again to end-use customers.
2. RTOs may not earn profits.
3. RTOs do not own any physical assets – they do not own generators, power lines or any other equipment. RTOs generally cannot force generation or transmission companies to make investments.
4. RTO decision-making is governed by a “stakeholder board” consisting of various electric sector constituencies. In some cases, the RTO can implement policy unilaterally without approval by the stakeholder board, but this is generally rare. All policies must, however, be approved by FERC.
5. RTOs do not take any financial or physical position in the markets they operate. They must remain neutral market-makers, although they do monitor activity in their markets to avoid manipulation by individual generators or groups of generators.

The set of NETL power market primers zipped file contains more information on specific differences between the various RTO markets.

The separation of ownership from control in RTO markets raises some interesting complications for planning. RTOs have responsibility for ensuring reliability and adequacy of the power grid. They must perform regional planning, meaning that they determine where additional power lines and generators are required in order to maintain system reliability. But RTOs generally cannot require that member companies make any investments. They generally rely on a variety of market mechanisms to create financial incentives for member firms to invest in generation. Many transmission investments needed for reliability are eligible for fixed rates of return set by FERC.

Operating a power system requires making decisions on time scales covering fifteen orders of magnitude prior to real-time dispatch, as shown in \(Figure \text { } 6.5\).

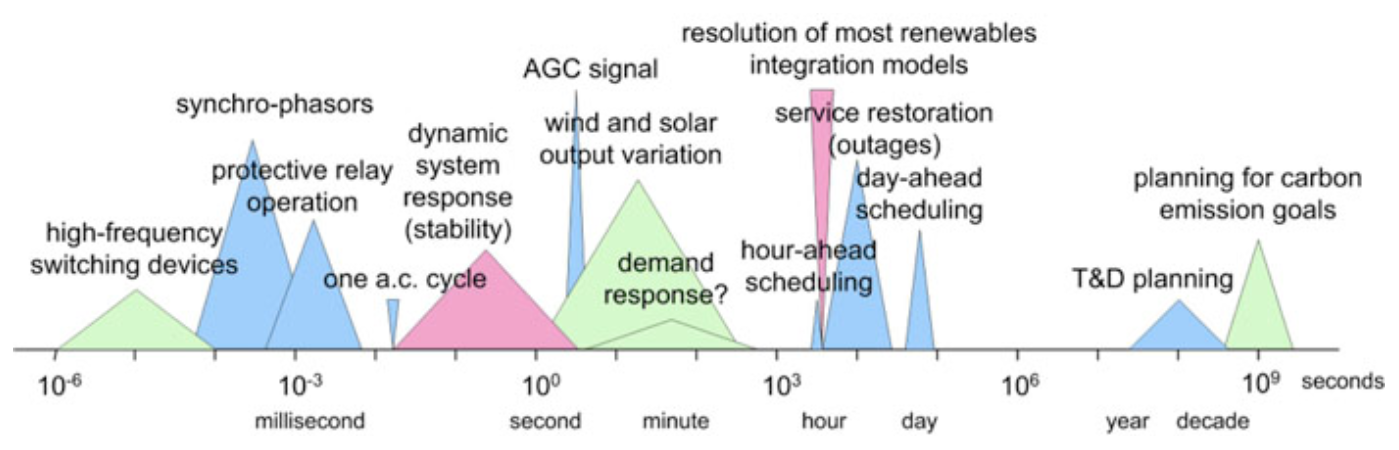
\(Figure \text { } 6.5\): Schematic of time scales involved in power system planning and operations.

Since the RTO does not own any physical assets, it must effectively sign contracts with generation suppliers to provide needed services. The market mechanisms run by the RTO are used to procure generation supplies needed to maintain reliability. Once generation supplies are procured by the RTO, it can dispatch generation as needed to meet demand.

RTOs run three types of markets that enable them to manage the power grid over time scales ranging from cycles (one cycle = 1/60^th of one second) to several years in advance of real-time dispatch, as shown in \(Figure 6.6\).

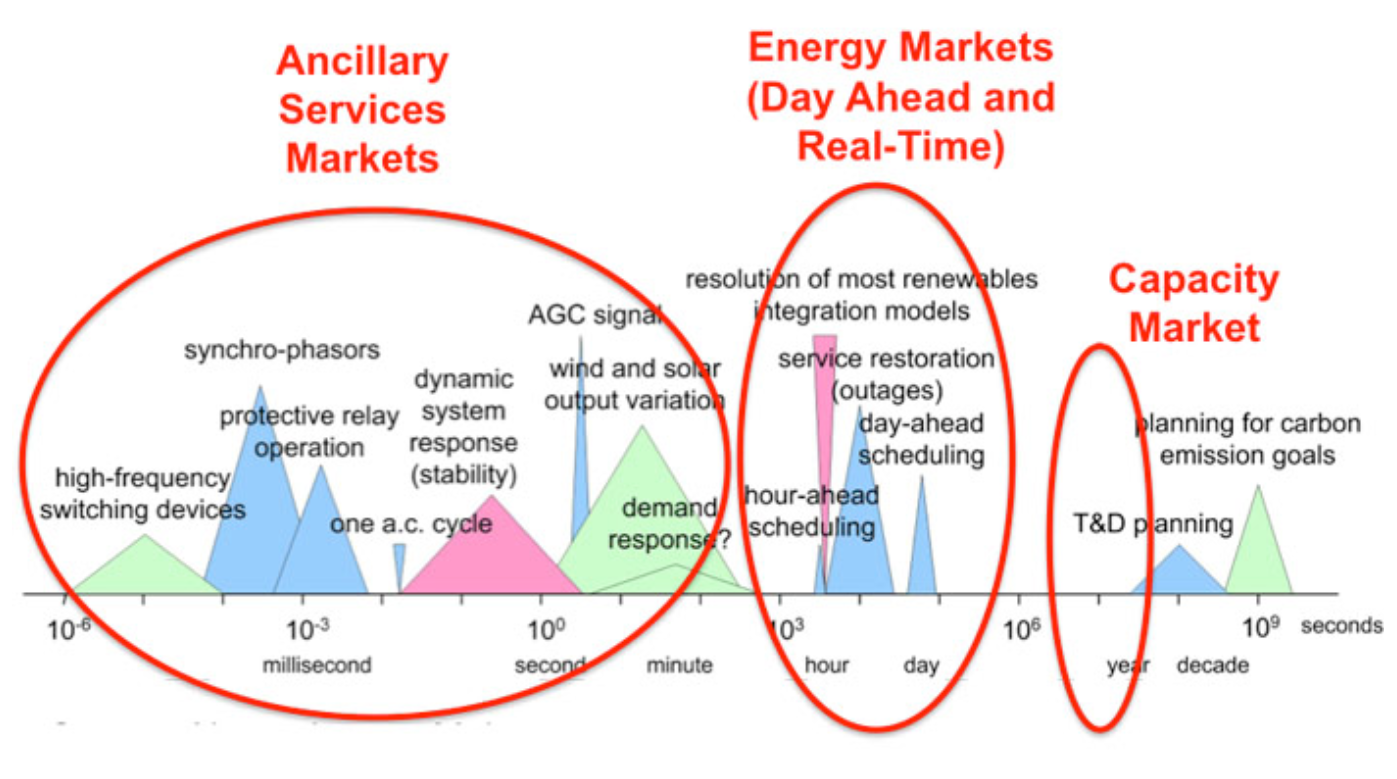
\(Figure \text { } 6.6\): Market constructs used by the RTO to ensure reliability over multiple time scales.

Capacity Markets are meant to provide financial incentives for suppliers to keep generation assets online and to induce new investment in generation. Capacity markets are generally forward markets to have generation capacity online and ready to produce electricity at least one year ahead of time. PJM’s capacity market is run three years ahead of time. For example, a generator that participates in the PJM capacity market in 2012 is effectively making a promise to have generation capacity online and ready to produce in 2015. Capacity markets are thought to be necessary because prices in other RTO markets are not always sufficiently high to keep existing generation from shutting down or to entice new generators to enter the market. Not all RTOs have forward capacity markets. Texas, for example, does not operate a capacity market. We will discuss capacity markets in more detail in Lesson 7.

Energy Markets are perhaps the most well-known of all market constructs run by RTOs. Like capacity markets, energy markets are forward markets but are used by the RTO to ensure that enough generation capacity is online and able to produce energy on a day-ahead (24-hour ahead) to one-hour-ahead basis. RTOs run two types of energy markets. The first, the “day-ahead market” is used to determine which generators are scheduled to operate during each hour of the following day (and at what level of output), based on a projection of electricity demand the following day. The second, the “real-time market” is somewhat poorly named; this market is used by the RTO to adjust which generators are scheduled to run on an hour-ahead basis. A better term for the real-time market (which is used in some cases) would be “adjustment market” or “balancing market” since supplies for this so-called real-time market are actually procured one day in advance (but after supplied are procured through the day-ahead market). The prices prevailing in the day-ahead and real-time markets are the most commonly referenced and quoted of all markets run by the RTOs.

Ancillary Services Markets allow the RTO to maintain a portfolio of backup generation in case of unexpectedly high demand or if contingencies, such as generator outages, arise on the system. There are many different types of ancillary services, corresponding to the speed with which the backup generation needs to be dispatched. “Reserves” represent capacity that can be synchronized with the grid and brought to some operating level within 60, 30, or 15 minutes. “Regulation” represents capacity that can change its level of output within a few seconds in response to fluctuations in the system frequency. Ancillary services are increasingly important for renewable energy integration, so we will discuss those markets in Lesson 7.

Suppliers may participate in multiple markets. For example, a 100 MW generator could offer 80 MW to the day-ahead market, 10 MW to the real-time market, and 5 MW each to the regulation and reserves markets. The generator would earn different payments for each type of service provided to the grid. Thus, while the day-ahead or real-time price is often referred to as “the” market price of electricity, in reality there are many different prices in the RTO market at any given time, each representing a different type of service offered to the RTO.

Because the RTO operates its entire system in an integrated way, even though its footprint may encompass many different utility territories and transmission owners, RTO type markets are sometimes referred to as “power pools” or simply “pools.” The following video contains more information about how the pool-type markets are structured, using the largest pool type model (PJM, in the Mid-Atlantic U.S.).

Video: PJM Model and SMP (9:37)

If you are interested, the following two videos discuss electricity market structures that are alternatives to the pool:

Video: Bilateral Markets Exist in Regions of the U.S. (4:25)

Video: The Power Exchange Model Was Tried for a Couple of Years in California (6:00)

Virtually all RTO markets are operated as “uniform price auctions.” Under the uniform price auction, generators submit supply offers to the RTO, and the RTO chooses the lowest-cost supply offers until supply is equal to the RTO’s demand. This process is called “clearing the market.” The last generator dispatched is called the “marginal unit” and sets the market price. Any generator whose supply offer is below the market-clearing price is said to have “cleared the market,” and is paid the market-clearing price for the amount of supply that cleared the market. Generators with marginal operating costs below the market-clearing price will earn profits. In general, if the market is competitive (all suppliers offer at marginal operating cost) the marginal unit does not earn any profit.

The uniform price auction is illustrated in \(Figure \text { } 6.7\). There are five suppliers, each of which offers its capacity to the market at a different price. These supply offers are shown in \(Table \text { } 6.1\). Here we will assume that supply offers are equal to the marginal costs of each generator, but in the deregulated generation market suppliers are not really obligated to submit offers that are equal to costs. The RTO aggregates these supply offers to form a single market-wide “dispatch stack” or supply curve. Demand is represented by a vertical line (the RTO assumes that demand is fixed, or “perfectly inelastic” with respect to price). In this case, demand is 55 MWh. Generators A, B, C and D clear the market. Generator E does not clear the market since its supply offer is too high. The market-clearing price, known as the “system marginal price (SMP)” would be $40 per MWh. Generators A, B, C, and D would each be paid $40 per MWh. Generators A, B and C would earn profit. Generator D is the marginal unit so it earns zero profit.

\(Table \text { } 6.1\): Suppliers participating in the RTO market

Supplier	Capacity (MW)	Marginal Cost ($/MWh)
A	10	$10
B	15	$15
C	20	$30
D	25	$40
E	10	$70

Let’s calculate the profits for each of our generators. Remember that each generator that clears the market (in this case, it would be A, B, C, and D; E does not clear the market) earns the SMP for each unit of electricity they sell. Total profits are thus calculated as: \[\text { Profit = Output } \times(\text {SMP}-\text { Marginal Cost}).\]

Since the SMP in our example is equal to $40, profits are calculated as: \[\begin{array}{l}
\text { Firm A profit }=10 \times(40-10)=\$ 300 \\
\text { Firm B profit }=15 \times(40-15)=\$ 375 \\
\text { Firm C profit }=20 \times(40-30)=\$ 200 \\
\text { Firm D profit }=10 \times(40-40)=\$ 0 \\
\text { Firm E profit }=0 \times(40-70)=\$ 0
\end{array}\]

Note in particular that Firm D, which is the “marginal unit” setting the SMP of $40/MWh, clears the market but does not earn any profits. We will come back to this case when we discuss capacity markets in Lesson 7.

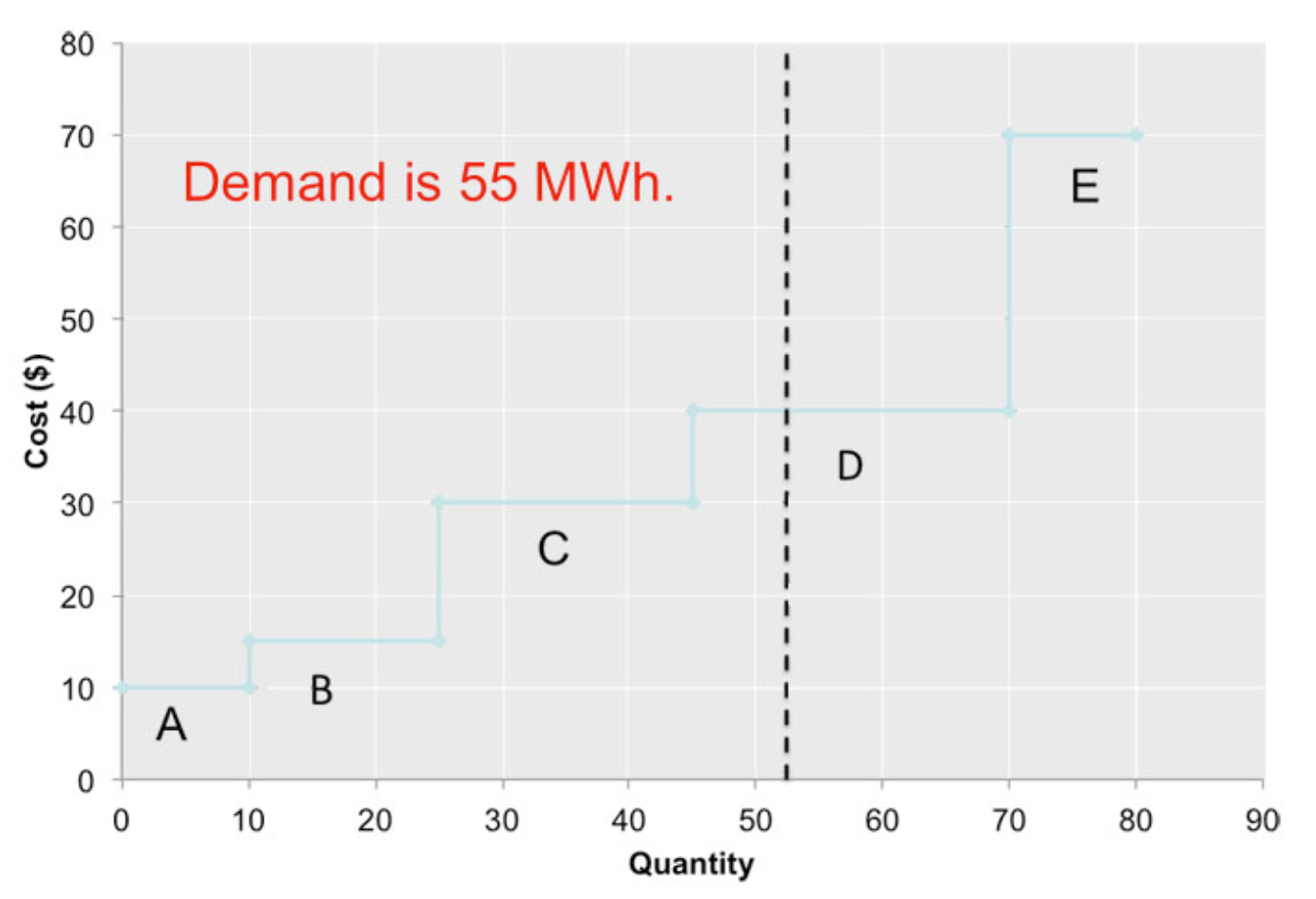
\(Figure \text { } 6.7\): Illustrating the uniform price auction.