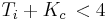10.7: Routh Stability - Ranges of Parameter Values that are Stable
- Page ID
- 22506
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
The stability of a process control system is extremely important to the overall control process. System stability serves as a key safety issue in most engineering processes. If a control system becomes unstable, it can lead to unsafe conditions. For example, instability in reaction processes or reactors can lead to runaway reactions, resulting in negative economic and environmental consequences.
The absolute stability of a control process can be defined by its response to an external disturbance to the system. The system may be considered stable if it exists at a consistent state or setpoint and returns to this state immediately after a system disturbance. In order to determine the stability of a system, one often must determine the eigenvalues of the matrix representing the system’s governing set of differential equations. Unfortunately, sometimes the characteristic equation of the matrix (the polynomial representing its eigenvalues) can be difficult to solve; it may be too large or contain unknown variables. In this situation, a method developed by British mathematician Edward Routh can yield the desired stability information without explicitly solving the equation.
Recall that in order to determine system stability one need only know the signs of the real components of the eigenvalues. Because of this, a method that can reveal the signs without actual computation of the eigenvalues will often be adequate to determine system stability.
To quickly review, negative real eigenvalue components cause a system to return to a steady state point (where all partial derivatives equal zero) when it experiences disturbances. Positive real components cause the system to move away from a stable point, and a zero real component indicates the system will not adjust after a disturbance. Imaginary components simply indicate oscillation with a general trend in accordance with the real part. Using the method of Routh stability, one can determine the number of each type of root and thus see whether or not a system is stable. When unknown variables exist in the equation, Routh stability can reveal the boundaries on these variables that keep the roots negative.
The Routh Array
The Routh array is a shortcut to determine the stability of the system. The number of positive (unstable) roots can be determined without factoring out any complex polynomial.
Generating the Array
The system in question must have a characteristic equation of a polynomial nature. as shown below:
\[P(S) = a_{n}S^n + a_{n-1}S^{n-1} + \cdots + a_{1}S+ a_0 \nonumber \]
In order to examine the roots, set P(S)=0, which will allow you to tell how many roots are in the left-hand plane, right hand plane, and on the j-omega axis. If the system involves trigonometric functions it needs to be fit to a polynomial via a Taylor series expansion. One necessary condition for stability is that 0 \qquad " src="/@api/deki/files/18713/image-273.png">. (If
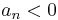 , all coefficients may be multiplied by -1 before checking). The other condition is that all values in column 1 of the Routh array must be positive for the system to be stable.
, all coefficients may be multiplied by -1 before checking). The other condition is that all values in column 1 of the Routh array must be positive for the system to be stable.
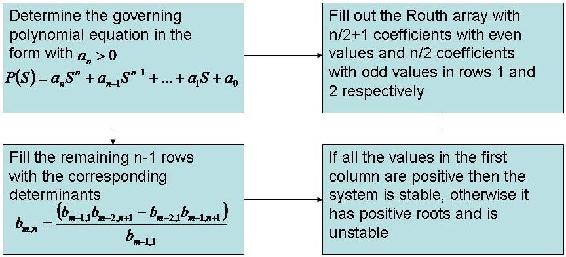
This flow diagram shows the generation of a Routh array for an idealized case with m,n representing the location in the matrix.
The coefficients of the polynomial are placed into an array as seen below. The number of rows is one more than the order of the equation. The number of sign changes in the first column indicate the number of positive roots for the equation.
| Row 1 | \[\\ \ a_{n } \ \ \qquad a_{n-2} \ \qquad a_{n-4} \qquad ... \nonumber \] |
| Row 2 | \[\\ \ a_{n-1} \qquad a_{n-3} \qquad a_{n-5} \qquad ... \nonumber \] |
| Row 3 | \[\\ \ b_1 \qquad \qquad b_2 \ \ \qquad b_3 \ \qquad \ ... \nonumber \] |
| Row 4 | \[\\ \ c_1 \qquad \qquad c_2 \ \ \qquad c_3 \ \qquad \ ... \nonumber \] |
 |
\[\\ \ \vdots \qquad \quad \qquad \vdots \qquad \ \ \ \vdots \; \; \qquad \ \ \vdots \nonumber \] |
| Row 5 | \[\\ \ p_1 \qquad \qquad p_2 \nonumber \] |
| Row 6 | \[\\ \ q_1 \qquad \nonumber \] |
| Row 7 | \[\\ \ v_1 \qquad \nonumber \] |
In the array, the variables b1,b2,c1,c2,etc. are determined by calculating a determinant using elements from the previous two rows as shown below:
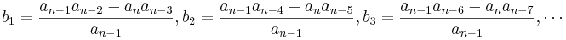
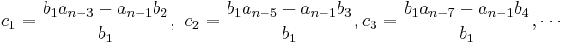
The general expression for any element x after the first two rows with index (m,n) is as follows:
For 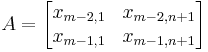
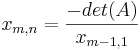
Note, that if the Routh array starts with a zero, it may still be solved (assuming that all the other values in the row are not zero), by replacing the zero with a constant, and letting that constant equal a very small positive number. Subsequent rows within that column that have this constant will be calculated based on the constant choosen.
Once the array is complete, apply the following theorems to determine stability:
- If all of the values in the fist column of the Routh array are >0, then P(S) has all negative real roots and the system is stable.
- If some of the values in the first column of the Routh array are <0, then the number of times the sign changes down the first column will = the number of positive real roots in the \(P(S)\) equation.
- If there is 1 pair of roots on the imaginary axis, both the same distance from the origin (meaning equidistant), then check to see if all the other roots are in the left hand plane. If so, then the imaginary roots location may be found using AS2 + B = 0, where A and B are the elements in the Routh array for the 2nd to last row.
To clarify even further, an example with real numbers is analyzed.
The following polynomial was generated from a sample system.
\[P(S) = 5S^3 -10S^2 + 7S+ 20 \nonumber \]
The preceding polynomial must be investigated in order to determine the stability of the system. This is done by generating a Routh array in the manner described above. The array as a result of this polynomial is,
| Row 1 | \[\\ \ \ 5 \qquad 7 \nonumber \] |
| Row 2 | \[\\ -10 \ \ \ \ 20 \nonumber \] |
| Row 3 | \[\\ \ \ 17 \nonumber \] |
| Row 4 | \[\\ \ \ 20 \nonumber \] |
In the array shown above, the value found in the third row is calculated as follows. 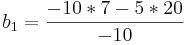 The array can now be analyzed. When looking down the first column, it can be seen that 5 is positive in magnitude, then the sign changes in the -10 entry, and the sign changes a second time to positive 17. This counts as two changes in sign, which corresponds to two positive roots, making the system unstable.
The array can now be analyzed. When looking down the first column, it can be seen that 5 is positive in magnitude, then the sign changes in the -10 entry, and the sign changes a second time to positive 17. This counts as two changes in sign, which corresponds to two positive roots, making the system unstable.
Finding Stable Control Parameter Values
Often, for a unit operation, a PID parameter such as controller gain (Kc), the integral time constant (Ti), or the derivative time constant (Td) creates an additional variable in the characteristic equation. This can be carried through the computations of the Routh array to indicate which values of the variable will provide stability to the system through by preventing positive roots from occuring in the equation. For example, if a controller output is governed by the function:
\[ 10s^3 + 5s^2 + 8s + (T_d + 2) \nonumber \]
The stable values of Td can be found via a Routh array:
| Row 1 | \(\quad 10 \qquad\quad 8\) |
| Row 2 | \(\quad 5 \ \qquad \ \ \ (T_d + 2)\) |
| Row 3 | \( \ \ 4-2T_d\) |
| Row 4 | \((T_d + 2)\) |
We reveal \(-2 < T_d < 2 \qquad \) in order to keep the first column elements positive, so this is the stable range of values for this parameter.
If multiple parameters were in the equation, they would simply be solved for as a group, yielding constraints along the lines of "Ti + Kc > 2" etc, so any value chosen for one parameter would give a different stable range for the other.
Special Cases
There are a few special cases that one should be aware of when using the Routh Test. These variances can arise during stability analysis of different control systems. When a special case is encountered, the traditonal Routh stability solution methods are altered as presented below.
One of the coefficients in the characteristic equation equals zero
If the power of the 0*Sn is 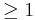 , replace the zero with a quantity, ε, which would be positive and will approach zero. Then continue with your analysis as normal. Essentially this gives the limit of the roots as that coefficient approaches zero. (If the power = 0, see Case 3). For example,
, replace the zero with a quantity, ε, which would be positive and will approach zero. Then continue with your analysis as normal. Essentially this gives the limit of the roots as that coefficient approaches zero. (If the power = 0, see Case 3). For example,
Equation: 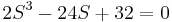
Working Equation: 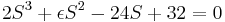
| Row 1 | \[\quad 2 \quad \quad \quad -24 \nonumber \] |
| Row 2 | \[\quad \epsilon \quad \quad \quad 32 \nonumber \] |
| Row 3 | \[\\frac{-24\epsilon-64}{\epsilon} \ \quad \qquad 0 \nonumber \] |
| Row 4 | \[\\qquad 32 \nonumber \] |
Since ε is positive we know that in the first column row 2 will be positive, row 4 will be positive, and row 3 will be negative. This means we will have a sign change from 2 to 3 and again from 3 to 4. Because of this, we know that two roots will have positive real components. If you actually factor out the equation you see that 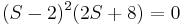 , showing that we do have 2 positive roots. Both of these roots are equal to 2, so there is technically only one root, but in any case we know the system is unstable and must be redesigned.
, showing that we do have 2 positive roots. Both of these roots are equal to 2, so there is technically only one root, but in any case we know the system is unstable and must be redesigned.
One of the roots is zero
This case should be obvious simply from looking at the polynomial. The constant term will be missing, meaning the variable can be factored from every term. If you added an ε to the end as in case 1, the last row would be ε and falsely indicate another sign change. Carry out Routh analysis with the last zero in place.
Equation: 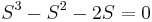
| Row 1 | \[\\ \ 1 \ \ \ -2 \nonumber \] |
| Row 2 | 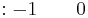 |
| Row 3 | 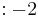 |
| Row 4 | \[\\ \ 0 \qquad \nonumber \] |
As you can see in column one we have row 1 positive, row 2 and 3 negative, and row 4 zero. This is interpreted as one sign change, giving us one positive real root. Looking at this equation in factored form,
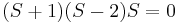
we can see that indeed we have only one positive root equal which equals 2. The zero in the last row indicates an additional unstable root of zero. Alternatively, you may find it easier to just factor out the variable and find the signs of the remaining eigenvalues. Just remember there is an extra root of zero.
Row Full of Zeros
When this happens you know you have either a pair of imaginary roots, or symmetric real roots. The row of zeros must be replaced. The following example illustrates this procedure.
Equation: 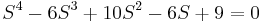
| Row 1 | \[\\ \ 1 \qquad \qquad 10 \qquad \qquad 9 \nonumber \] |
| Row 2 |  |
| Row 3 | \[\\ \ 9 \qquad \qquad 9 \nonumber \] |
| Row 4 | \[\\ \ 0 \qquad \qquad 0 \nonumber \] |
Row 4 contains all zeros. To determine its replacement values, we first write an auxiliary polynomial A determined by the entries in Row 3 above.
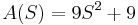
Notice that the order decreases by 1 as we go down the table, but decreases by 2 as we go across.
We then take the derivative of this auxiliary polynomial.
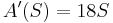
The coefficients obtained after taking the derivative give us the values used to replace the zeros. From there, we can proceed the table calcuations normally. The new table is
| Row 1 | \[\\ \ 1 \qquad \qquad 10 \qquad \qquad 9 \nonumber \] |
| Row 2 |  |
| Row 3 | \[\\ \ 9 \qquad \qquad 9 \nonumber \] |
| Row 4 | \[\\ \ 18 \qquad \qquad 0 \nonumber \] |
| Row 5 | \[\\ \ 9 \qquad \qquad \nonumber \] |
In fact, the purely imaginary or symmetric real roots of the original polynomial are the same as the roots of the auxiliary polynomial. Thus, we can find these roots.
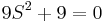
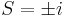
Because we have two sign changes, we know the other two roots of the original polynomial are positive.
In fact, after factoring this polynomial, we obtain
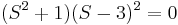
Therefore, the roots are 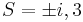 , where in this case, the root 3 has multiplicity 2.
, where in this case, the root 3 has multiplicity 2.
Limitations
Routh arrays are useful for classifying a system as stable or unstable based on the signs of its eigenvalues, and do not require complex computation. However, simply determing the stability is not usually sufficient for the design of process control systems. It is important to develop the extent of stability as well as how close the system is to instability. Further stability analysis not accounted for in the Routh analysis technique include finding the degree of stability, the steady state performance of the control system, and the transient response of the system to disturbances.
More involved techniques, such as those discussed in Eigenvalues and Eigenvectors, must be used to further characterize the system stability (with the exception of system polynomials resulting in pure imaginary roots). Another limitation of the Routh method occurs when the polynomial in question becomes so large that Routh stability is too computationally time consuming (a personal judgment). For this situation another method, such as a root locus plotmust be used.
Note that for defining stability, we will always start out with a polynomial. This polynomial arises from finding the eigenvalues of the linearized model. Thus we will never encounter other functions, say exponenential functions or sin or cos functions in general for stability analysis in control theory.
Advantages Over Root Locus Plots
Routh stability evaluates the signs of the real parts of the roots of a polynomial without solving for the roots themselves. The system is stable if all real parts are negative. Therefore unlike root locus plots, the actual eigenvalues do not need to be calculated for a Routh stability analysis. Furthermore, sometimes the system has too many unknowns to easily construct and interpret a root locus plot (e.g. with two PID controllers there are the variables Kc1, Kc2, τi1, τi2, τd1, and τd2).
Assume the following polynomial describes the eigenvalues of a linearized model of your process. For this polynomial, complete a Routh array and determine the system's stability?
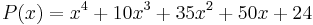
Answer
Since P(X) is a fourth-order polynomial, the Routh array contains five rows.
Row 1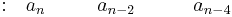 |
Row 2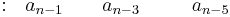 |
Row 3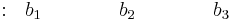 |
Row 4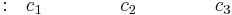 |
Row 5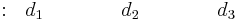 |
Rows 1 and 2 correspond to the coefficients of the polynomial terms:
Row 1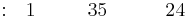 |
Row 2 |
Rows 3, 4, and 5 contain the determinants using elements from the previous two rows.
|
Row 3 |
|
Row 4 |
Row 5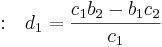 |
Therefore,
|
Row 3 |
|
Row 4 |
Row 5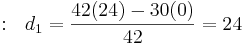 |
The complete Routh array:
Row 1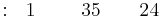 |
Row 2 |
Row 3 |
Row 4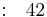 |
Row 5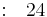 |
Since all the values in the first column are positive, the equation P(x) has all negative roots and the system is stable.
Consider a system with the following characteristic equation:
\[20s^3+59s^2+46s+(4+K_c)=0 \nonumber \]
Using a P-only controller, find the range of controller gain that will yield a stable system.
Answer
Since the equation is a third-order polynomial, the Routh array has four rows. Routh Array:
| Row 1 | \[\\ \qquad \;20 \qquad \qquad \qquad 46 \qquad \nonumber \] |
| Row 2 | \[\\ \qquad \;59 \qquad \qquad \qquad (4+K_c)\qquad \nonumber \] |
| Row 3 | \[\\ \;46 - \frac{20}{59}(4+K_c) \quad \ \quad 0 \nonumber \] |
| Row 4 | \[\\ \ \ \ \ \;(4+K_c) \qquad \qquad \ 0 \nonumber \] |
For the system to be stable, all the elements of the first column of the Routh array have to be positive.
The first column will contain only positive elements if:
0" src="/@api/deki/files/18855/image-349.png">
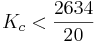
0 \qquad" src="/@api/deki/files/18859/image-351.png">
-4 \qquad" src="/@api/deki/files/18861/image-352.png">
Acceptable stable range 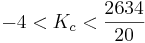
Consider a system with the following characteristic equation:
\[s^5-3s^4+s^3+s^2+4=0 \nonumber \]
Determine the stability of this system.
Answer
One of the coefficients in the characteristic equation equals 0. We replace the zero with a quantity which would be positive (approach zero from the right-hand side) and continue with the analysis as normal.
Working equation:
\[s^5-3s^4+s^3+s^2+ \epsilon s+4=0 \nonumber \]
| Row 1 | \[\\ \ \ 1 \qquad \qquad \qquad \qquad 1\qquad \qquad \epsilon \nonumber \] |
| Row 2 |  |
| Row 3 | \[\\ \frac{4}{3} \ \qquad \qquad \qquad \quad \epsilon + \frac {4}{3} \nonumber \] |
| Row 4 | \[\\ \ 4+ \frac{9\epsilon}{4} \ \qquad \qquad \qquad 4 \nonumber \] |
| Row 5 | \[\\ \epsilon + \frac {4}{3} - \frac{64}{27\epsilon+48} \qquad 0 \nonumber \] |
| Row 6 | \[\\ 4 \nonumber \] |
Since ε is positive, in the first column, there are two sign changes, from row 1 to row 2 and from row 2 to row 3. Thus, we know that the roots will have two positive real components. If you actually factor out the equation you will see that, 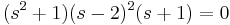 , showing that we do have two positive roots, both equal to 2.
, showing that we do have two positive roots, both equal to 2.
Additional complication exists because at row 5, as ε goes to zero, the term also goes to zero, which means that for row 5, we are getting a row full of zeros. This means that we have a pair of imaginary roots, and this situation can be solved using the equation, 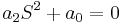 .
.
In this case, the working equation is, 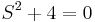
The imaginary roots are, 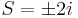
You are an engineer at an icecream factory. There is a storage vat with a cooling system that has a PI controller scheme. It has the following characteristic equation:
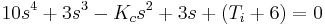
Your job is to determine the constraints on the values Kc and Ti such that the system is stable.
Answer
The goal is to make the matrix such that the first column has no sign changes. Since the first two entries in the first column are numbers and positive, therefore all other values in this column must be positive.
Working equation: 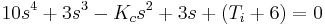
| Row 1 | \[\\ 10 \qquad \qquad \qquad \qquad -K_c \qquad \qquad T_i+6 \nonumber \] |
| Row 2 | \[\\ 3\qquad \qquad \qquad \qquad \qquad 3\qquad \nonumber \] |
| Row 3 | \[\\ 10-K_c \ \qquad \qquad \qquad T_i+6 \nonumber \] |
| Row 4 | \[\\ 3- \frac{3(T_i+6)}{(10-K_c)} \qquad \qquad 0 \nonumber \] |
| Row 5 | \[\\ T_i+6 \nonumber \] |
Since 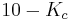 is in the first column, it gives the constraint
is in the first column, it gives the constraint 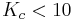 . Likewise,
. Likewise, 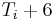 must be positive, giving the constraint
must be positive, giving the constraint -6\," src="/@api/deki/files/18907/image-375.png">. Which brings the final entry of
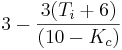 . By dividing by three and rearrangement of the terms, it is seen that
. By dividing by three and rearrangement of the terms, it is seen that 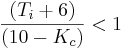 . The terms are then rearranged to arrive at the inequality:
. The terms are then rearranged to arrive at the inequality: 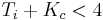 .
.
References
- Bequette, W.B. Process Control Modeling Design and Simulation., New Jersey: Prentice Hall, pp 170-178.
- Foecke, H.A. and Weinstein, A. "Complex roots via real roots and square roots using Routh's stability criterion." arxiv.org, January 5, 2007.
- Liptak, Bela G., Process Control and Optimization. Vol. II. New York: Taylor & Francis.
- Ogunnaike, Babatunde A.; Ray, W. Harmon. Process Dynamics, Modeling, and Control. New York Oxford: Oxford University Press, 1994.
Contributors
- Authors: John D'Arcy, Matt Hagen, Adam Holewinski, and Alwin Ng
- Stewards: Jeff Falta, Taylor Lebeis, Shawn Mayfield, Marc Stewart, Tom Welch



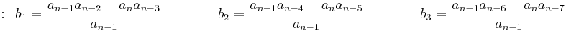

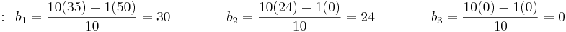
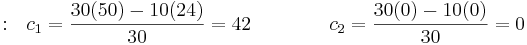
Thus the stable conditions for the constants are:
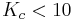
![_i]() -6\," src="/@api/deki/files/18907/image-375.png">
-6\," src="/@api/deki/files/18907/image-375.png">