12.1: Determining if a system can be decoupled
- Page ID
- 22653
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Authors: Wen Chung Lim, James Bennett, Jamila Grant, Ajay Bhasin
Introduction
A system of inputs and outputs can be described as one of four types: SISO (single input, single output), SIMO (single input, multiple output), MISO (multiple input, single output), or MIMO (multiple input, multiple output).
Multiple input, multiple output (MIMO) systems describe processes with more than one input and more than one output which require multiple control loops. Examples of MIMO systems include heat exchangers, chemical reactors, and distillation columns. These systems can be complicated through loop interactions that result in variables with unexpected effects. Decoupling the variables of that system will improve the control of that process.
An example of a MIMO system is a jacketed CSTR in which the formation of the product is dependent upon the reactor temperature and feed flow rate. The process is controlled by two loops, a composition control loop and a temperature control loop. Changes to the feed rate are used to control the product composition and changes to the reactor temperature are made by increasing or decreasing the temperature of the jacket. However, changes made to the feed would change the reaction mass, and hence the temperature, and changes made to temperature would change the reaction rate, and hence influence the composition. This is an example of loop interactions. Loop interactions need to be avoided because changes in one loop might cause destabilizing changes in another loop. To avoid loop interactions, MIMO systems can be decoupled into separate loops known as single input, single output (SISO) systems. Decoupling may be done using several different techniques, including restructuring the pairing of variables, minimizing interactions by detuning conflicting control loops, opening loops and putting them in manual control, and using linear combinations of manipulated and/or controlled variables. If the system can’t be decoupled, then other methods such as neural networks or model predictive control should be used to characterize the system.
There are two ways to see if a system can be decoupled. One way is with mathematical models and the other way is a more intuitive educated guessing method. Mathematical methods for simplifying MIMO control schemes include the relative gain array (RGA) method, the Niederlinski index (NI) and singular value decomposition (SVD). This article will discuss the determination of whether a MIMO control scheme can be decoupled to SISO using the SVD method. It will also discuss a more intuitive way of decoupling a system using a variation of the RGA method.
Definitions of Input and Output System Types
1. SISO- Single Input, Single Output

These systems use data/input from one sensor to control one output. These are the simplest to design since they correspond one sensor to one actuator. For example, temperature (TC) is used to control the valve state of v1 through a PID controller.
2. SIMO- Single Input, Multiple Output
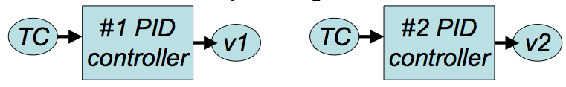
These systems use data/input from one sensor to control multiple outputs. For example, temperature (TC) is used to control the valve state of v1 and v2 through PID controllers.
3. MISO- Multiple Input, Single Output
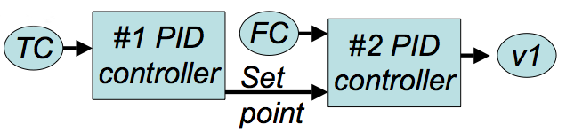
These systems use data/input from multiple sensors to control one ouput. For example, a cascade controller can be considered MISO. Temperature (TC) is used in a PID controller (#1) to determine a flow rate set point i.e. FCset. With the FCset and FC controller, they are used to control the valve state of v1 through a PID controller (#2).
4. MIMO- Multiple Input, Multiple Output
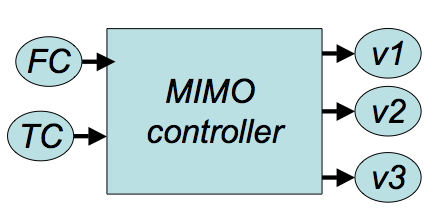
These systems use data/input from multiple sensors to control multiple outputs. These are usually the hardest to design since multiple sensor data is integrated to coordinate multiple actuators. For example, flow rate (FC) and temperature (TC) are used to control multiple valves (v1, v2, and v3). Often, MIMO systems are not PID controllers but rather designed for a specific situation.
Singular Value Decomposition
Singular value decomposition is a useful mathematical way to determine if a system will be prone to interactions due to sensitivity problems that result from small errors in process gains. It is a matrix technique that determines if a system is able to be decoupled.
Two input two output system
The SVD method starts with the steady state gain matrix, which is obtained from the relative gain array (RGA) method for a given 2 input-2 output control loop system:
![[G] = \begin{bmatrix} g_{1,1} & g_{1,2}
\\ g_{2,1} & g_{2,2} \\
\end{bmatrix}](https://eng.libretexts.org/@api/deki/files/18984/image-439.png?revision=1) ,
,
Using [G], we obtain the eigenvalues for the system. This can be done through two methods; either the eigenvalues can be obtained through numerical software as described in the Eigenvalues and Eigenvectors section or the eigenvalues can be calculated by hand. The hand calculations are shown here. [G] gives the following values for the system, which have been derived from theoretical work and are used to find the eigenvalues:
b = g112 + g122 --------------(1)
c = g11g21 + g12g22---------(2)
d = g212 + g222--------------(3)
b, c, and d are parameters created for this method that do not have a direct physical meaning. Using the formulas below with the values of b, c, and d gives the eigenvalues for the system:
λ1 = s12 = 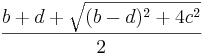 ------(4)
------(4)
λ2 = s22 = 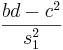 ------(5)
------(5)
s1 and s2 are the positive square roots of the respective eigenvalues. The condition number CN is defined as the ratio of the larger of the two values to the smaller value:
CN = 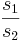 if
if 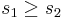 , or CN =
, or CN = 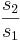 if
if 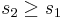
The greater the CN value, the harder it is for the system in question to be decoupled. As a rule of thumb, a system with a CN number of more than 50 is impossible to decouple. Such a system has manipulated variables which all have significant and similar relative impact on the controlled variables they affect and hence the control equations for the system cannot be restructured to obtain a simpler control system. In the worst case scenario for a two input two output system, using the exact same control variable twice would give a CN number of infinity, because both control variables would have the same effect on the controlled variables. An ideal system would have a CN number of one, where each control variable controls a single distinct output variable.
MIMO systems with two or more inputs and outputs
To use this method, it is necessary to know how to create a transpose matrix. A transpose matrix is created by writing the columns of the original matrix as the rows of the transpose matrix. Mathematically, the transpose matrix is denoted by [A]T, where [A] is the original matrix. An example is shown here: 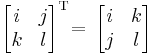
To use singular value decomposition on systems with two or more inputs and outputs, the m x m steady state gain matrix [G] of the form
\[\([G]=\left[\begin{array}{cccc}g_{1,1} & g_{1,2} & \cdots & g_{1, m} \\ g_{2,1} & g_{2,2} & \cdots & g_{2, m} \\ \vdots & & & \\ g_{n, 1} & g_{n, 2} & \cdots & g_{n, m}\end{array}\right]\) \nonumber \]
is broken down into the form:
\[\(G=U \Sigma V^{\top}\) \nonumber \]
where:
- U is an m x m matrix , the column vectors of which are the unit eigenvectors of the m x m matrix GGT,GT being the transpose matrix of G.
- V is an m x m matrix, the column vectors of which are the unit eigenvectors of the m x m matrix GTG.
- Σ is an m x m diagonal matrix containing singular values, where the values are arranged in descending order from the top left most corner to the bottom right corner.
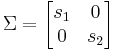 for a 2 input 2 output system if
for a 2 input 2 output system if 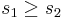 , or
, or 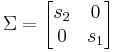 for a 2 input 2 output system if
for a 2 input 2 output system if 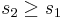 .
.
The CN number can then be determined by the ratio of the largest value in Σ to the smallest value. Notice in the previous two input two output example, there was no need to calculate the eigenvalue matrix Σ for a two by two matrix, since the eigenvalues can be calculated directly with the parameters b,c, and d.
For more information on how to derive the three matrices U, Σ and V by hand, refer to the Eigenvalues and Eigenvectors section.
Mathematica can also be used to find U, Σ and V for a given m x m Matrix G. This is accomplished by typing in the command
Map[MatrixForm, {u, w, v}=SingularValueDecomposition[G]],
giving U, Σ and V in that order.
Intuitive decoupling using the RGA
With this technique, the first step is to construct the RGA by placing all of the controllers in manual, changing the value of the output manually, and then recording the final value of the controller after making the change. This will give the gain matrix, which is then multiplied by its inverse to give the relative gain matrix. The goal here is to pair measurements and control valves so that the relative gain elements are close to 1, and all other combinations are close to zero. A values between 0 and 1 tells that the net effect of the other loops on this pairing is to change the measurement signal in the same direction as the control valve signal (cooperation). A value greater than one means that the measurement signal will go in the opposite direction of the control valve signal (conflict). Finally a relative gain element less than zero means that the net effect is conflict, but here the gain will change sign, not the measurement signal. Therefore, if a loop is stable when the other loops are in manual, it will probably not be stable when the other loops are in automatic, and vice versa. To intuitively decouple this system then would require a guess and check of different pairings, with the goal being to get the pairings to a relative gain element close to one. If this is not possible and no pairings give a value close to one, then the system will need to be decoupled using decoupling control.
Decoupling a system using decoupling control
The goal of decoupling control is to eliminate complicated loop interactions so that a change in one process variable will not cause corresponding changes in other process variables. To do this a non-interacting or decoupling control scheme is used. In this scheme, a compensation network called a decoupler is used right before the process. This decoupler is the inverse of the gain array and allows for all measurements to be passed through it in order to give full decoupling of all of the loops. This is shown pictorially below.
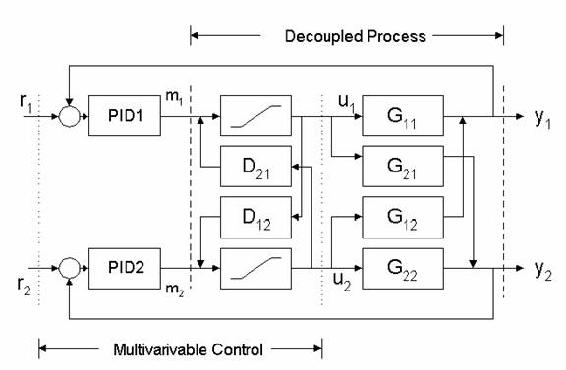
For a simple jacketed reactor example, if changing the flow rate of reactant to obtain a desired composition also increases the reactor temperature by five degrees, the decoupler would decrease the temperature of the jacket to decrease the temperature inside the reactor by five degrees, offsetting the original change. This jacket temperature decrease also changes the composition inside the reactor, so a properly designed controller accounts for both effects in the control scheme to obtain the desired composition without changing the reactor temperature.
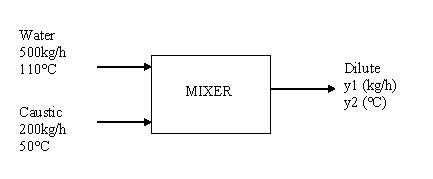
Worked out Example 1
Hot water at 110°C is pumped into a mixer at 500 kg/h. The water is used to dilute a concentrated caustic substance at 50°C flowing in at 200 kg/h. Below is a diagram of the process. Check, by the singular value decomposition method, to see if decoupling of the system is feasible. Assume that the heat capacities of both streams are the same with no heat of mixing.
\[\\bold{Solution:} \nonumber \]
From the question you know:
T1 = 383.15 K
T2 = 323.15 K
m1 = 500 kg/h
m2 = 200 kg/h
y1 = outgoing mass flow rate (kg/h)
y2 = temperature of outflowing stream (K)
From mass balances you know:
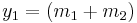
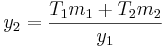
So:
y1 = 700 kg/h
y2 = 366.01 K
The steady state gain matrix (G) needs to be calculated as explained in the RGA method:
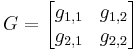
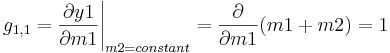
![g_{2,1}= \frac{\partial y2}{\partial m1} \Bigg|_{m2=constant} = \frac{\partial}{\partial m1} \left ( \frac{T1m1 + T2m2}{m1 + m2} \right ) = \left [ \frac{(T1-T2)m2}{(m1+m2)^2} \right ]](https://eng.libretexts.org/@api/deki/files/19018/image-455.png?revision=1)
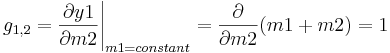
![g_{2,2}= \frac{\partial y2}{\partial m2} \Bigg|_{m1=constant} = \left [ \frac{(T2-T1)m1}{(m1+m2)^2} \right ]](https://eng.libretexts.org/@api/deki/files/19020/image-457.png?revision=1)
By plugging in all known values, the steady state gain matrix becomes:
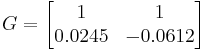
From here you can solve for the values b, c, d λ1, λ2, s1 and s2 by using the equations (1) through (5) in the wiki:
b = g112 + g122 = 12 + 12 = 2
c = g11g21 + g12g22 = (1)(.0245) + (1)( − .0612) = -0.0367
d = g212 + g222 = .02452 + − .06122 = 0.004346
λ1 = 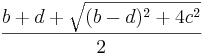 =
= 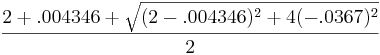 = 2
= 2
λ2 = 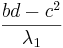 =
= 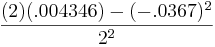 = 0.003673
= 0.003673
s1 = 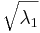 =
= 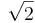 = 1.414
= 1.414
s2 = 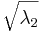 =
= 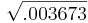 = 0.0606
= 0.0606
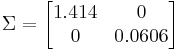
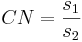 = 23.33
= 23.33
CN is less than 50, therefore decoupling for this system is feasible.
Worked out Example 2
A jacketed reactor with a single feed stream (Stream 1) is monitored by 3 proportional (P) controllers as indicated in the figure.
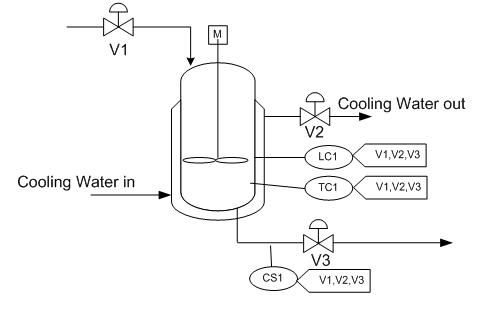
These controllers all act as inputs to each of 3 valves according to the relationships:
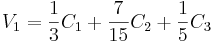
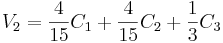
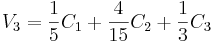
Where:
C1 = Kc1e1(t) + b1, C1 is the output from the level controller
C2 = Kc2e2(t) + b2, C2 is the output from the temperature controller
C3 = Kc3e3(t) + b3, C3 is the output from the composition sensor
Is it feasible to decouple this system?
\[\\bold{Solution:} \nonumber \]
The gain array is calculated according to the RGA method and is:
Input the following commands in Mathematica for SVD analysis:
G =
Callstack:
at (Bookshelves/Industrial_and_Systems_Engineering/Chemical_Process_Dynamics_and_Controls_(Woolf)/12:_Multiple_Input_Multiple_Output_(MIMO)_Control/12.01:_Determining_if_a_system_can_be_decoupled), /content/body/div[4]/p[16]/span, line 1, column 4
The output of the SVD decomposition is the following:
 ,
, 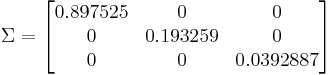 ,
, 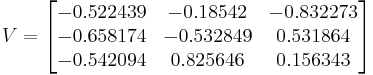
The condition number is calculated from the highest and lowest values of the ∑ matrix:
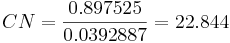
CN < 50, therefore the system may be decoupled.
As a more complicated problem, consider how this problem would change if the controllers used a cascade control style. For a P controller, the output may be similar to:
C2 = Kc2e2(t) + b2 = Kc2 * (LCactual − f(C1)) + b
What if we used a PID controller instead?
Multiple Choice Question 1
The CN, or condition number
a. Is the ratio of the smaller number (s2) to the larger number (s1)
b. Determines the feasibility of decoupling a system.
c. Is the unit eigenvectors of the m x m matrix GTG
d. Is always less than 50.
Answer: b
Multiple Choice Question 2
For MIMO systems
a. Control loops are isolated
b. Each controlled variable is only manipulated by one variable
c. Decoupling the system makes it more complicated
d. Manipulated variables may affect several controlled variables
Answer: d
Sage's Corner
www.youtube.com/v/j-heeeVmEAM
Unnarated Powerpoint Presentation
References
- Mahoney, D.P., Svrcek, W.Y., and Young, B.R. (2006) A Real-Time Approach to Process Control, 2nd Edition. John Wiley & Sons, Ltd. ISBN 0470025336
- Gwak, K.W., Masada, G.Y. (2005) "Structural Analysis and Optimization of Nonlinear Control Systems Using Singular Value Decomposition". American Society of Mechanical Engineers Journal of Dynamic Systems, Measurement and Control, Vol. 127, No. 1, pp. 105-113, March 2005.
- McMillan, Gregory K. (1983) Tuning and Control Loop Performance. Instrument Society of America. ISBN 0-87664-694-1.
- Tham, M.T. (1999). "Multivariable Control: An Introduction to Decoupling Control". Department of Chemical and Process Engineering, University of Newcastle upon Tyne. Available online at: lorien.ncl.ac.uk/ming/mloop/mloop.pdf.
- Lee, Jay H., Choi, Jin Hoon, and Lee, Kwang Soon. (1997). "3.2 Interaction and I/O Pairing". Chemical Engineering Research Information Center. Available online at: www.cheric.org/education/practical/mpc16473.pdf.


