14.2.1.1: Algebraic Expressions and Formulas

Last updated
Save as PDF

Page ID: 67463

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Identify the parts of an algebraic expression.
Apply the distributive property.
Evaluate algebraic expressions.
Use formulas that model common applications.

Algebraic Expressions and the Distributive Property

In algebra, letters called variables are used to represent numbers. Combinations of variables and numbers along with mathematical operations form algebraic expressions, or just expressions. The following are some examples of expressions with one variable, $x$:

Table $\PageIndex{1}$
$2x+3$	$x^{2}−9$	$\frac{1}{x}+\frac{x}{x+2}$	$3\sqrt{x}+x$

Terms in an algebraic expression are separated by addition operators and factors are separated by multiplication operators. The numerical factor of a term is called the coefficient. For example, the algebraic expression $x^{2} y^{2} + 6xy − 3$ can be thought of as $x^{2} y^{2} + 6xy + (−3)$ and has three terms. The first term, $x^{2} y^{2}$, represents the quantity $1x^{2} y^{2} = 1 ⋅ x ⋅ x ⋅ y ⋅ y$ where $1$ is the coefficient and x and y are the variables. All of the variable factors with their exponents form the variable part of a term. If a term is written without a variable factor, then it is called a constant term. Consider the components of $x^{2} y^{2} + 6xy − 3$,

Table $\PageIndex{2}$
*Terms*	*Coefficient*	*Variable Part*
$x^{2}y^{2}$	$1$	$x^{2}y^{2}$
$6xy$	$6$	$xy$
$−3$	$−3$

The third term in this expression, $−3$, is called a constant term because it is written without a variable factor. While a variable represents an unknown quantity and may change, the constant term does not change.

Example $\PageIndex{1}$:

List all coefficients and variable parts of each term: $10a^{2}−5ab−b^{2}$.

Solution

We want to think of the third term in this example $−b^{2}$ as $−1b^{2}$.

Table $\PageIndex{3}$
*Terms*	*Coefficient*	*Variable Part*
$10a^{2}$	$10$	$a^{2}$
$−5ab$	$−5$	$ab$
$−b^{2}$	$−1$	$b^{2}$

Answer: Coefficients: $\{−5, −1, 10\}$; Variable parts: $\{a^{2}, ab, b^{2}\}$

In our study of algebra, we will encounter a wide variety of algebraic expressions. Typically, expressions use the two most common variables, $x$ and $y$. However, expressions may use any letter (or symbol) for a variable, even Greek letters, such as alpha ($\alpha$) and beta ($\beta$). Some letters and symbols are reserved for constants, such as $π ≈ 3.14159$ and $e ≈ 2.71828$. Since there is only a limited number of letters, you will also use subscripts, $x_{1} , x_{2} , x_{3} , x_{4} , …,$ to indicate different variables.

The properties of real numbers are important in our study of algebra because a variable is simply a letter that represents a real number. In particular, the distributive property states that if given any real numbers $a, b$ and $c$, then,

$\color{Cerulean}{a}$ $ ( b + c ) = \color{Cerulean}{a}$$b + \color{Cerulean}{a}$$c$

This property is one that we apply often when simplifying algebraic expressions. To demonstrate how it will be used, we simplify $2(5 − 3)$ in two ways, and observe the same correct result.

Table $\PageIndex{4}$
*Working parenthesis first.*	*Using the distributive property.*
$ 2(\color{OliveGreen}{5−3}$$)=2(2)$ $=4$	$ 2(5−3)=$$\color{Cerulean}{2}$$⋅5−\color{Cerulean}{2}$$⋅3$ $=10−6$ $=4$

Certainly, if the contents of the parentheses can be simplified we should do that first. On the other hand, when the contents of parentheses cannot be simplified any further, we multiply every term within it by the factor outside of it using the distributive property. Applying the distributive property allows us to multiply and remove the parentheses.

Example $\PageIndex{2}$:

Simplify: $5(−2a+5b)−2c$.

Solution

Multiply only the terms grouped within the parentheses for which we are applying the distributive property.

Example of distributive process where the 5 is multiplied by each term in the parentheses.

$=\color{Cerulean}{5}$$⋅(−2a)+\color{Cerulean}{5}$$⋅5b−2c$

$=−10a+25b−2c$

Answer: $−10a+25b−2c$

Recall that multiplication is commutative and therefore we can write the distributive property in the following manner, $(b + c) a = ba + ca$.

Example $\PageIndex{3}$:

Simplify: $(3x−4y+1)⋅3$.

Solution

Multiply all terms within the parenthesis by $3$.

$(3x−4y+1)⋅3=3x\color{Cerulean}{⋅3}$$−4y\color{Cerulean}{⋅3}$$+1\color{Cerulean}{⋅3}$

$=9x−12y+3$

Answer: $9x−12y+3$

Terms whose variable parts have the same variables with the same exponents are called like terms, or similar terms. Furthermore, constant terms are considered to be like terms. If an algebraic expression contains like terms, apply the distributive property as follows:

$5 \color{Cerulean}{x}$$ + 7 \color{Cerulean}{x}$$ = ( 5 + 7 ) \color{Cerulean}{x}$$ = 12 \color{Cerulean}{x}$

In other words, if the variable parts of terms are exactly the same, then we can add or subtract the coefficients to obtain the coefficient of a single term with the same variable part. This process is called combining like terms. For example,

$12 x ^ { 2 } y ^ { 3 } + 3 x ^ { 2 } y ^ { 3 } = 15 x ^ { 2 } y ^ { 3 }$

Notice that the variable factors and their exponents do not change. Combining like terms in this manner, so that the expression contains no other similar terms, is called simplifying the expression¹. Use this idea to simplify algebraic expressions with multiple like terms.

Example $\PageIndex{4}$:

Simplify:

$x ^ { 2 } - 10 x + 8 + 5 x ^ { 2 } - 6 x - 1$.

Solution

Identify the like terms and add the corresponding coefficients.

Answer: $6 x ^ { 2 } - 16 x + 7$

Example $\PageIndex{5}$:

Simplify: $a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right)$.

Solution

Distribute $−2$ and then combine like terms.

Answer: $- 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2$

Evaluating Algebraic Expressions

An algebraic expression can be thought of as a generalization of particular arithmetic operations. Performing these operations after substituting given values for variables is called evaluating. In algebra, a variable represents an unknown value. However, if the problem specifically assigns a value to a variable, then you can replace that letter with the given number and evaluate using the order of operations.

Example $\PageIndex{9}$:

Evaluate $\sqrt { b ^ { 2 } - 4 a c }$ where $a = −1, b = −7$, and $c = \frac{1}{4}$.

Solution

Substitute in the appropriate values and then simplify.

$\begin{aligned} & =\sqrt { 49 + 4(\frac{1}{4}) } \\ & = \sqrt { 49 + 1 } \\ & =\sqrt{50} \\& = \sqrt { 25 \cdot 2 } \\ & = 5 \sqrt { 2 } \end{aligned}$

Aligned: $5 \sqrt { 2 }$

Exercise $\PageIndex{1}$

Evaluate $\frac { \sqrt { 3 \pi V h } } { \pi h }$ where $V = 25\pi$ and $h = 3$.

Answer: $5$

Using Formulas

The main difference between algebra and arithmetic is the organized use of variables. This idea leads to reusable formulas, which are mathematical models using algebraic expressions to describe common applications. For example, the volume of a right circular cone depends on its radius $r$ and height $h$ and is modeled by the formula:

$V = \frac { 1 } { 3 } \pi r ^ { 2 } h$

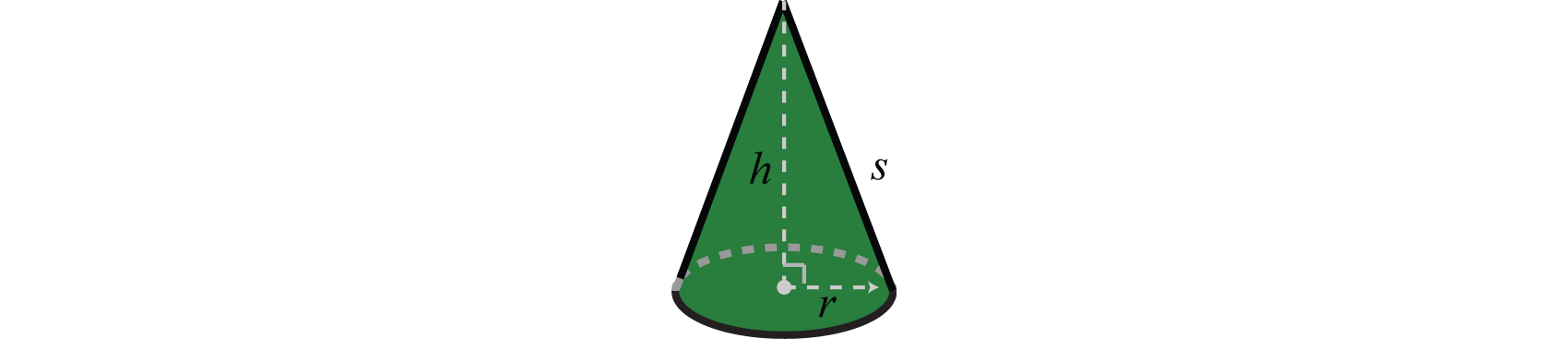
Image of a cone with height h, radius r, and side length s. — Figure $\PageIndex{1}$: Cone with height h, radius r, and side length s.

In this equation, variables and constants are used to describe the relationship between volume and the length of the base and height. If the radius of the base measures $3$ meters and the height measures $5$ meters, then the volume can be calculated using the formula as follows:

$\begin{aligned} V & = \frac { 1 } { 3 } \pi r ^ { 2 } h \\ & = \frac { 1 } { 3 } \pi ( 3 m ) ^ { 2 } ( 5 m ) \\ & = \frac { 1 } {\bcancel {3}} \pi \cdot \stackrel{\color{Cerulean}{3}}{\bcancel{9}} \cdot 5 m ^ { 3 } \\ & = 15 \pi \mathrm { m } ^ { 3 } \end{aligned}$

Using $π ≈ 3.14$, we can approximate the volume: $V ≈ 15 (3.14) = 47.1$ cubic meters.

Formulas for areas and perimeters of common plane figures

A list of formulas that describe the area and perimeter of common plane figures follows. The letter P represents perimeter and is measured in linear units. The letter A represents area and is measured in square units.

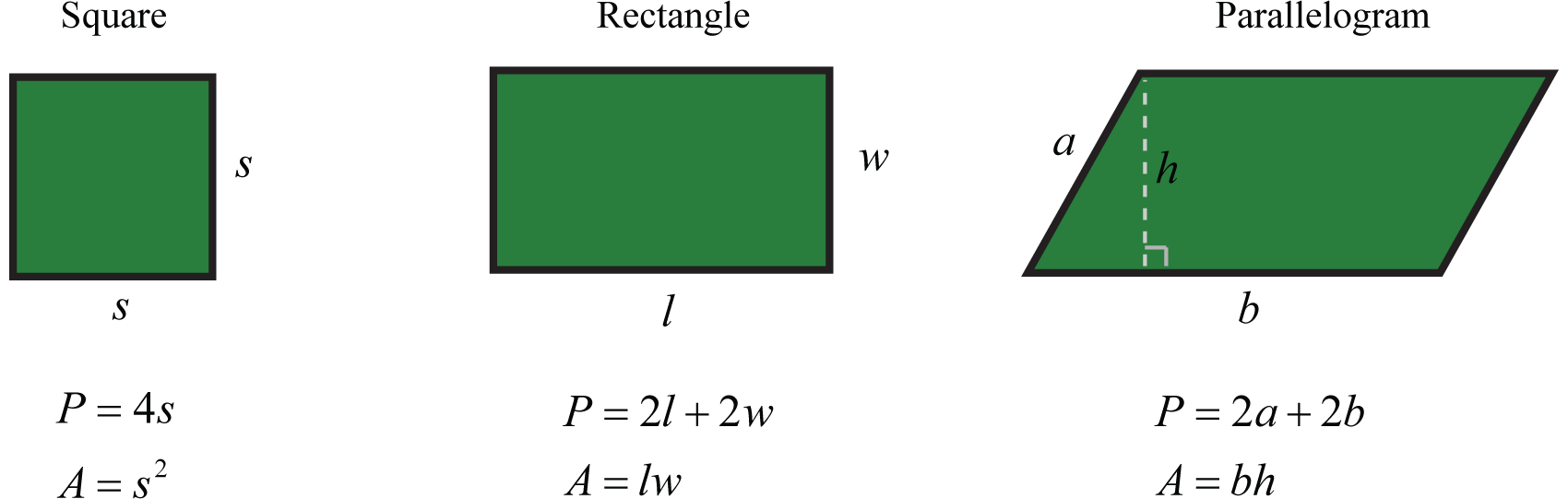
Figure $\PageIndex{2}$: Square, rectangle, and parallelogram formulas for perimeter and area.

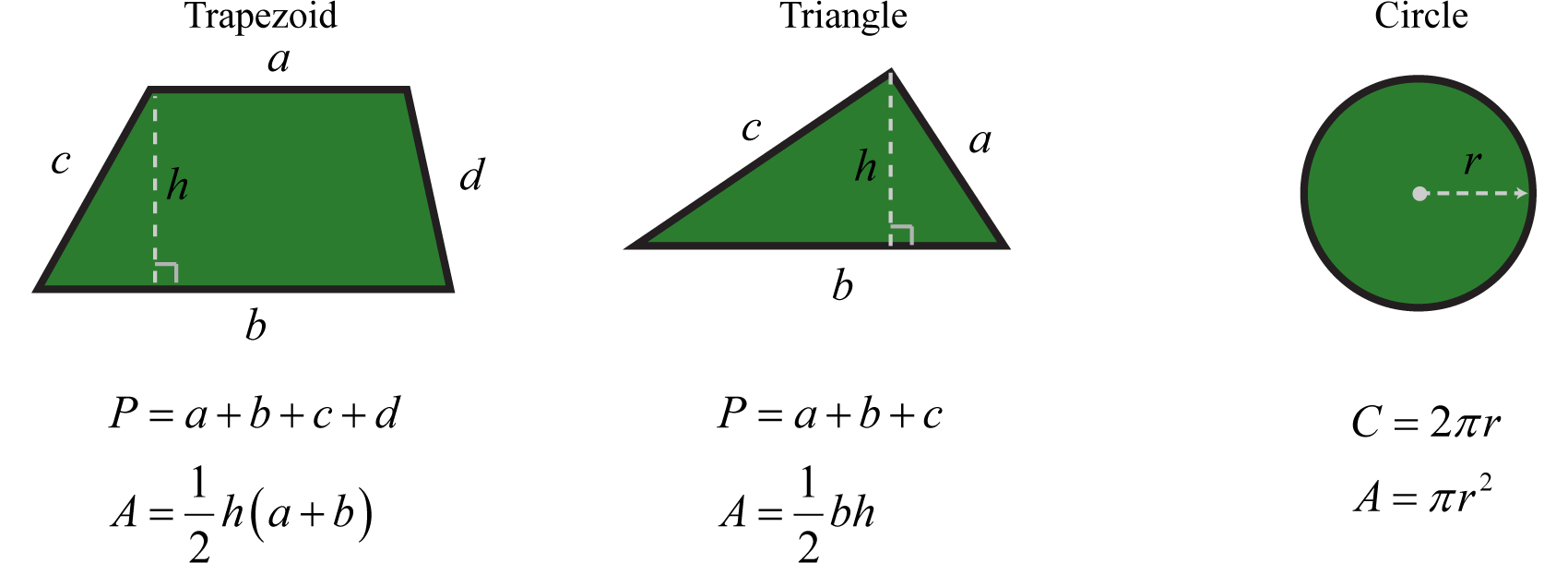
Figure $\PageIndex{3}$: Trapezoid, Triangle, Circle formulas for perimeter and area.

List of formulas for surface area and volume for common figures

A list of formulas that describe the surface area and volume of common figures follows. Here SA represents surface area and is measured in square units. The letter V represents volume and is measured in cubic units.

Figure $\PageIndex{4}$: Cube, rectangular solid, and right circular cylinder formulas for volume and surface area.

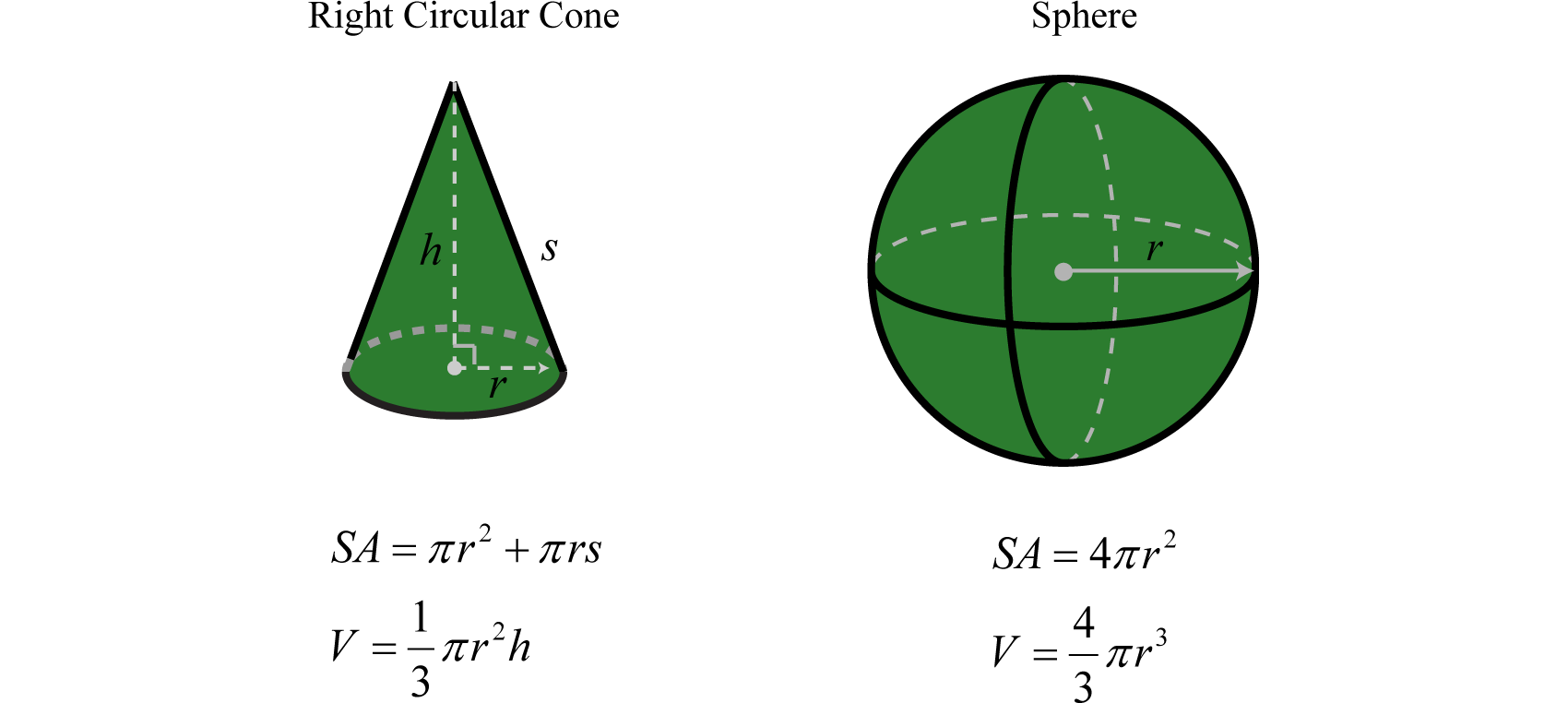
Figure $\PageIndex{5}$: Right circular cone and sphere formulas for volume and surface area.

Example $\PageIndex{10}$:

The diameter of a spherical balloon is $10$ inches. Determine the volume rounded off to the nearest hundredth.

Solution

The formula for the volume of a sphere is

$V = \frac { 4 } { 3 } \pi r ^ { 3 }$

This formula gives the volume in terms of the radius, $r$. Therefore, divide the diameter by $2$ and then substitute into the formula. Here, $r = \frac{10}{2} = 5$ inches and we have

$\begin{aligned} V & = \frac { 4 } { 3 } \pi r ^ { 3 } \\ & = \frac { 4 } { 3 } \pi ( 5 \mathrm { in } ) ^ { 3 } \\ & = \frac { 4 } { 3 } \pi \cdot 125 \mathrm { in } ^ { 3 } \\ & = \frac { 500 \pi } { 3 } \mathrm { in } ^ { 3 } \approx 523.60 \mathrm { in } ^ { 3 } \end{aligned}$

Answer: The volume of the balloon is approximately $523.60$ cubic inches.

Uniform motion

Formulas can be found in a multitude of subjects. For example, uniform motion is modeled by the formula $D = rt$, which expresses distance $D$, in terms of the average rate, or speed, $r$ and the time traveled at that rate, $t$. This formula, $D = rt$, is used often and is read, “distance equals rate times time.” Note we use here speed, not velocity as we have not yet introduced vectors.

Example $\PageIndex{11}$:

Jim’s road trip took $2\:\frac{1}{2}$ hours at an average speed of $66$ miles per hour. How far did he travel?

Solution

Substitute the appropriate values into the formula and then simplify.

$\begin{aligned} D & = r \cdot t \\ & = ( \color{Cerulean}{66 \frac { \mathrm { mi } } { \mathrm { hr } }}\color{Black}{ ) \cdot (}\color{Cerulean}{ 2 \frac { 1 } { 2 } \mathrm { hr }}\color{Black}{)} \\ & = \frac { 66 } { 1 } \cdot \frac { 5 } { 2 } \mathrm { mi } \\ & = 33 \cdot 5 \mathrm { mi } \\ & = 165 \mathrm { mi } \end{aligned}$

Answer: Jim traveled $165$ miles.

Simple interest $I$ is given by the formula $I = prt$, where $p$ represents the principal amount invested at an annual interest rate $r$ for $t$ years.

Example $\PageIndex{12}$:

Calculate the simple interest earned on a $2$-year investment of $$1,250$ at an annual interest rate of $3\:\frac{3}{4} %$.

Solution

Convert $3\:\frac{3}{4}%$ to a decimal number before using it in the formula.

$r = 3 \frac { 3 } { 4 } \% = 3.75 \% = 0.0375$

Use this and the fact that $p = $1,250$ and $t = 2$ years to calculate the simple interest.

$\begin{aligned} I & = p r t \\ & = ( \color{Cerulean}{1,250}\color{Black}{ ) (}\color{Cerulean}{ 0.0375}\color{Black}{ ) (}\color{Cerulean}{ 2}\color{Black}{ )} \\ & = 93.75 \end{aligned}$

Answer: The simple interest earned is $$93.75$.

¹Note that combining like terms is relevant to units as well, following the same rules. For instance, cm + cm² are not like terms and can't be added but cm² + cm² are like terms and can be added together.

*Terms*	*Coefficient*	*Variable Part*
\(x^{2}y^{2}\)	\(1\)	\(x^{2}y^{2}\)
\(6xy\)	\(6\)	\(xy\)
\(−3\)	\(−3\)

*Terms*	*Coefficient*	*Variable Part*
\(10a^{2}\)	\(10\)	\(a^{2}\)
\(−5ab\)	\(−5\)	\(ab\)
\(−b^{2}\)	\(−1\)	\(b^{2}\)