14.2.1.3: Roots and Radicals
- Page ID
- 67462
Square and Cube Roots
Recall that a square root1 of a number is a number that when multiplied by itself yields the original number. For example, \(5\) is a square root of \(25\), because \(5^{2} = 25\). Since \((−5)^{2} = 25\), we can say that \(−5\) is a square root of \(25\) as well. Every positive real number has two square roots, one positive and one negative. For this reason, we use the radical sign \(√\) to denote the principal (nonnegative) square root2 and a negative sign in front of the radical \(−√\) to denote the negative square root.
Zero is the only real number with one square root.
\(\sqrt { 0 } = 0 \text { because } 0 ^ { 2 } = 0\)
If the radicand3, the number inside the radical sign, can be factored as the square of another number, then the square root of the number is apparent. In this case, we have the following property:
\(\sqrt { a ^ { 2 } } = a \quad \text { if } \quad a \geq 0\)
Or more generally,
\(\sqrt { a ^ { 2 } } = | a | \quad \text { if } \quad a \in R\)
The absolute value is important because \(a\) may be a negative number and the radical sign denotes the principal square root. For example,
Make use of the absolute value to ensure a positive result.
Simplify: \(\sqrt { ( x - 2 ) ^ { 2 } }\).
- Answer
-
\(| x - 2 |\)
The importance of the use of the absolute value in the previous example is apparent when we evaluate using values that make the radicand negative. For example, when \(x = 1\),
Next, consider the square root of a negative number. To determine the square root of \(−25\), you must find a number that when squared results in \(−25\). However, any real number squared always results in a positive number. The square root of a negative number is requires complex numbers where \(i=\sqrt{-1}\). In this case the answer is \(\pm 5 i\) which is an imaginary number. As such, \(\sqrt { - 25 }\) is not a real number. Therefore, the square root function4 given by \(f ( x ) = \sqrt { x }\) is not defined to be a real number if the \(x\)-values are negative. The smallest value in the domain is zero. For example,\(f ( 0 ) = \sqrt { 0 } = 0\) and \(f ( 4 ) = \sqrt { 4 } = 2\). Recall the graph of the square root function.

The domain and range both consist of real numbers greater than or equal to zero: \([0, ∞)\). To determine the domain of a function involving a square root we look at the radicand and find the values that produce nonnegative results.
Example \(\PageIndex{3}\):
Determine the domain of the function defined by \(f ( x ) = \sqrt { 2 x + 3 }\).
Solution
Here the radicand is \(2x + 3\). This expression must be zero or positive. In other words,
\(2 x + 3 \geq 0\)
Solve for \(x\).
- Answer
-
Domain: \(\left[ - \frac { 3 } { 2 } , \infty \right)\)
A cube root5 of a number is a number that when multiplied by itself three times yields the original number. Furthermore, we denote a cube root using the symbol \(\sqrt [ 3 ] { }\), where \(3\) is called the index6. For example,
\(\sqrt [ 3 ] { 64 } = 4 , \text { because } 4 ^ { 3 } = 64\)
The product of three equal factors will be positive if the factor is positive and negative if the factor is negative. For this reason, any real number will have only one real cube root. Hence the technicalities associated with the principal root do not apply. For example,
\(\sqrt [3] {-64} = - 4 , \text { because } ( - 4 ) ^ { 3 } = - 64\)\)
In general, given any real number \(a\), we have the following property:
\(\sqrt [ 3 ] { a ^ { 3 } } = a \quad \text { if } \quad a \in R\)
When simplifying cube roots, look for factors that are perfect cubes.
Example \(\PageIndex{4}\):
Evaluate.
- \(\sqrt [ 3 ] { 8 }\)
- \(\sqrt [ 3 ] { 0 }\)
- \(\sqrt [ 3 ] { \frac { 1 } { 27 } }\)
- \(\sqrt [ 3 ] { - 1 }\)
- \(\sqrt [ 3 ] { - 125 }\)
Solution
- \(\sqrt [ 3 ] { 8 } = \sqrt [ 3 ] { 2 ^ { 3 } } = 2\)
- \(\sqrt [ 3 ] { 0 } = \sqrt [ 3 ] { 0 ^ { 3 } } = 0\)
- \(\sqrt [ 3 ] { \frac { 1 } { 27 } } = \sqrt [ 3 ] { \left( \frac { 1 } { 3 } \right) ^ { 3 } } = \frac { 1 } { 3 }\)
- \(\sqrt [ 3 ] { - 1 } = \sqrt [ 3 ] { ( - 1 ) ^ { 3 } } = - 1\)
- \(\sqrt [ 3 ] { - 125 } = \sqrt [ 3 ] { ( - 5 ) ^ { 3 } } = - 5\)
It may be the case that the radicand is not a perfect square or cube. If an integer is not a perfect power of the index, then its root will be irrational. For example, \(\sqrt [ 3 ] { 2 }\) is an irrational number that can be approximated on most calculators using the root button \(\sqrt [ x ] { }\).Depending on the calculator, we typically type in the index prior to pushing the button and then the radicand as follows:
\(3 \quad\sqrt [ x ] {y }\quad2\quad=\)
Therefore, we have
\(\sqrt [ 3 ] { 2 } \approx 1.260 , \quad \text { because } \quad 1.260 ^{\wedge} 3 \approx 2\)
Since cube roots can be negative, zero, or positive we do not make use of any absolute values.
Since the cube root of a function could be either negative or positive, we conclude that the domain consists of all real numbers. Sketch the graph by plotting points. Choose some positive and negative values for \(x\), as well as zero, and then calculate the corresponding \(y\)-values.
| \(x\) | \(f(x)\) | \(f ( x ) = \sqrt [ 3 ] { x }\) | \(\color{Cerulean}{Ordered\:Pairs}\) |
|---|---|---|---|
| \(-8\) | \(\color{Cerulean}{-2}\) | \((-8,-2)\) | |
| \(-1\) | \(\color{Cerulean}{-1}\) | \((-1,-1)\) | |
| \(0\) | \(\color{Cerulean}{0}\) | \(f ( 0 ) = \sqrt [ 3 ] { 0 } = 0\) | \((0,0)\) |
| \(1\) | \(\color{Cerulean}{1}\) | \(f ( 1 ) = \sqrt [ 3 ] { 1 } = 1\) | \((1,1)\) |
| \(8\) | \(\color{Cerulean}{2}\) | \(f ( 8 ) = \sqrt [ 3 ] { 8 } = 2\) | \((8,2)\) |
Plot the points and sketch the graph of the cube root function.
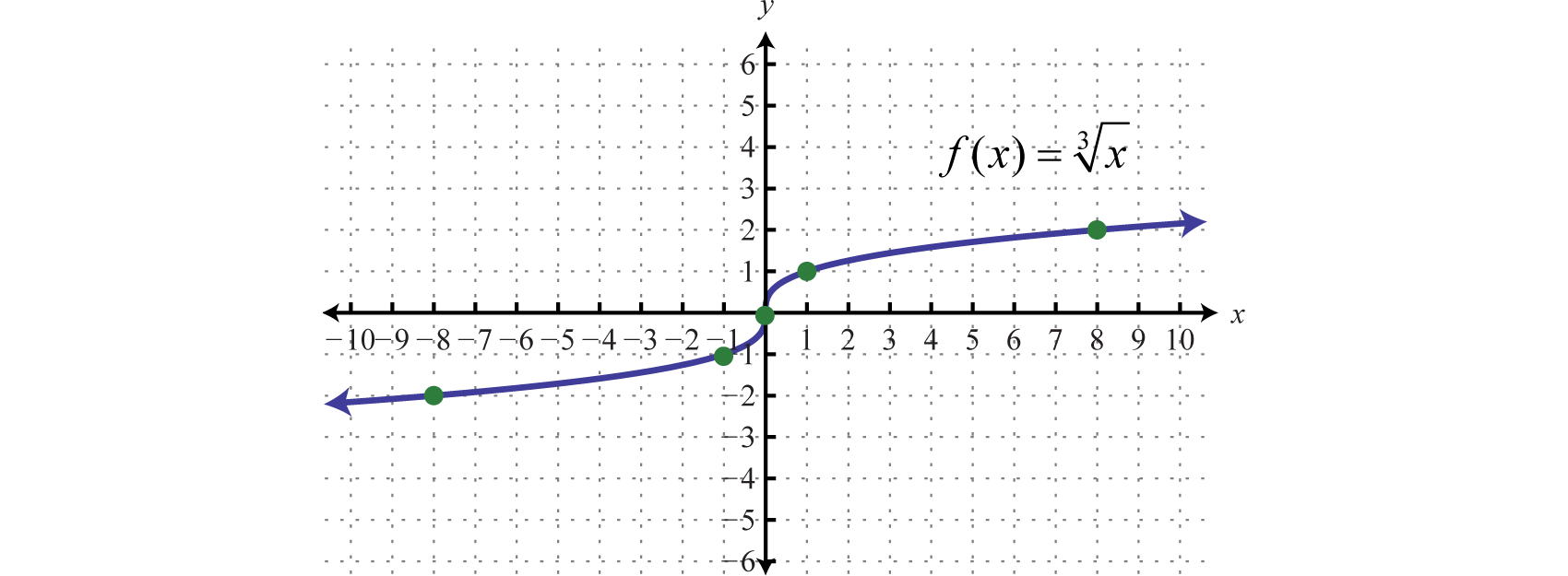
Figure \(\PageIndex{2}\): Graph of cube root of x
The graph passes the vertical line test and is indeed a function. In addition, the range consists of all real numbers.
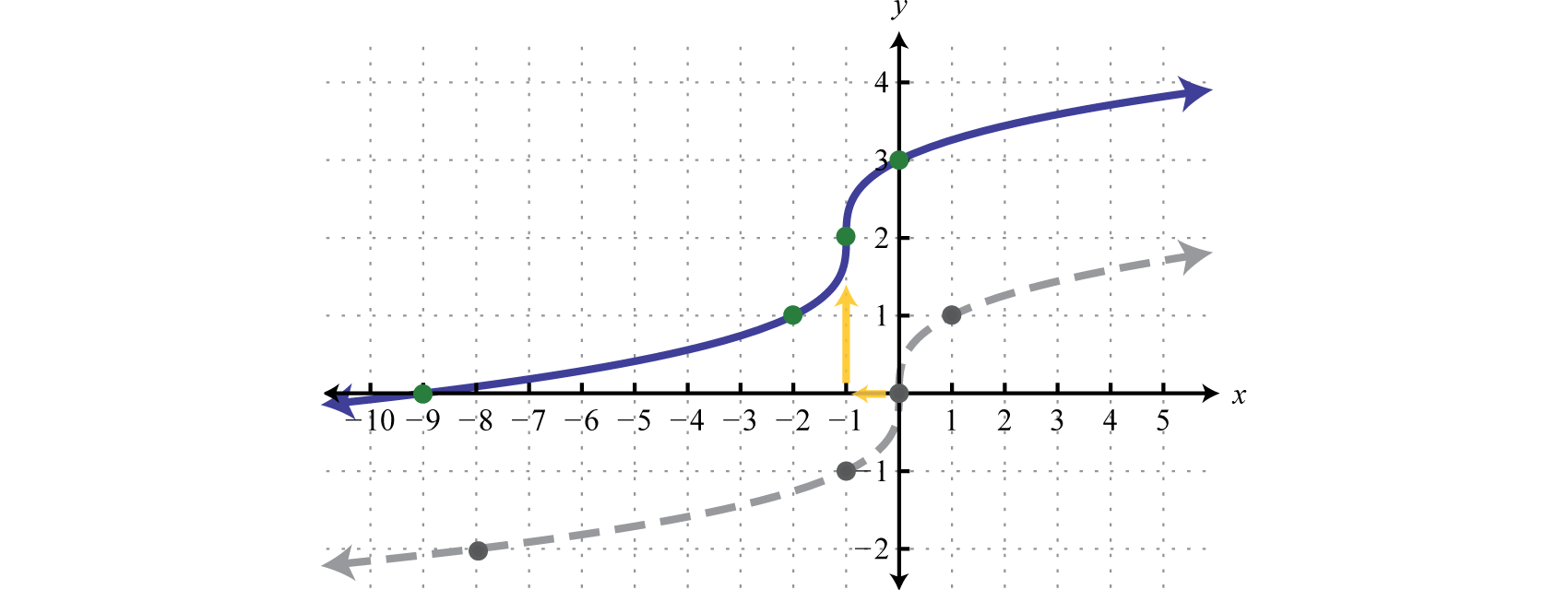
Example \(\PageIndex{5}\):
Given \(g ( x ) = \sqrt [ 3 ] { x + 1 } + 2\), find \(g ( - 9 ) , g ( - 2 ) , g ( - 1 )\), and \(g(0)\). Sketch the graph of \(g\).
Solution
Replace \(x\) with the given values.
| \(x\) | \(g(x)\) | \(g ( x ) = \sqrt [ 3 ] { x + 1 } + 2\) | \(\color{Cerulean}{Ordered\:Pairs}\) |
|---|---|---|---|
| \(-9\) | \(\color{Cerulean}{0}\) | \((-9,0)\) | |
| \(-2\) | \(\color{Cerulean}{1}\) | \((-2,1)\) | |
| \(-1\) | \(\color{Cerulean}{2}\) | \((-1,2)\) | |
| \(0\) | \(\color{Cerulean}{3}\) | \(g ( \color{OliveGreen}{0}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{0}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 1 } + 2 = 1 + 2 = 3\) | \((0,3)\) |
We can also sketch the graph using the following translations:
\(\begin{array} { l } { y = \sqrt [ 3 ] { x } \quad\quad\quad\quad \color{Cerulean} { Basic\: cube \:root\: function } } \\ { y = \sqrt [ 3 ] { x + 1 } \quad \quad\:\color{Cerulean} { Horizontal\: shift\: left\: 1\: unit } } \\ { y = \sqrt [ 3 ] { x + 1 } + 2 \:\:\:\color{Cerulean} { Vertical\: shift\: up\: 2\: units } } \end{array}\)
Answer:
nth Roots
For any integer \(n ≥ 2\), we define an nth root7 of a positive real number as a number that when raised to the nth power yields the original number. Given any nonnegative real number \(a\), we have the following property:
\(\sqrt [ n ] { a ^ { n } } = a , \quad \text { if } \quad a \geq 0\)
Here n is called the index and \(a^{n}\) is called the radicand. Furthermore, we can refer to the entire expression \(\sqrt [ n ] { A }\) as a radical8. When the index is an integer greater than or equal to \(4\), we say “fourth root,” “fifth root,” and so on. The nth root of any number is apparent if we can write the radicand with an exponent equal to the index.
Example \(\PageIndex{7}\):
Simplify:
- \(\sqrt [ 4 ] { 81 }\)
- \(\sqrt [ 5 ] { 32 }\)
- \(\sqrt [ 7 ] { 1 }\)
- \(\sqrt [ 4 ] { \frac { 1 } { 16 } }\)
Solution
- \(\sqrt [ 4 ] { 81 } = \sqrt [ 4 ] { 3 ^ { 4 } } = 3\)
- \(\sqrt [ 5 ] { 32 } = \sqrt [ 5 ] { 2 ^ { 5 } } = 2\)
- \(\sqrt [ 7 ] { 1 } = \sqrt [ 7 ] { 1 ^ { 7 } } = 1\)
- \(\sqrt [ 4 ] { \frac { 1 } { 16 } } = \sqrt [ 4 ] { \left( \frac { 1 } { 2 } \right) ^ { 4 } } = \frac { 1 } { 2 }\)
Note
If the index is \(n = 2\), then the radical indicates a square root and it is customary to write the radical without the index; \(\sqrt [ 2 ] { a } = \sqrt { a }\).
Lastly, for any real number \(a\) we have,
\(\begin{aligned} \sqrt [ n ] { a^ { n } } & = | a | \color{Cerulean}\:\:\: { When \: n\: is\: even } \\ \sqrt [ n ] {a^ { n } } & = a \quad\: \color{Cerulean} { When \: n\: is\: odd } \end{aligned}\)
When n is odd, the nth root is positive or negative depending on the sign of the radicand.
\(\sqrt [ 3 ] {27} = { ( - 3 ) ^ { 3 } } = - 3 \)
When n is even, the nth root is positive or not real depending on the sign of the radicand.
Exercise \(\PageIndex{2}\)
Simplify: \(- 8 \sqrt [ 5 ] { - 32 }\).
- Answer
-
\(16\)
Simplifying Radicals
It will not always be the case that the radicand is a perfect power of the given index. If it is not, then we use the product rule for radicals10 and the quotient rule for radicals11to simplify them. Given real numbers \(\sqrt [ n ] { A }\) and \(\sqrt [ n ] { B }\),
| Product Rule for Radicals: | \(\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }\) |
|---|---|
| Quotient Rule for Radicals: | \(\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }\) |
A radical is simplified12 if it does not contain any factors that can be written as perfect powers of the index.
Example \(\PageIndex{10}\):
Simplify: \(\sqrt { 150 }\).
Solution
Here \(150\) can be written as \(2 \cdot 3 \cdot 5 ^ { 2 }\).
\(\begin{aligned} \sqrt { 150 } & = \sqrt { 2 \cdot 3 \cdot 5 ^ { 2 } }\quad\quad \color{Cerulean} { Apply\: the\: product \:rule\: for\: radicals.} \\ & = \sqrt { 2 \cdot 3 } \cdot \sqrt { 5 ^ { 2 } }\quad\: \color{Cerulean} { Simplify. } \\ & = \sqrt { 6 } \cdot 5 \\ & = 5 \sqrt { 6 } \end{aligned}\)
We can verify our answer on a calculator:
\(\sqrt { 150 } \approx 12.25 \quad\text { and }\quad 5 \sqrt { 6 } \approx 12.25\)
Also, it is worth noting that
\(12.25 ^ { 2 } \approx 150\)
Answer:
\(5 \sqrt { 6 }\)
Note
\(5 \sqrt { 6 }\) is the exact answer and \(12.25\) is an approximate answer. We present exact answers unless told otherwise.
Fractional exponents as radicals
A fractional exponent is equivalent to a radical with an index being the reciprocal of the exponent. For instance \( x^{\frac{1}{2}}\) is the same as \(\sqrt[2] x\). This notation is used as a convenience when there are other exponents in your formula. To summarize,
\[x^{\frac{1}{n}} = \sqrt[n] x\]
All rules of exponents apply as before. For instance \(({x^{\frac{1}{2}}})^4 = x^{({\frac{1}{2}})(4)} = x^2\).
1A number that when multiplied by itself yields the original number.
2The positive square root of a positive real number, denoted with the symbol \(√\).
3The expression \(A\) within a radical sign, \(\sqrt [ n ] { A }\).
4The function defined by \(f ( x ) = \sqrt { x }\).
5A number that when used as a factor with itself three times yields the original number, denoted with the symbol \(\sqrt [ 3 ] { }\).
6The positive integer n in the notation \(\sqrt [ n ] { }\) that is used to indicate an nth root.
7A number that when raised to the \(n\)th power \((n ≥ 2)\) yields the original number.
8Used when referring to an expression of the form \(\sqrt [ n ] { A }\).
9The positive nth root when \(n\) is even.
10Given real numbers \(\sqrt [ n ] { A }\) and \(\sqrt [ n ] { B }\),\(\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }\).
11Given real numbers \(\sqrt [ n ] { A }\) and \(\sqrt [ n ] { B }\),\(\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }\) where \(B ≠ 0\).
12A radical where the radicand does not consist of any factors that can be written as perfect powers of the index.

