14.10.1: First-order Differential Equations
- Page ID
- 67370
General first-order differential equation
We consider the general first-order differential equation:
\[\tau \frac{d y(t)}{d t}+y(t)=x(t)\]
The general solution is given by:
\[y(t)=y_{0} e^{-\left(t-t_{0}\right) / \tau}+\frac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{\left(t^{\prime}-t_{0}\right) / \tau} d t^{\prime}\]
where \(y_{0}=y \left(t-t_{0}\right)\). Note that \(t^{\prime}\) is used to be distinguished from the upper limit \(t\) of the integral.
To obtain the general solution, begin with the first order differential equation:
\[\tau \frac{d y(t)}{d t}+y(t)=x(t)\]
Divide both sides by \(\tau\):
\[\frac{d y(t)}{d t}+\frac{1}{\tau} y(t)=\frac{1}{\tau} x(t)\]
Rewriting in condensed form using the integrating factor \(e^{-\frac{t}{\tau}}\):
\[e^{-\frac{t}{\tau}} \dfrac{d}{dt}\left[e^{\frac{t}{\tau}} y(t) \right] = \dfrac{1}{\tau} x(t)\]
Notice how a chain differentiation will returns to previous form
Simplify:
\[\frac{d}{d t}\left[e^{t / \tau} y(t)\right]=\frac{1}{\tau} x(t) e^{t / \tau}\]
Integrate both sides:
\[e^{t / \tau} y(t)-e^{t_{0} / \tau} y\left(t_{0}\right)=\frac{1}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{t^{\prime} / \tau} d t^{\prime}\]
Solve for y(t):
\[y(t)=y_{0} e^{-\left(t-t_{0}\right) / \tau}+\frac{e^{-t / \tau}}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{t^{\prime} / \tau} d t^{\prime}\]
Example \(\PageIndex{1}\): Solutions of First Order Differential Equations
Consider:
\[\frac{d y(t)}{d t}=x(t)\]
Multiplying both sides by dt gives:
\[\int_{t_{0}}^{t} \frac{d y d t}{d t}=\int_{t_{0}}^{t} x\left(t^{\prime}\right) d t^{\prime}\]
The general solution is given as:
\[y(t)=y_{0}+\int_{t_{0}}^{t} x\left(t^{\prime}\right) d t^{\prime}\]
Now Consider:
\[\frac{d y(t)}{d t}=-a y(t)\]
Dividing both sides by y(t) gives:
\[\frac{1}{y(t)} \frac{d y(t)}{d t}=-a\]
which can be rewritten as:
\[\frac{d}{d t}[\ln (y(t))]=-a\]
Multiplying both sides by dt, integrating, and setting both sides of the equation as exponents to the exponential function gives the general solution:
\[y(t)=y_{0} e^{-a\left(t-t_{0}\right)}\]
Now Consider:
\[\frac{d y(t)}{d t}=-a y(t)+x(t)\]
The detailed solution steps are as follows:
1. Separate y(t) and x(t) terms
\[\frac{d y(t)}{d t}+a y(t)=x(t)\]
2. Rewrite the left hand side in condensed form using the "integrating factor" \(e^{-at}\)
\[e^{-at} \frac{d\left(e^{a t} y(t)\right)}{d t}=x(t)\]
Notice how a chain differentiation will return the LHS to the form written in step 1
3. Divide both sides by \(e^{-at}\)
\[\frac{d\left(e^{a t} y(t)\right)}{d t}=e^{a t} x(t)\]
4. Multiply both sides by dt and integrate
\[e^{a t} y(t)-e^{a t_{0}} y_{0}=\int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{a t^{\prime}} d t^{\prime}\]
The general solution is given as:
\[y(t)=y_{0} e^{-a\left(t-t_{0}\right)}+e^{-a t} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{a\left(t^{\prime}-t_{0}\right)} d t^{\prime}\]
Step Function Simplification
\[\tau \frac{d y(t)}{d t}+y(t)=x(t)\]
Using the step function we set \(x(t) = \Theta(t-t_0)\) and also set \(y_0 = 0\)
The step function is \(x(t)=1\) for \(t \ge t_0\) and \(x(t)=0\) otherwise:
The previously derived general solution:
\[y(t)=y_{0} e^{-\left(t-t_{0}\right) / \tau}+\frac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{\left(t^{\prime}-t_{0}\right) / \tau} d t^{\prime}\]
\[y(t)=\frac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \int_{t_{0}}^{t} \Theta(t-t_0) e^{\left(t^{\prime}-t_{0}\right) / \tau} d t^{\prime}\]
\[y(t)=\frac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \int_{t_{0}}^{t} e^{\left(t^{\prime}-t_{0}\right) / \tau} d t^{\prime}\]
\[y(t)=\frac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \left( \tau \left[e^{-\left(t^{\prime}-t_{0}\right) / \tau}\right] \right) \Biggr|_{t_0}^t\]
\[y(t)=\frac{e^{-\left(t-t_{0}\right) / \tau}}{\tau} \left( \tau \left[e^{-\left(t-t_{0}\right) / \tau} - 1\right] \right)\]
\[y(t)=\left(\left[e^{-2\left(t-t_{0}\right) / \tau} - e^{-\left(t-t_{0}\right) / \tau}\right] \right)\]
\[y(t)=e^{-\frac{(t-t_0)}{\tau}}\]
The quantity \(\tau\) is a time constant that reflects when \(y(t)\) drops to \(\frac{1}{e}\) of its original value.
Example \(\PageIndex{2}\)
Problem Statement:
Consider the differential equation
\[\frac{d y(t)}{d t}=-0.5 y(t)+x(t)\]
where \(x(t) = 2 + 0.01t\)
Assuming \(y_0 = 0\), what is the behavior of \(y(t)\)?
Solution
General solution was derived previously as:
\[y(t)=y_{0} e^{-a\left(t-t_{0}\right)}+e^{-a t} \int_{t_{0}}^{t} x\left(t^{\prime}\right) e^{a\left(t^{\prime}-t_{0}\right)} d t^{\prime}\]
For \(a=0.05\) and \(y_0=0\), while setting \(t_0 = 0\), the solution reduces to:
\[y(t)=e^{-0.5 t} \int_{0}^{t}\left(2+0.01 t^{\prime}\right) e^{0.5\left(t^{\prime}\right)} d t^{\prime}\]
Using the integral table in this chapter and simplifying gives the following:
\[y(t)=\frac{\left.\left(e^{-0.5 t}\right)\left((x+198)\left(e^{0.5 t}\right)-198\right)\right)}{50}\]
Plotting this function displays the following behavior:
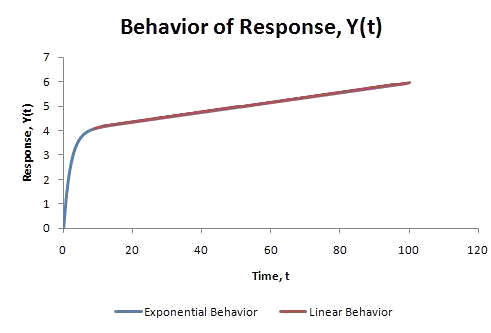
As can be seen clearly from the graph, initially the systemic response shows more exponential characteristics. However, as time progresses, linear behavior dominates.
Parachute Person
If you remember in the section on parachute person we developed a first order differential equation.
\[ \frac{dv}{dt} + \dfrac{c}{m} v^2 = g\]
This is a form of a Riccate1 differential equation, albeit a simple one. It is solvable2 but requires a known particular solution (which we could assume easily given that g is a constant), however it is easier to solve this just with an Euler approximation as was done in the parachute person section. Furthermore, this problem becomes more complex as you add more real world components to it, up to and including the addition of Navier-Stokes equation3. So a numerical approximation is the better method to follow for parachute person and is worth learning.
1Which is known for leading to a differential equation solution to the time independent Schrödinger equation, not parachute person.
2If we write the equation in the form \(\frac{dv}{dt} = \left(\sqrt{\frac{m}{c}g}\right)^2 - v^2\) and then rewrite so we can integrate as \(\frac{m}{c}\frac{dv}{\left(\sqrt{\frac{m}{c}g}\right)^2 - v^2} = dt\). This will eventually lead to a solution (with some assumptions and an integral table): \(v = \sqrt{\left(\frac{m}{c}g\right)} \tanh{\left(g\sqrt{\frac{c}{m}}t\right)}\).
3The Navier-Stokes equation is for fluid motion. Air is considered a fluid. Navier-Stokes will be discussed later in this course/book, but only briefly as this is a higher level subject.


