Metallic Reflection

When a light beam encounters a material, radiation can be absorbed or reflected by the surface. Metals are known for having high reflectivity, which explains their shiny appearance. Since the reflectance of light by metals is high their absorption is low because the sum of both must correspond to 100% of the incident light. Since absorptivity equals emissivity by Kirkhoff's Law, that is also low for metals. The absorption of light can happen due to lattice vibrations and excitation of electrons to higher energy levels. Also, high reflectance of light in lower frequencies is associated with high conductivity of the metal, according to Hagens-Ruben relation.

Absorption Phenomena

If a light beam of certain wavelength is focused on a metal, the radiation is attenuated due to energy loss from lattice vibrations (heat) and excitation of electrons from the valence band to conduction band. In metals, there is an overlap between valence band and conduction band or a partially-filled valence band, which leads to conduction of electrons to energy levels above the Fermi level. This phenomena is shown in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Scheme of the absorption of light by a metal, occurring lattice vibrations (a) and electron promotion to higher energy levels (b).

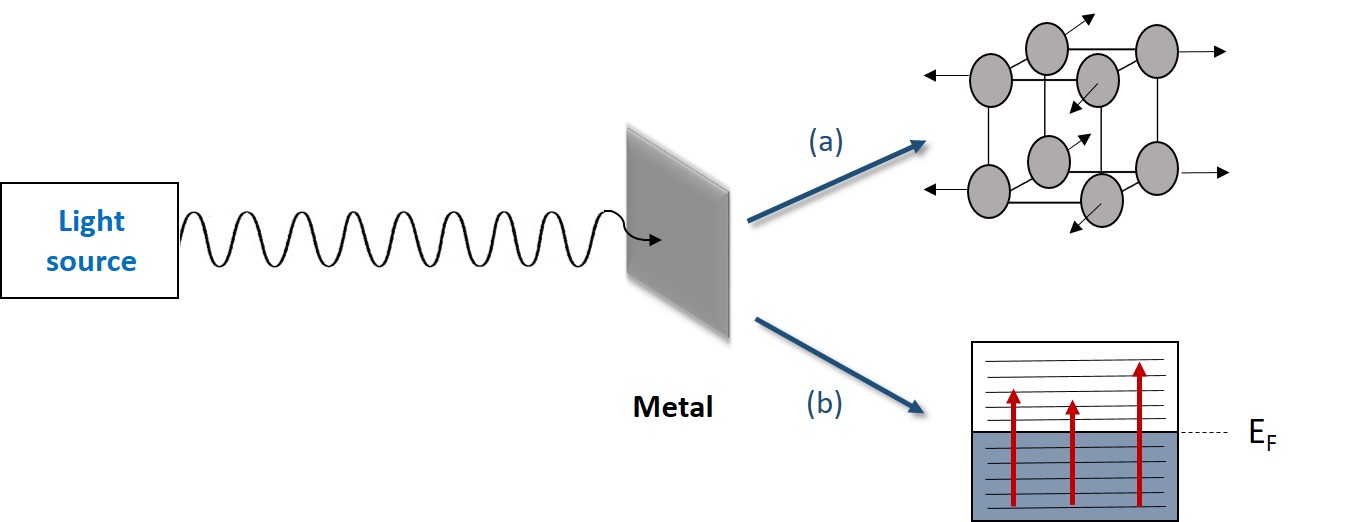
When electromagnetic radiation encounters the metallic surface, the intensity of the incident light (I₀) decreases exponentially while it travels through the metal, leading to a transmitted light (I) of lower intensity ( Figure \(\PageIndex{2}\)). This happens because metals can damp the initial intensity of light (I₀), and the decrease of light intensity is related to thickness of the metal (z), the incident wavelength, and the damping constant (k), or extinction coefficient. Where k describes the efficacy of a metal for light damping. This relationship is shown in Equation \ref{1}.

Figure \(\PageIndex{2}\): Scheme of the initial intensity of light (I0) changing to transmitted intensity (I) when the radiation passes through a metal with thickness (z).

\[I=I_0 \exp(\frac{-4 \pi k z}{\lambda} \label{1})\]

The ratio between the transmitted intensity (I) and the initial intensity (I₀) is defined as transmittance (T), shown in Equation \ref{2}.

\[T=\frac{I}{I_0} \label{2}\]

Also, the change in light intensity is related to the penetration depth (W), which is the distance required for the intensity of light (I₀) to be diminished to 1/e or 37% of its initial value. The reciprocal of the penetration depth is defined as absorbance (α), which is the amount of energy absorbed by the metal when radiation passes through (Equation \ref{3}).

\[W=\frac{1}{\alpha}=\frac{\lambda}{4 \pi k} \label{3}\]

Metallic Reflection

Metals have high reflectivity, reflecting almost all wavelengths in the visible region of the spectrum. This is related to their high damping constant, which leads to a short distance crossed by the light. In addition, some metals have low refractive index and, according to Snell's Law, when light passes through a medium of higher refractive index to a medium of low refractive index, the refracted ray will have a large deflection in relation to the normal. This features explain the behavior of some metals such as silver, gold and copper towards incidence of electromagnetic radiation. A schematic representation of this process is shown in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): Reflectance phenomena where the incidence of light in metal leads to metallic reflection (a) and light attenuation or absorption (b).

Therefore, the Reflectance (R) of a material can be defined as the efficiency of a material to reflect incident light. This value depends only on the complex refractive index (n) and the damping constant (k), which is shown in Equation \ref{4}.

\[R=\frac{(n-1)^2+k^2}{(n+1)^2+k^2} \label{4}\]

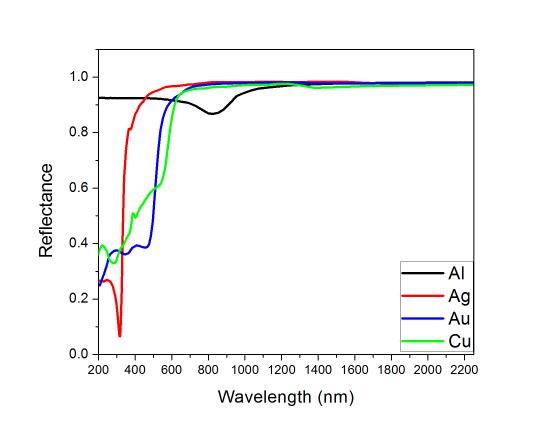
The study of metallic reflectance can be applied on metallic coatings, which is expected that the metal reflect light in a wide range of wavelengths. Also, it can explain the colors displayed by the metals. Silver, for instance, has high reflectivity over the visible range of the spectrum, which makes it colorless when white light is focused on the metal. Gold, however, absorbs the blue and violet regions of the spectrum, leading to a yellow color when illuminated with white light. The reflectance spectra of silver, gold, copper and aluminum is represented in Figure \(\PageIndex{4}\), where it can be observed that those metals have high reflectance in a wide range of wavelengths, specially in the visible region of the spectrum. However, if the frequency is large (lower wavelength values), silver, copper and gold have a drop in reflectance.

Figure \(\PageIndex{4}\): Reflectance spectra of the metals: aluminum(black line), silver(red line), gold(blue line) and copper(green line).

Reflectance and conductivity

The metallic reflectance can be related to the conductivity by the Hagens-Ruben equation (Equation \ref{5}), where ν is the light frequency, ε₀ is the vacuum permitivity (8.85 x 10^-12 F/m), and σ is the conductivity. In the infrared region (small frequencies), this equation shows that metals with high reflectance also are good conductors.

\[R=1-4 \sqrt{\frac{\nu \pi \epsilon_0} {\sigma}} \label{5}\]

This conclusion was derived by Drude and confirmed experimentally by Hagens-Ruben. It was observed that, at higher wavelengths (lower frequencies), the optical constants of metals are similar to the values of Drude`s function, where the complex refractive index is much smaller then the damping constant, or extinction coefficient. This leads to high reflectance. However, in higher frequencies, deviations of Drude`s approach start to appear, because bound electrons of the metal start to respond to the incidence of light, instead of just valence band electrons response. This leads to a decrease in reflectivity, which depends on the metal's characteristics.

Questions

1. A light of 632.8 nm is focused on a gold sample of damping constant (k) of 3.068. Calculate the penetration depth and absorbance of the sample.
2. A silver sample has complex refractive index and damping constant equal to 0.135 and 3.985, respectively, when a light of 632.8 nm (ν = 4.74 x 10¹⁴ Hz) is focused on the sample. Calculate the reflectance (R) for this sample.
3. With the value of reflectance obtained in Question 2, calculate the expected conductivity for silver.

Answers

1. W=16.4 nm and α= 0.061 nm^-1.
2. R=0.968 (96.8%).
3. \(2.06 \times 10^8\, Ω^{-1}m^{-1}\).

References

1. Kasap, S. O. Principles of Electronic Materials and Devices. McGraw-Hill. 3^rd edition. 2006.
2. Stenzel, O.. The physics of thin film optical spectra: an introduction. Springer. 2015.
3. Hummel, R. E.. Electronic Properties of Materials. Springer. 3^rd edition. 2001.
4. Kortum, G.. Reflectance spectroscopy: Principles, Methods, Applications. Springer. 2012.
5. Quinn, J. J., Yi, K.. Solid State Physics: Principles and Modern Applications. Springer. 2009.
6. Dressel, M., Scheffler, M.. Verifying the Drude response. Ann. Phys. v. 15. 2006.

Contributors and Attributions

• Andressa Dancini Goncalves - (Materials Science and Engineering - UC Davis)