4.6: Defects

Within a single crystal or grain, the crystal structure is not perfect. The structure contains defects such as vacancies , where an atom is missing altogether, and dislocations , where the perfection of the structure is disrupted along a line. Grain boundaries in polycrystals can be considered as two-dimensional defects in the perfect crystal lattice. Crystal defects are important in determining many material properties, such as the rate of atomic diffusion and mechanical strength.

We can use a "shot model" to get a picture of crystal defects. The model consists of many small ball bearings trapped in a single layer between two transparent plates. They tend to behave like the atoms in a crystal, and can show the same kind of defects.

When the shot model is held horizontally, so that the balls flow freely, the resulting structure is similar to a liquid.

Shot model held horizontally. The balls form a liquid-like structure.

As the model is tilted towards the vertical, the balls pack closely together. This represents crystallisation. One or two balls may be suspended above the main body by electrostatic forces: this is comparable to the vapour found above the crystal.

In some places the balls form close-packed regions. Tapping of the model causes minor rearrangements of the balls, especially at the top of the "solid" region. This is similar to diffusion, in which case the tapping is analogous to thermal activation. Occasionally, the "diffusion" process may cause two grains to join together, or for some grains to "grow". The following image sequence shows the behaviour of the shot model as it is rearranged by tapping, starting from a polycrystalline state with many small grains and ending with much larger grains. Note the presence of vacancies in the structure.

https://www.doitpoms.ac.uk/tlplib/at...rainGrowth.mp4

Grain growth in the shot model

With great care, it may be possible to create a single crystal, as all the balls form a single pattern. Note that diffusion occurs mainly near the top of the balls: those towards the middle and bottom do not easily move, as the photographs show.

Even in a single crystal, or large-grained sample, there are still vacancies, as the shot model shows. The reason for this involves entropy: at all finite temperatures, there will be some disorder in the crystal.

The balls within a grain arrange themselves into close-packed planes. In metals, close-packing of atoms is a very common structure. This pattern is typical of hexagonal close-packed and cubic close-packed lattices. Note that in this 2-D model, each ball touches six others. In a 3-D crystal, such as a real one, each ball would also touch three on the plane above, and three on the plane below.

A close-packed plane.

In the shot model, the balls are normally arranged in to a polycrystalline form, shown schematically below:

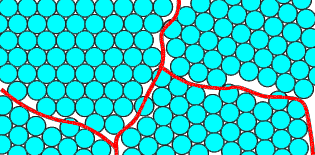
A polycrystal will typically have crystalline regions (grains) bounded by disordered grain boundaries. These boundaries are marked in the picture on the right.

Note that the packing of atoms at the grain boundaries is disordered compared to the grains. At a grain boundary, the normal crystal structure is obviously disturbed, so the boundaries are regions of high energy. The ideal low energy state would be a single crystal.

Polycrystals form from a melt because crystallisation starts from a number of centres or nuclei . These developing crystals grow until they meet. Since they are not usually aligned before meeting, the grains need not necessarily be able to fit together as a single crystal, hence the polycrystalline structure.

After crystallisation the solid tends to reduce the boundary area, and hence the internal energy, by grain growth. This can only happen by a process of atomic diffusion within the solid. Such diffusion is more rapid at a higher temperature since it is thermally activated .