18.11: Applications of Dielectrics

A major use of dielectrics is in fabricating capacitors. These have many uses including storage of energy in the electric field between the plates, filtering out noise from signals as part of a resonant circuit, and supplying a burst of power to another component. The TLP on ferroelectrics shows how the last of these functions is utilised in a camera flash system.

The larger the dielectric constant, the more charge the capacitor can store in a given field, therefore ceramics with non-centrosymmetric structures, such as the titanates of group 2 metals, are commonly used. In practice, the material in a capacitor is in fact often a mixture of several such ceramics. This is due to the variation of the dielectric constant with temperature discussed earlier. It is generally desirable for the capacitance to be relatively independent of temperature; therefore modern capacitors combine several materials with different temperature dependences, resulting in a capacitance that shows only small, approximately linear temperature-related variations.

Of course in some cases a low dielectric loss is more important than a high capacitance, and therefore materials with lower values of κ – and correspondingly lower dielectric losses – may be used for these situations.

Some applications of dielectrics rely on their electrically insulating properties rather than ability to store charge, so high electrical resistivity and low dielectric loss are the most desirable properties here. The most obvious of these uses is insulation for wires, cables etc., but there are also applications in sensor devices. For example, it is possible to make a type of strain gauge by evaporating a small amount of metal onto the surface of a thin sheet of dielectric material.

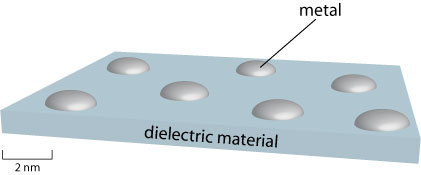
Electrons may travel across the metal by normal conduction, and through the intervening dielectric material by a phenomenon known as quantum tunnelling. A mathematical treatment of this phenomenon is outside the scope of this TLP; simply note that it allows particles to travel between two “permitted” regions that are separated by a “forbidden” region and that the extent to which tunnelling occurs decreases sharply as distance between the permitted regions increases. In this case the permitted regions are the solidified metal droplets, and the forbidden region is the high-resistance dielectric material.

If the dielectric material is strained, it will bow causing the distances between the metal islands to change. This has a large impact on the extent to which electrons can tunnel between the islands, and thus a large change in current is observed. Therefore the above device makes an effective strain gauge.