21.10: Lattice Resistance

Last updated
Save as PDF

Page ID: 31775

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The higher the Peierls stress the higher the lattice resistance. The model showed an exponential dependence of Peierls stress on w/b (and hence d/b since we found that was the key factor affecting dislocation width).This exponential dependence is very important and is seen in materials experimentally.

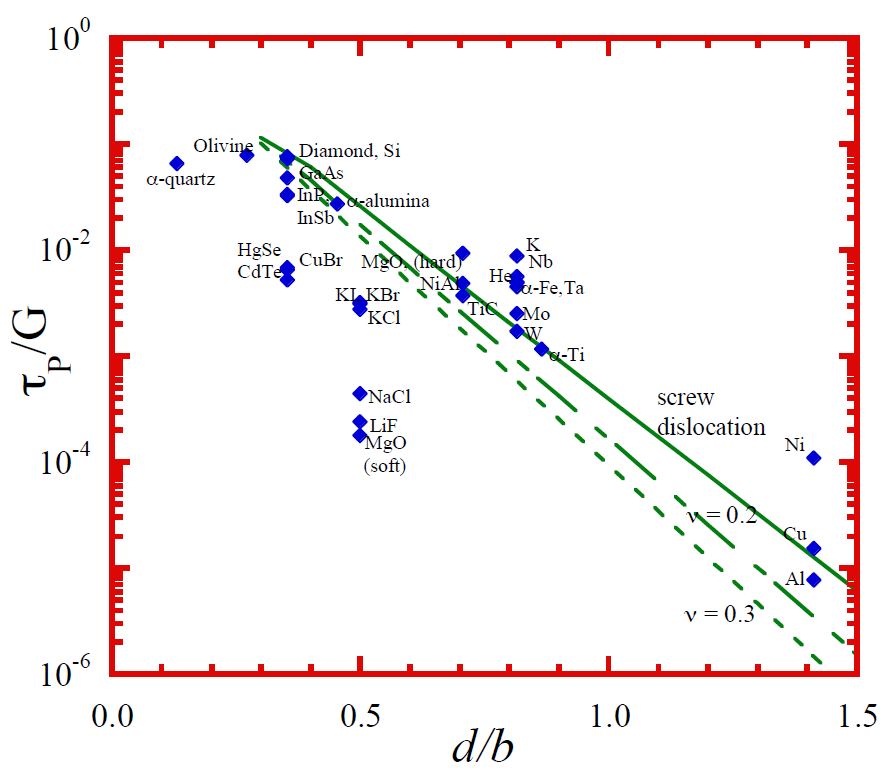
d over b versus tau graph

That τ_P can be predicted for both metallic and covalent materials using the atomistic model; there is no obvious effect of bonding. d/b is the important factor. We often think of covalent materials as the "strongest", but this graph shows otherwise. Experimental determination of the Peierls stress is done by considering the yield stress at zero kelvin. It is seen that the materials tend to follow the trend for giant covalent crystals (diamond, TiC); but it is more complicated when there are coulombic forces coming in to play, for example in ionic crystals.

It is important to consider what slip system we are using. For example, halides (NaCl, LiF) and MgO have two slip systems – {100} <110> (for which there is good agreement) and {110} <110> (for which the model predicts too high a Peierls stress by ≈10²).