22.9: Questions

Quick questions

You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

Which of the following statements is false?

a	A bubble raft can demonstrate vacancies and solute atom defects.
b	Plastic deformation in a bubble raft occurs by dislocation motion.
c	Screw dislocations can be seen in the bubble raft.
d	Bubbles in a well-formed bubble raft are close-packed.

Answer

C

Which of the following statements best describes the nature of dislocations in an amorphous material?

a	Amorphous materials cannot contain dislocations.
b	The dislocation density in an amorphous material is normally less than the dislocation density in a crystalline material with the same composition.
c	The dislocation density in an amorphous material is normally greater than the dislocation density in a crystalline material with the same composition.
d	A dislocation in an amorphous material must be of the edge type.

Answer

A

What are the conventional units of dislocation density?

a	m^-2
b	m^-3
c	kg m^-3
d	kg m^-2

Hint: Dislocation density is defined as the length of dislocation line per unit volume of material.

Answer

A

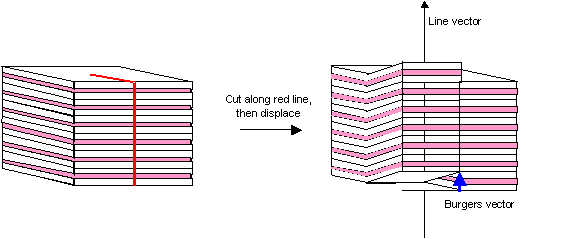
How would you make a stack of ham sandwiches look like a screw dislocation?

Hint: You need to make one cut in the stack, then displace the sandwiches on one side of the cut by a Burgers vector. What must the Burgers vector be?

Answer

The Burgers vector is one sandwich thickness. The cut is made halfway through the stack, as shown below. After displacement, one can follow the ham continuously along the 'screw'.

Deeper questions

The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

Do the explanations of these experimental observations involve the concept of dislocations? (Answer yes or no for each)

Yes	No	a	The yield stress of a material is lower than that calculated from assuming a perfect lattice
Yes	No	b	In some cases, the stress required to continue plastic deformation increases as deformation proceeds
Yes	No	c	The yield stress of most metals decreases as the temperature increases
Yes	No	d	Ceramics tend to be brittle, whereas metals tend to be ductile

Answer

A. Yes. Dislocations can move through a lattice under a significantly lower applied stress than would be required to cause slip in a perfect lattice. Plastic deformation therefore occurs by dislocation motion in the majority of circumstances. (Note that other mechanisms of plastic deformation may occur, such as diffusion creep and twinning).

B. Yes. This is the phenomenon of work hardening. The mechanisms of work hardening involve mobile dislocations interacting to form sessile dislocations that cannot move under an applied stress, and the creation of forest dislocations - these intersect other slip planes and act as obstacles to dislocation motion on those planes, raising the stress required for dislocation glide.

C. Yes. The yield stress is the stress at which the metal begins to plastically deform, and since plastic deformation occurs (in most cases) by dislocation motion, it can be deduced that the stress required to drive dislocations through the metal is temperature dependent. As the temperature is increased, dislocation climb becomes easier. Climb allows dislocations to move onto parallel slip planes in order to overcome obstacles, and hence the yield stress is temperature dependent. (The ability of dislocations to climb over obstacles at high temperatures determines a material's susceptibility to creep, i.e. plastic deformation at stresses below the yield stress.)

D. Yes. The width of a dislocation determines the stress required for glide. Narrow dislocations, commonly found in ceramics, require greater applied stress to glide than wide dislocations, which are often found in metals. The stress required for plastic flow in ceramics normally exceeds the stress needed to drive a crack through the material hence brittle fracture occurs. In ductile metals, plastic flow occurs before brittle fracture.

The energy per unit length, U, associated with an edge dislocation is given by

U ~ 0.5(Gb²)

where b is the magnitude of the Burgers vector b and G is the shear modulus. Estimate the energy per unit length of a dislocation in silver.

Data for silver: Crystal system is cubic F, a = 0.409 nm. b lies parallel to <110> directions. Shear modulus G = 28.8 GPa.

Answer

This question requires the magnitude of the Burgers vector to be calculated. The magnitude is the distance between adjacent lattice points in the direction of b. In the cubic crystal systems, the <110> directions lie along the face diagonals. In cubic F, there are lattice points at 0,0,0 and ½,½,0 (i.e. at the corners and face centres of the unit cell). The possible Burgers vectors can therefore be written as b = ½<110>. The magnitude of the Burgers vector can be deduced by considering the atoms on one face of the unit cell:

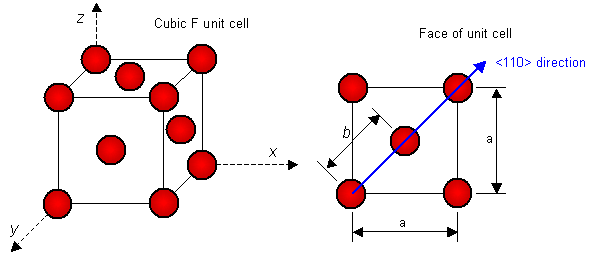
By geometry, the magnitude of the Burgers vector is b = a/2^1/2 = 0.289 nm. The energy of the dislocation per unit length of dislocation line is then

U = ½Gb² = ½ x 28.8 x 10⁹ x (0.289 x 10^-9) = 1.2 x 10^-9 J m^-1

Determine whether the following dislocations in sodium chloride are edge, screw or mixed. Identify the slip plane in which the dislocation lies. (Sodium chloride is cubic F and slips on {110} slip systems.)

	Burgers vector b parallel to:	Line vector l parallel to:
a	[110]	[110]
b	[001]	[110]
c	[100]	[111]

Hint: Edge dislocations have b perpendicular to l, screw dislocations have b parallel to l. Mixed dislocations have b at some acute angle to l. Determine the angle b^l using the scalar (dot) product or otherwise. Both b and l must lie in the slip plane of the dislocation. The is one method of determining whether a vector lies in a plane when both vector and plane are specified by Miller indices and the crystal system is cubic.

Answer

a) Screw (since b is parallel to l). Slip plane is (bar1 1 0), since this is the only allowed slip plane in which both b and l lie.

b) Edge (since b is perpendicular to l). Slip plane is (110), since this is the plane specified by the two vectors.

c) Mixed - the angle between b and l is cos^-1(1/3^½) = 54.7°. Slip plane is (0 bar1 1), since this is the plane specified by the two vectors.

Which of the following statements is true? (answer yes or no for each)

Yes	No	a	Using high-resolution microscopy techniques, it is possible to probe the structure of a dislocation.
Yes	No	b	The number of dislocations in a sample of material affects the ease of diffusion of impurities through the sample.
Yes	No	c	The diffusion of impurity atoms in a sample of a material affects the ease of motion of dislocations under an applied stress.

Answer

A. Yes. Modern transmission electron microscopy techniques have made it possible to create lattice images showing atoms in dislocations.

B. Yes. The atomic lattice is disrupted in the region of a dislocation - strain fields are present that make the lattice more 'open' or more 'closed' than the perfect structure. This can affect the diffusivity of species in the region of the dislocation. A sample of a material with a high dislocation density may exhibit higher diffusion coefficients for solutes than a sample of the same material with a lower dislocation density.

C. Yes.

Several effects are important:

• Dislocation motion is hindered by the presence of obstacles, such as precipitates of a second phase. The diffusivity of atoms making up this second phase affects the distribution and stability of precipitates, and hence affects the extent of precipitate strengthening.
• Dislocations can overcome obstacles like precipitates by climb, in which the dislocation moves through the structure onto other parallel slip planes until it can glide past the obstacle. Climb involves the diffusion of vacancies.
• Solution strengthened materials rely on the size difference between the host lattice atoms and substitutional solutes. The strain fields in the lattice around the solutes interact with the strain fields around dislocations, hindering dislocation motion. Diffusion is important in determining the distribution of these substitutional solutes and the ability of the dislocations to climb past them.
• Impurities can diffuse to the core of a dislocation, where the lattice is under dilatational strain (in the case of an edge dislocation). The dislocation is a sink for impurities. This build-up of solutes is called a Cottrell atmosphere. The presence of these impurities at the core makes it more difficult for the dislocation to move. This phenomenon is the origin of dynamic strain ageing (or the Portevin-Le Chatelier effect). Here, carbon diffusion to dislocation cores in mild steel occurs rapidly enough at elevated temperatures to cause 'jerky' plastic flow. Dislocations break free from their Cottrell atmospheres at some applied local stress, but can then glide at a lower applied local stress. If the dislocation motion slows or pauses, the Cottrell atmosphere around the dislocation core builds up again as carbon diffuses to the sink, and a higher stress must again be applied before glide can proceed.

Open-ended questions

The following questions are not provided with answers, but intended to provide food for thought and points for further discussion with other students and teachers.

9. Is dislocation glide always the mechanism of plastic flow? How might other mechanisms operate?
10. Why might the presence of dislocations in materials used for electronic components (such as integrated circuits) be a problem? How might the problem be reduced or solved?
11. Plastically deforming a material requires energy input. In what ways is this energy dissipated? Is any of it stored in the material?