Home
Bookshelves
Materials Science
TLP Library I
28: Ferroelectric Materials
28.7: Temperature Dependence of the Hysteresis Loop

28.7: Temperature Dependence of the Hysteresis Loop

Last updated
Save as PDF

Page ID: 32821

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We have now seen the way in which the hysteresis loop arises. However, there are more aspects to the hysteresis loop.

We have only observed it at one particular temperature, one at which the material is ferroelectric. What happens if the temperature is raised? The hysteresis loop changes with temperature, becoming sharper and thinner, and eventually disappearing, i.e.:

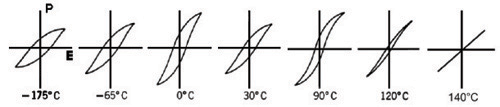
Hysteresis loops at different temperatures

As you can see, the polarisation increases at 90°C, as a result of a phase transition. Between this temperature and room temperature, the polarisation increases steadily, as a direct relation with temperature, such that:

ΔP = p ΔT

where p = pyroelectric coefficient (C m^-2T^-1).

Click here to find out more about pyroelectrics.

Why should this be?
This is a general behaviour (that does not apply to KNO₃) that can arise for two reasons depending on the material.

Disorder. Each unit cell has its own dipole moment, which, when there is a net polarisation, are described as ordered. At high T, the direction of the dipole moments randomises, giving a disordered material with no net polarisation.
Phase transitions that can open up new possibilities for dipole moments to form. In this case, there is a jump at 0°C, and at 90°C, where the loop becomes taller.