29.6: Domains

Domains are regions of a ferromagnetic material in which the magnetic dipole moments are aligned parallel. When the material is demagnetised the vector summation of all the dipole moments from all the domains equals zero. When the material is magnetised the vector summation of the dipoles gives an overall magnetic dipole (we will discuss this in more detail later).

Why do domains occur?

From our previous discussion of the exchange interaction it would appear that the most stable state would be that of a single domain where all the electron spins would be aligned parallel. However, while this minimises the energy contribution arising from the exchange interaction, there are other contributions to the total magnetic energy that must be considered:

• Magnetostatic energy
• Magnetostrictive energy
• Magnetocrystalline energy

We will now consider each in turn:

Magnetostatic energy

If a material consists of a single domain then it behaves as a block magnet (Figure L (i) below) and so a “demagnetising field” (the blue arrows) must be present around the block. This external, demagnetising field has a magnetostatic energy that depends on the shape of the sample and is the field that allows work to be done by the magnetised sample (e.g. lifting another ferromagnetic material against the force of gravity). In order to minimise the total magnetic energy the magnetostatic energy must be minimised. This can be achieved by decreasing the external demagnetising field by dividing the material into domains (Figure L (ii)). Adding extra domains increases the exchange energy, as the domains cannot align parallel, however the total energy has been decreased as the magnetostatic energy is the dominant effect. The magnetostatic energy can be reduced to zero by a domain structure that leaves no external demagnetising field (Figure L (iii)).

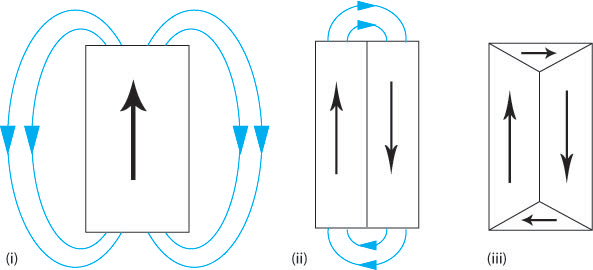
Figure L. Schematic showing how the addition of domains can reduce the external demagnetising field therefore reducing the magnetostatic energy.

This is the main driving force for the formation of domains.

Magnetocrystalline energy

Up until now, we have ignored the influence of the atomic lattice structure; however this also has an affect on the total energy of a magnetised sample. A ferromagnetic material has ‘easy’ crystallographic directions along which it is preferred that the magnetisation vector points and ‘hard’ directions along which a higher field is required to achieve the same magnetisation. Therefore, it is easiest to magnetise a ferromagnetic material along these easy axes, as shown by the schematic below.

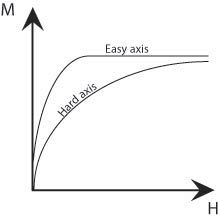
Figure M. Schematic showing the difference in size of field required to achieve the same magnetisation along easy and hard axes.

There is an energy difference associated with magnetisation along the hard and easy axes which is given by the difference in the areas under (M,H) curves. This is called the magnetocrystalline energy. This energy can be minimised by forming domains such that their magnetisations point along the easy crystallographic directions. The ideal material might have easy crystallographic directions perpendicular to one another as then both the magnetostatic and magnetocrystalline energies could both be minimised (Figure L (iii) above). In the regions bounding the domains, the domain walls, there must be a change in the direction of the magnetisation. Therefore, it cannot be aligned along easy axes and so large domains with few domain walls minimise the magnetocrystalline energy.

Below a table shows a summary of the easy, hard and intermediate directions in iron, nickel and cobalt:

	Fe	Ni	Co
	bcc	fcc	hexagonal
Easy	<100>	<111>	<1000>
Intermediate	<110>	<110>
Hard	<111>	<100>	<1010>

Magnetostrictive energy

When a ferromagnetic material is magnetised it changes length. This is known as magnetostriction; an increase in length along the direction of magnetisation is positive magnetostriction (e.g. in Fe), and a decrease in length is negative magnetostriction (e.g. in Ni). These length changes are usually extremely small; in the range of tens of parts per million. However, they do affect the domain structure of the material.

In iron the change in length causes the domains of closure to attempt to elongate horizontally (shown in blue in Figure N (i)) and the vertical domains to attempt to elongate vertically (shown in green in Figure N (i)). It is impossible for both to be accommodated and so this causes elastic strain in the material. The elastic strain energy is proportional to the volume of the domains of closure hence magnetostrictive energy can be minimised by decreasing the size of these domains. Reducing the volume of the domains of closure also requires the primary domains to decrease in size and increase in number (Figure N (ii)). The addition of extra domain walls increases the magnetocrystalline and exchange energy contributions to the total energy.

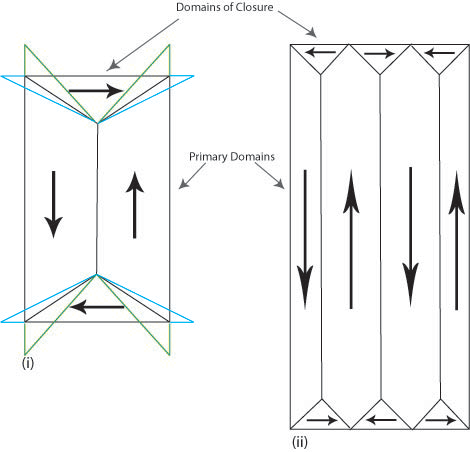
Figure N. Schematic showing the attempted change in shape of the domains (i) and the actual change (ii) due to magnetostriction.

The actual domain structure is a compromise of all the aforementioned energy contributions.