17.2: Powder Particles in a Fluid Stream
- Page ID
- 8277
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Particles in a fluid can experience several different types of force. The main ones are: (a) Gravitational / Buoyancy (usually due to the particle being more dense than the fluid, creating a force in the direction of a gravitational, or centrifugal, acceleration), (b) Drag (Viscous) (a velocity difference between particle and fluid leading to a drag force acting to reduce this difference) and (c) Electrostatic (due to particles becoming electrically charged and experiencing forces if electric or magnetic fields are present).
A key characteristic of fluid flows is the Reynolds number, Re, representing the ratio of inertial to viscous forces. Low values (Re < ~10 – 500) imply that viscous forces predominate, so that flow tends to be laminar and smooth, whereas large values lead to turbulence, with chaotic eddies and instabilities. An expression for the Reynolds number, and some comments about its magnitude, are provided here.
For laminar flow, the basic equation of fluid motion (the Navier-Stokes equation) can be solved to give Stokes law (relating the frictional (drag) force on a body to its size and relative velocity in a fluid), which is provided here.
By setting this force equal to the net gravitational force, the steady state (terminal) velocity of a (spherical) body falling under gravity in a static fluid can be obtained as:
\[u_{ter} = \frac{d^2 \Delta \rho g}{18 \eta} \]
where Δρ is the difference in density, d is the particle size, g is the acceleration due to gravity and ν is the viscosity of the fluid. For a typical (ρ ~ 4000 kg m-3) powder particle, of diameter 100 μm, falling freely in air, this velocity is about 1 m s-1. Of course, for smaller particles it is much lower (uter ~ 0.1 mm s-1 for 1 μm diameter), so that such fine particulate has a very slow sedimentation rate and readily tends to become, and remain, airborne. The simulation below allows exploration of terminal velocity values for various cases, and also shows how this velocity is approached by a particle that is initially at rest in the fluid. Once 'Start' has been clicked, the particle size and density, and the type of fluid, can be changed while the simulation is running, which may be helpful in exploring the sensitivity of the behaviour to these variables.
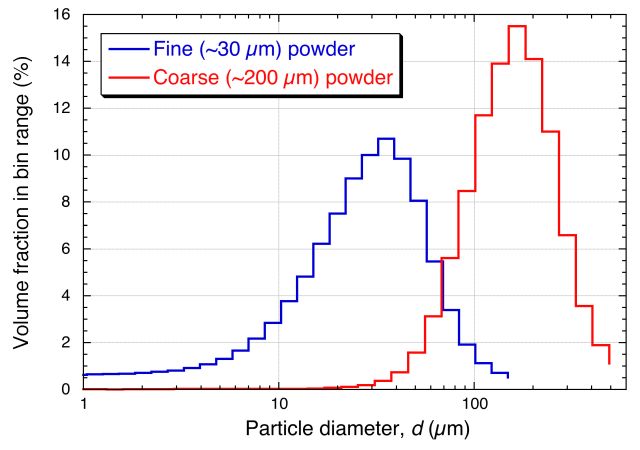
Provided below are four short videos, showing the outcome of inverting small transparent containers in which there are particles suspended in a liquid. For two of them, the liquid is water, while for the other two it is (rapeseed) oil. In each case, there are either small (average diameter ~ 30 µm) or large (average diameter ~ 200 μm) particles present in the liquid. (The size distribution for these two sets of particles is shown at the end of this page: the particles are volcanic ash, with a density of about 2.5 Mg m-3, so that Δρ is in all cases ~ 1.5 Mg m-3)
For coarse particles in water, the terminal velocity is ~ tens of mm/s, so particles pass though the field of view in about a second or so and it takes less than a minute for essentially all of the particles to have fallen to the base of the container.
https://www.doitpoms.ac.uk/tlplib/po..._200micron.mp4
Coarse particles in Water (Viscosity ~ 10-3 Pa s) - uter ~ 30 mm s-1
With finer particles, the terminal velocity is ~ 1 mm/s. Particles now take something like 20 s to pass though the field of view and they are more susceptible in the initial period to being carried upwards by the convection currents. In this case, it takes several minutes for the liquid to become clear.
https://www.doitpoms.ac.uk/tlplib/po...r_30micron.mp4
Fine particles in Water (Viscosity ~ 10-3 Pa s) - uter ~ 1 mm s-1
The rapeseed oil has a much higher viscosity than water, so even the coarse particles sediment slowly, taking several tens of seconds to pass through the field of view and it takes about 20 minutes for the liquid to become clear again.
https://www.doitpoms.ac.uk/tlplib/po..._200micron.mp4
Coarse particles in Oil (Viscosity ~ 5 10-2 Pa s) - uter ~ 0.5 mm s-1
Fine particles in the oil have a very low terminal velocity (of a few tens of microns per second). They can take periods of a minute or more to pass through the field of view, and in fact it can be seen that particles can readily be carried upwards by convection currents. However, another effect is also apparent here - there is a tendency for these fine particles to clump together in this viscous liquid and relatively dense agglomerates of this type behave differently, tending to fall with a higher velocity, in a similar way to that expected with much larger particles.
https://www.doitpoms.ac.uk/tlplib/po...l_30micron.mp4
Fine particles in Oil (Viscosity ~ 5 10-2 Pa s) - uter ~ 0.02 mm s-1
The Particle Size Distributions for the two powder samples in the above videos are shown below. (These were obtained by Laser Scattering - see the next page.)