Skip to main content
Engineering LibreTexts

17.10: Questions

  1. Last updated
  2. Save as PDF
  • Page ID
    36620

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Quick questions

    You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

    The Reynolds number is a measure of:

    a The ratio of inertial forces to viscous forces, and hence of the tendency for fluids to flow faster.
    b The ratio of inertial forces to viscous forces, and hence of the tendency for fluids to flow more slowly.
    c The ratio of inertial forces to viscous forces, and hence of the tendency for fluid flow to become chaotic.
    d The ratio of the speed of a fluid to its dynamic viscosity, and hence of the tendency for fluid flow to become chaotic.
    Answer

    C

    The terminal velocity of a particle falling under gravity in a fluid is:

    a Proportional to the square of its size.
    b Independent of its shape.
    c Independent of the fluid viscosity.
    d Independent of temperature.
    Answer

    A

    The Stokes number is a measure of:

    a The ratio of the velocity of a particle in a fluid to the velocity of an obstacle in its path, and hence of the likelihood of it striking the obstacle.
    b The ratio of the velocity at which a particle in a fluid is approaching an obstacle, to its terminal velocity in the fluid, and hence of the likelihood of it striking the obstacle.
    c The ratio of the inertial force acting on a particle moving towards an obstacle, to the drag force exerted by the fluid, and hence of the likelihood of it striking the obstacle.
    d The time needed for a particle to change its direction of motion, relative to that involved in passing an obstacle in its path, and hence of the likelihood of it striking the obstacle.
    Answer

    D

    The (specific) permeability of a porous medium is:

    a The proportionality constant relating the flux of a fluid through the medium to the pressure gradient divided by the fluid viscosity.
    b Directly proportional to its porosity.
    c The proportionality constant relating the average velocity of a fluid flowing through the medium to the pressure gradient divided by the fluid viscosity.
    d Independent of the specific surface area of the medium.
    Answer

    A

    The sintering process that leads to a relatively loose assembly of powder particles being transformed into a material with acceptable strength and stiffness:

    a Always involves removal of most or all of the porosity.
    b Requires the application of imposed pressure at high temperature.
    c Is driven by reduction of the surface area within the powder assembly.
    d Involves flow of a liquid and/or chemical reactions.
    Answer

    C

    Deeper questions

    The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

    It is proposed that a new type of Diesel Particulate Filter (DPF), with a very high efficiency for extracting fine carbon particles, could be made by creating a bonded assembly of fine alumina fibres (diameter ~0.1 μm). Use the Carman-Kozeny equation to estimate the expected permeability of such a material, assuming that it will be 80% porous. If the maximum gas flux through the DPF is 500 m3 hr-1, its surface area is ~1 m2 and its wall thickness is ~1 mm, estimate the pressure drop across it and comment on whether this value is likely to be acceptable for satisfactory operation of the engine. [The viscosity of the exhaust gas at the temperature concerned is about 3 10-5 Pa s.]

    Answer

    All that is required to use the C-K equation is the value of S. For an open assembly of (long) fibres, taking the total volume as V, the porosity as P, the total fibre length as L and the fibre radius as R:

    \[V_{fib} = \left( {1 - P} \right)V = L\left( {\pi {R^2}} \right)\]
    so the value of S can be expressed as

    \[S = \frac{L\left( {2\pi R} \right)}{V} = \frac{\left( {1 - P} \right)L\left( {2\pi R} \right)}{L\left( {\pi {R^2}} \right)} = \frac

    ParseError: EOF expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[1]/dd/p[3]/span, line 1, column 2
    {R} = \frac{0.4}{{{10^{ - 7}} = 4\;{10^6}\;{\rm{m}^2}\;{\rm{m}^{-3}}\]

    The permeability is thus given by

    \[\kappa = \frac

    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[1]/dd/p[5]/span[1], line 1, column 3
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[1]/dd/p[5]/span[2], line 1, column 3
    = \frac
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[1]/dd/p[5]/span[3], line 1, column 2
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[1]/dd/p[5]/span[4], line 1, column 3
    \approx 2\;{10^{ - 13}}\;{{\rm{m}}^2}\]

    Darcy's law can now be used to estimate the required pressure drop

    \[\Delta p = \frac{Q\eta \Delta x}{\kappa } = \frac{500\left( 3\; 10^{-5} \right)10^{-3}} {3600\left( 2 \;{10^{-13} \right)} \approx 2\;10^4 \; \rm{Pa} \approx 0.2\;\rm{bar}\]

    It is proposed that thermal spraying will be used to create an alumina (MPt. ~2040˚C) coating on a metal artefact, using a combustion torch with a flame temperature of 2300˚C. The alumina powder to be used has an average particle size of about 20 µm and the heat capacity of alumina c, is ~3 106 J m-3 K-1. The stand-off distance to be used is 400 mm and the gas velocity is 200 m s-1. The interfacial heat transfer coefficient under these conditions is estimated to be 10 kW m-2 s-1. Assuming that injected particles reach the gas velocity very quickly, estimate their temperature at impact and hence decide whether the spraying process is likely to be successful.

    Answer

    The key issue here is the particle temperature at impact, Ti, after a flight time of tf in contact with gas at a temperature Tg (flame temperature). It can be assumed that, during thermal spraying, particles will remain approximately isothermal throughout (Bi<<1). The heating rate can be obtained from the heat flux across the interface, which is dictated by the temperature difference ΔT and the heat transfer coefficient, hi:

    \[\begin{array}{l}{h_{\rm{i}}}\Delta T\left( {4\pi

    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[1], line 1, column 1
    \right) = c\left( {\frac
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[2], line 1, column 2
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[3], line 1, column 2
    } \right)\left( {\frac{4}{3}\pi
    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[4], line 1, column 1
    \right)\\∴ \frac
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[5], line 1, column 2
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[6], line 1, column 2
    = \frac
    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[7], line 1, column 5
    UndefinedNameError: reference to undefined name 'cd' (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[2]/span[8], line 1, column 1
    \end{array}\]

    The heating rate thus drops during flight, as the temperature difference across the interface becomes smaller. The above equation can be used to relate the flight time to the corresponding temperature change of the particle (from T0 to Ti), in integral form:

    \[{t_{\rm{f}}} = \int\limits_0^

    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[1], line 1, column 4
    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[2], line 1, column 1
    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[3], line 1, column 5
    \int\limits_
    UndefinedNameError: reference to undefined name 'T_0' (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[4], line 1, column 1
    ^
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[5], line 1, column 4
    {\frac
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[6], line 1, column 2
    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[4]/span[7], line 1, column 1
    } \]

    Carrying out the integration:
    \[\begin{array}{l}{t_{\rm{f}}} = \frac

    UndefinedNameError: reference to undefined name 'cd' (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[1], line 1, column 1
    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[2], line 1, column 5
    \left[ {\ln \left( {\frac
    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[3], line 1, column 4
    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[4], line 1, column 4
    } \right)} \right]\\∴ {T_{\rm{i}}} = {T_{\rm{g}}} - \left(
    ParseError: "}" expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[5], line 1, column 4
    \right)\exp \left( {\frac
    ParseError: colon expected (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[6], line 1, column 8
    UndefinedNameError: reference to undefined name 'cd' (click for details)
    Callstack:
    at (Bookshelves/Materials_Science/TLP_Library_II/17:_Powder_Processing/17.a10:_Questions), /content/body/div[2]/dl[2]/dd/p[5]/span[7], line 1, column 1
    } \right)\end{array}\]

    Since it is being assumed that the particle instantly reaches the gas velocity, u (= 200 m s-1), and the flight distance is 400 mm, the flight time is 2 ms. The particle temperature at impact is therefore given by:

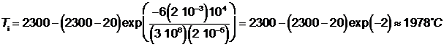
    This is below the melting point and so there would be a concern about the particles being sufficiently soft. (In fact, in order to melt the particles, it would also be necessary to inject the required latent heat, so they would be some way from being molten.) The spraying is therefore not expected to be successful.

    This page titled 17.10: Questions is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Dissemination of IT for the Promotion of Materials Science (DoITPoMS) via source content that was edited to the style and standards of the LibreTexts platform.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      DoITPoMS
      License
      CC BY-NC-SA
      Show TOC
      no
    2. Tags
      1. source@https://www.doitpoms.ac.uk