21.6: The Ellingham Diagram in Removal of Contaminants
- Page ID
- 43535
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The recycling of metals is a metallurgical process, and as such can be described by the rules of thermodynamics. Earlier on this was illustrated by the energy considerations of Aluminium production. On the most basic level, if the free energy of the reactants in a chemical reaction is different to that of the products, a reaction will occur. The reaction will stop when the free energies of the products and the reactants are equal. Contaminants in recycling molten metal ‘solutions’ are removed using the principles of oxidation and reduction, which can be described graphically on the Ellingham Diagram.
The Ellingham diagram shows the changes in standard free energy that occur in various reactions. In this TLP the focus is on oxidation reactions. The free energy change for oxidation reactions can be given by:
ΔG = ΔG0 − RT lnE
where K is the equilibrium constant, calculated from:
activity (metal oxide) / activity (pO2)x
where x is the number of moles of O2 in the reaction (i.e. if the reaction is Metal + 1/2O2 → MetalO, then this index = 1/2)
At equilibrium, ΔG = 0, so if ΔG = ΔG + RT lnG ΔG0 = − RT lnK.
Plotting T against ΔG0 gives the Ellingham diagram.
The oxidation Ellingham diagram is used to find the partial pressures of oxygen needed to oxidise elements at a given temperature, or reduce the metal oxide. The vertical difference between ΔG values of two lines at a specific temperature gives ΔG values used in redox reactions like the energy for primary aluminium production, explored further up in this TLP.
In the EAF, under oxidising conditions (bubbling oxygen gas through the molten metal) elements such as aluminium, silicon, manganese and chromium can be oxidised to the slag. The Ellingham diagram is used to determine the oxygen partial pressure being bubbled through the molten metal:
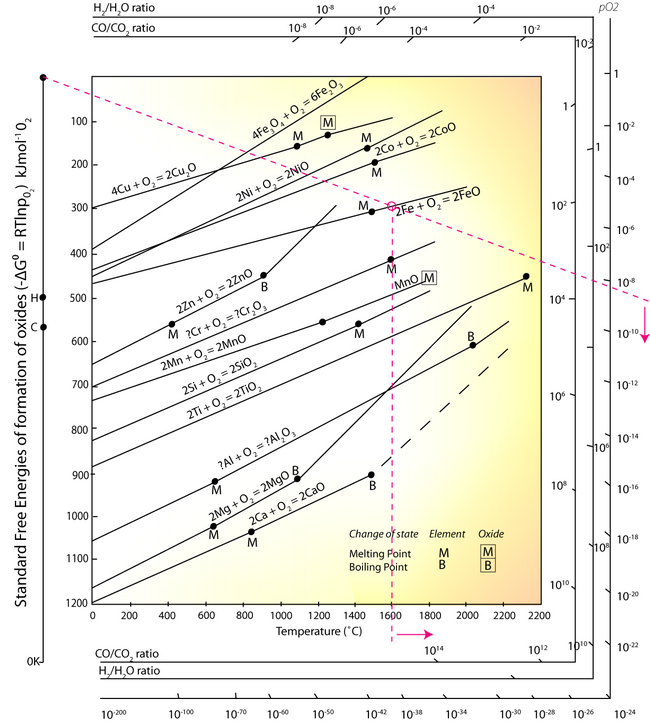
- Identify a point corresponding to a selected temperature on the line for: Fe + O → FeO, above M.
- Using this point, and the point O in the top left corner, draw a line across the diagram.
- Read the partial pressure of O2 from the right hand axis.
At any oxygen pressure higher than ~10-8.5, the iron will be oxidised at the temperature of 1600°C. It can be seen from the Ellingham diagram that the equilibrium lines of Aluminium, Silicon, Manganese and Chromium equilibrium lines are at a lower free energy position than the 2Fe + O2 → 2FeO line, and so at any partial pressure of oxygen all of these elements will be oxidised into the slag. However, Sulphur and Phosphorus cannot be removed from the steel melt by simple oxidation, other methods have to be employed.
Phosphorus oxidation is possible under very basic conditions by reducing the activity of the oxidised P2O5 in the slag, therefore altering very significantly the value of.
Sulphur can be removed also in a basic slag but under a reducing condition, by the addition of lime (desulphurization ):
FeS + CaO → CaS + FeO
For making alloy steels, it is also possible to preserve alloying elements such as Ni or Mo by using a reducing slag in the EAF.
Copper and Tin are examples of elements that cannot be refined out of steel in the EAF (or the BOF) illustrating the importance of the de-tinning process and the removal of copper from motors explored earlier in the TLP. These elements render steel very difficult to process due to hot shortness during hot rolling. It is important to control these elements at very low levels in steel. As they cannot be refined in the BOF or EAF, they will accumulate in steel and increase in successive generations. If we do not find a suitable large-scale method for removing these elements, the success of steel recycling in the future will be seriously limited. This issue is explored quantitatively in the Deeper Questions section of the TLP.


