3.3: Specification to the 2-D Continuum
- Page ID
- 21485
Plane Stress
This is the state of stress that develops in thin plates and shells so it requires a careful consideration. The stress state in which \(\sigma_{3j} = 0\), where the \(x_3 = z\) axis is in the through thickness direction. The non-zero components of the stress tensor are:
\[\sigma_{ij} = \begin{vmatrix}
\sigma_{11} & \sigma_{12} & 0 \\
\sigma_{21} & \sigma_{22} & 0 \\ 0 & 0 & 0
\end{vmatrix} \; \epsilon_{ij} = \begin{vmatrix}
\epsilon_{11} & \epsilon_{12} & 0 \\
\epsilon_{21} & \epsilon_{22} & 0 \\ 0 & 0 & \epsilon_{33}
\end{vmatrix}\]
where \(i, j = 1, 2, 3\) and \(\alpha, \beta = 1, 2\). Accordingly, \(\sigma_{kk} = \sigma_{11} + \sigma_{22} + \sigma_{33} = \sigma_{\gamma\gamma} + 0\). The 2-D elasticity law takes the following form in the tensor notation
\[\epsilon_{\alpha \beta} = \frac{1 + \nu}{E} \sigma_{\alpha \beta} − \frac{\nu}{E} \sigma_{\gamma\gamma} \delta_{\alpha \beta} \label{3.3.2}\]
It can be easily checked from Equation \ref{3.3.2} that in plane stress \(\epsilon_{13} = \epsilon_{23} = 0\) but \(\epsilon_{33} = − \frac{\nu}{E} (\sigma_{11}+\sigma_{22})\). The through-thickness component of the strain tensor is not zero. Because it does not enter the plane stress strain-displacement relation, its presence does not contribute to the solutions. It can only be determined afterwards from the known stresses \(\sigma_{11}\) and \(\sigma_{22}\).
By making contraction \(\epsilon_{kk} = \frac{1 − \nu} {E} \sigma_{kk}\), one can easily invert Equation \ref{3.3.2} in the form
\[\sigma_{\alpha \beta} = \frac{E}{1 + {\nu}^2} [(1-\nu)\epsilon_{\alpha \beta} + \nu \epsilon_{\gamma\gamma} \delta_{\alpha \beta}] \]
The above equation is a starting point for deriving the elasticity law in generalized quantities for plates and shells. We shall return to that task later in this lecture. Before that, let’s discuss three other important limiting cases
\[\sigma_{11} = \frac{E}{1 - {\nu}^2}(\epsilon_{11} + \nu\epsilon_{22})\]
\[\sigma_{22} = \frac{E}{1 - {\nu}^2} (\epsilon_{22} + \nu\epsilon_{11})\]
\[\sigma_{13} = \frac{E}{1 + {\nu}} \epsilon_{12} \]
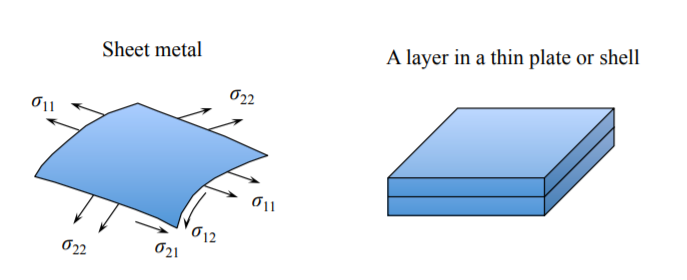
Plane strain holds whenever \(\epsilon_{2j} = 0\). By imposing a constraint on \(\epsilon_{22} = 0\), a reaction immediately develops in the direction as \(\sigma_{22} \neq = 0\).
The components of the strain and Equations (3.2.12-3.2.13) stress tensors are
\[\epsilon_{ij} = \begin{vmatrix}
\epsilon_{11} & \epsilon_{12} & 0 \\
\epsilon_{21} & \epsilon_{22} & 0 \\ 0 & 0 & 0
\end{vmatrix} \; \sigma_{ij} = \begin{vmatrix}
\sigma_{11} & \sigma_{12} & 0 \\
\sigma_{21} & \sigma_{22} & 0 \\ 0 & 0 & \sigma_{33}
\end{vmatrix}\]
Can you show that under the assumption of the plane strain, the reaction stress \(\sigma_{33} = \nu(\sigma_{11} + \sigma_{22})\)? The plane strain is encountered in many practical situations, such as cylindrical bending of a plate or wide beam.
Uniaxial Strain
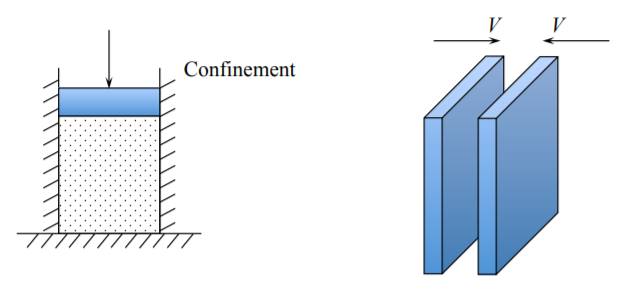
Uniaxial strain is achieved when the displacement in two directions are constrained. For example, soil or granular materials are tested in a cylinder (called confinement) with a piston, Figure (\(\PageIndex{3}\)). The uniaxial strain also develops in a compressed layer between two rigid plates. Also high velocity plate-to-plate impact products the one-dimensional strain. Here the only component of the strain tensor is the volumetric strain. The plate-to-plate experiments are conducted to establish the nonlinear compressibility of metals under very high hydrostatic loading \(\sigma_{kk} = −3p\). Similarly, the plane wave in the 3-D space is generating a uniaxial strain.
The components of the stress and strain tensor in the uniaxial strain are:
\[\sigma_{ij} = \begin{vmatrix}
\sigma_{11} & \sigma_{12} & 0 \\
\sigma_{21} & \sigma_{22} & 0 \\ 0 & 0 & \sigma_{33}
\end{vmatrix} \; \epsilon_{ij} = \begin{vmatrix}
\epsilon_{11} & 0 & 0 \\
0 & 0 & 0 \\ 0 & 0 & 0
\end{vmatrix}\]
Where the reaction stresses are related to the active stress \(\sigma_{11}\) by \(\sigma_{22} = \sigma_{33} = \frac{\nu(1 + \nu)\sigma_{11}}{1 − \nu^2}\). Can you prove that?
The uniaxial stress state was discussed earlier in this lecture when converting the Lame’ constants into the engineering constants \((E, \nu)\).


