8.3: Stability of Elastic Column Using the Energy Method
- Page ID
- 21520
The Trefftz condition for stability can now be extended to the elastic column subjected to combined bending and compression. The elastic strain energy stored in the column is a sum of the bending and axial force contribution
\[U = \int_{0}^{l} \left( \frac{1}{2} M \kappa + \frac{1}{2} N \epsilon_o \right) dx \]
It is assumed that the column is fixed at one end against axial motion and allow to move in the direction of the axial force.
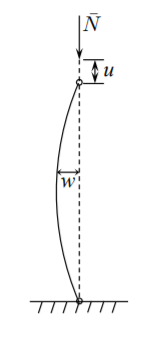
To maintain generality, no static or kinematic boundary conditions are introduced in the present derivation. The work of external forces is
\[W = \bar{N}u_o \]
The first variation of the total potential energy is
\[\delta\prod = \delta (U − W) = \frac{1}{2} \int_{0}^{l} (\delta M\kappa + M\delta\kappa + \delta N \epsilon + N\delta \epsilon)dx − N\delta u_o \label{8.3.3}\]
For linear elastic material
\[M = EI \kappa, \quad \delta M = EI \delta \kappa \]
\[N = EA \epsilon, \quad \delta N = EA \delta \epsilon \]
By eliminating the bending and axial rigidity between the above equation, the following identities hold
\[M \delta \kappa = \delta M \kappa \]
\[N \delta \epsilon = \delta N \epsilon\]
Therefore, the expression \ref{8.3.3} is reduced to
\[\delta\prod = \int_{0}^{l} (M\delta \kappa + N\delta \epsilon) dx − \bar{N}\delta u_o \label{8.3.8}\]
Now, recall the strain-displacement relations in the theory of moderately large deflection of beams
\[\kappa = −w^{\prime \prime}, \quad \delta \kappa = −(\delta w)^{\prime \prime} \]
\[\epsilon = u^{\prime} + \frac{1}{2} (w^{\prime})^2 , \quad \delta\epsilon = (\delta u)^{\prime} − w^{\prime} \delta w^{\prime} \]
Substituting the increments \(\delta\kappa\) and \(\delta\epsilon\) into Equation \ref{8.3.8} yields
\[\delta \prod = − \int_{0}^{l} M \delta w^{\prime \prime} dx + N \int_{0}^{l} w^{\prime} \delta w^{\prime} dx + N \int_{0}^{l} \delta u^{\prime} dx − N\delta u_o \label{8.3.11}\]
In the above expression the axial load is unknown but constant over the length of the column. Therefore the load \(N\) could be brought outside the integrals. Consider now the last two terms in Equation \ref{8.3.11}
\[N \int_{0}^{l} \delta u^{\prime} dx − N\delta u_o = \left. N\delta u\right|^{x=l}_{x=0} − N\delta u = N\delta u_o − N\delta u_o = 0 \]
With the above simplification we calculate now the second variation of the total potential energy
\[\delta^2 \prod = \delta (\delta\prod) = − \int_{0}^{l} \delta M\delta w^{\prime \prime} dx + N \int_{0}^{l} \delta w^{\prime} \delta w^{\prime} dx \]
According to the Trefftz stability criterion \(\delta^2\prod = 0\),
\[− \int_{0}^{l} EI \delta w^{\prime\prime} \delta w^{\prime\prime} dx + N \int_{0}^{l} \delta w^{\prime} \delta w^{\prime} dx = 0 \]
The buckling load \(N = N_c\) is then
\[N = EI \frac{− \int_{0}^{l}\delta w^{\prime\prime} \delta w^{\prime\prime} dx}{\int_{0}^{l} \delta w^{\prime} \delta w^{\prime} dx} \label{8.3.15}\]
Let’s express the out-of-plane deflection of the column as a product of the amplitude \(A\) and the normalized shape function \(\phi(x)\). The shape function should satisfy kinematic boundary condition of a problem
\[w(x) = A \phi (x) \]
We can calculate now the first and second derivatives of the function \(w(x)\) and their variations
\[w^{\prime} = A\phi^{\prime}, \quad \delta w^{\prime} = \delta A\phi^{\prime} \]
\[w^{\prime\prime} = A\phi^{\prime\prime}, \quad \delta w^{\prime\prime} = \delta A\phi^{\prime\prime}\]
Substituting the above expression into Equation \ref{8.3.15}, we get
\[N_c = EI \frac{\int_{0}^{l} \delta A\phi^{\prime\prime} \delta A\phi^{\prime\prime} dx }{\int_{0}^{l} \delta A\phi^{\prime} \delta A\phi^{\prime} dx} = EI \frac{\int_{0}^{l} \phi^{\prime\prime} \phi^{\prime\prime} dx}{\int_{0}^{l} \phi^{\prime} \phi^{\prime} dx} \]
where \(N_c = -N\) is he compressive buckling load.
The above equation for the critical buckling load of a column is called the Raleigh-Ritz quotient. The Trefftz criterion does not provide the shape function but for a given shape calculates the approximate value of the buckling load. This is always an upper bound. Should the shape function coincide with the exact buckling shape, the Raleigh-Ritz quotient will give the absolute minimum value.
As an illustration, consider the pin-pin supported column and assume the following buckling shape
\[\phi (x) = x(l − x) \label{8.3.20}\]
which satisfies identically kinematic boundary conditions \(\phi (x = 0) = \phi (x = l) = 0\). The first and second derivatives of the shape function are
\[\phi^{\prime} (x) = 2x − l \]
\[\phi^{\prime\prime} (x) = 2 \]
After straightforward integration, the calculated buckling load is
\[N_c = \frac{12EI}{l^2} \]
Can the accuracy of the above solution be improved? Let’s try and assume as a shape function the solution for the pin-pin beam under the uniform line load
\[\phi (x) = x^4 − 2lx^3 + l^3x \]
The above function satisfies the simple support boundary condition at both ends. The slope and the curvature of the deflected shape are
\[\phi^{\prime}(x) = 4x^3 − 6lx^2 + l^3 \]
\[\phi^{\prime\prime}(x) = 12x^2 − 12lx \]
Because the curvature at both ends vanish, so does the bending moment. Also the slope at mid-span is zero. This means that the static (zero bending moments) boundary conditions are also satisfied. The previously considered shape function, Equation \ref{8.3.20} led to the constraint curvature, meaning that the static boundary conditions were violated. After straightforward calculation, the numerical coefficient become \(\frac{1680}{170} = 9.88\). There was over 20% improvements in the accuracy of the solution
\[N_c = 9.88 \frac{EI}{l^2} \]
Can the solution be further improved (lowered)? yes, but not by much. Assume a sinusoidal shape of the buckling shape
\[\phi = \sin \frac{\pi x}{l} \label{8.3.28}\]
\[\phi^{\prime} = \frac{\pi}{l} \cos \frac{\pi x}{l} \]
\[\phi^{\prime\prime} = − \left(\frac{\pi}{l}\right)^2 \sin \frac{\pi x}{l} \label{8.3.30}\]
The expression for the critical buckling load becomes
\[N_c = \frac{EI(\frac{\pi}{l})^4}{(\frac{\pi}{l})^2} \frac{\int_{0}^{l} \sin^2 \frac{\pi x}{l} dx} {\int_{0}^{l} \cos^2 \frac{\pi x}{l} dx} \]
Both integrals are identical and the solution becomes
\[N_c = \frac{ \pi^2 EI}{l^2} \label{8.3.32}\]
Because \(\pi^2 = 9.86\), the sinusoidal solution is slightly lower than the previous polynomial solution. This is the lowest possible coefficient meaning that it must be an exact solution to the buckling problem. To prove it, it is sufficient to check if the local equilibrium equation is satisfied
\[EIw^{\mathrm{IV}} + Nw^{\prime\prime} = 0 \]
Indeed, substituting Equations \ref{8.3.28} - \ref{8.3.30} and \ref{8.3.32} into the equilibrium equation brings the left hand side of this equation identically to zero.


