3.3: Determinacy and Stability of Beams and Frames

Prior to the choice of an analytical method, it is important to establish the determinacy and stability of a structure. A determinate structure is one whose unknown external reaction or internal members can be determined using only the conditions of equilibrium. An indeterminate structure is one whose unknown forces cannot be determined by the conditions of static equilibrium alone and will require, in addition, a consideration of the compatibility conditions of different parts of the structure for its complete analysis. Furthermore, structures must be stable to be able to serve their desirable functions. A structure is considered stable if it maintains its geometrical shape when subjected to external forces.

Formulations for Stability and Determinacy of Beams and Frames

The conditions of determinacy, indeterminacy, and instability of beams and frames can be stated as follows: \[\begin{array}{l} 3 m+r<3 j+C \text { Structure is statically unstable} \\ 3 m+r=3 j+C \text { Structure is statically determinate}\\ 3 m+r>3 j+C \text { Structure is statically indeterminate} \end{array}\]

where

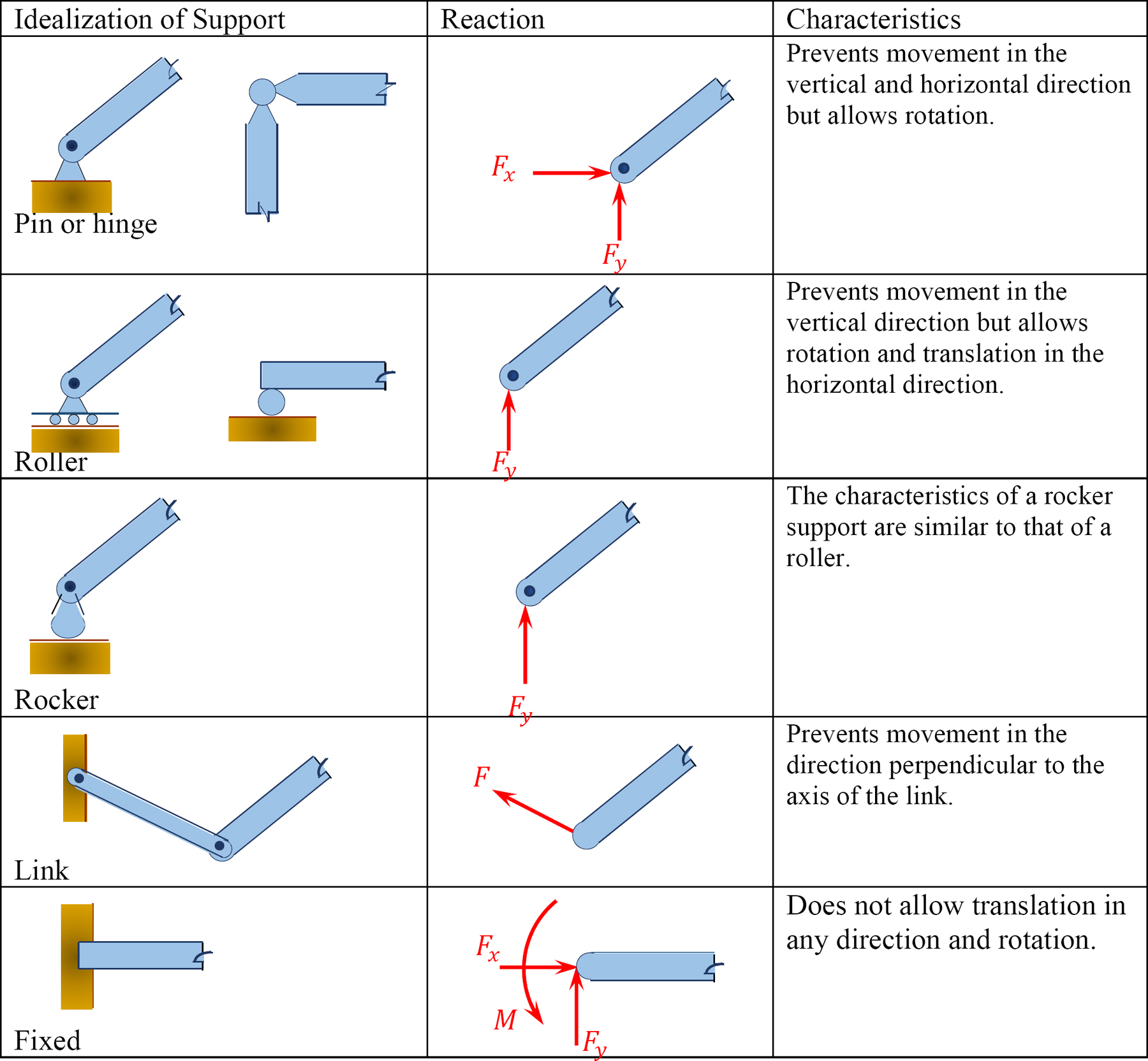
• \(r\) = number of support reactions.
• \(C\) = equations of condition (two equations for one internal roller and one equation for each internal pin).
• \(m\) = number of members.
• \(j\) = number of joints.

\(Table 3.1\). Types of supports.

Alternative Formulation for Determinacy and Stability of Beams and Frames

\[\begin{array}{l} r+F_{i}<3 m \text { Structure is statically unstable}\\ r+F_{i}=3 m \text { Structure is statically determinate}\\ r+F_{i}>3 m \text { Structure is statically indeterminate} \end{array}\]

where

• \(r\) = number of support reactions.
• \(F_{i}\) = number of reaction forces transmitted by an internal hinge or internal roller.
• \(m\) = number of members.

Example 3.1

Classify the beams shown in Figure 3.1 through Figure 3.5 as stable, determinate, or indeterminate, and state the degree of indeterminacy where necessary.

\(Fig. 3.1\). Beam.

Solution

First, draw the free-body diagram of each beam. To determine the classification, apply equation 3.3 or equation 3.4.

Using equation 3.3, \(r = 7\), \(m = 2\), \(c = 0\), \(j = 3\). Applying the equation leads to \(3(2)+7>3(3)+0\), or \(13 > 9\). Therefore, the beam is statically indeterminate to the \(4^{\circ}\).

Using equation 3.4, \(r = 7\), \(m = 1\), \(F_{i} = 0\). Applying the equation leads to \(7+0>(3)(1)\), or \(7 > 3\). Therefore, the beam is statically indeterminate to the \(4^{\circ}\).

Note: When using equation 3.3, the portions on either side of the interior support are counted as separate members.

\(Fig. 3.2\). Beam.

Solution

Using equation 3.3, \(r = 6\), \(m = 3\), \(c = 0\), \(j = 4\). Applying the equation leads to \(3(3) + 6 > 3(4) + 0\), or \(15 > 12\). Therefore, the beam is statically indeterminate to the \(3^{\circ}\).

Using equation 3.4, \(r = 6, \(m = 1\), \(F_{i} = 0\). Applying the equation leads to \(6 + 0 > (3)(1)\), or \(6 > 3\). Therefore, the beam is statically indeterminate to the \(3^{\circ}\).

\(Fig. 3.3\). Beam.

Solution

Using equation 3.3,\(r = 5\), \(m = 3\), \(c = 1\), \(j = 4\). Applying the equation leads to \(3(3) + 5 > 3(4) + 1\), or \(14 > 13\). Therefore, the beam is statically indeterminate to the \(1^{\circ}\).

Using equation 3.4, \(r = 5\), \(m = 2\), \(F_{i} = 2\). Applying the equation leads to \(5 + 2 > 3(2)\), or \(7 > 6\). Therefore, the beam is statically indeterminate to the \(1^{\circ}\).

\(Fig. 3.4\). Beam.

Solution

Using equation 3.3, \(r = 5\), \(m = 4\), \(c = 1\), \(j = 5\). Applying the equation leads to \(3(4) + 5 > 3(5) + 1\), or \(17 > 16\). Therefore, the equation is statically indeterminate to the \(1^{\circ}\).

Using equation 3.4, \(r = 5\), \(m = 2\), \(F_{i} = 2\). Applying the equation leads to \(5 + 2 > 3(2)\), or \(7 > 6\). Therefore, the beam is statically indeterminate to the \(1^{\circ}\).

\(Fig. 3.5\). Beam.

Solution

Using equation 3.3, \(r = 5\), \(m = 5\), \(c = 2\), \(j = 6\). Applying the equation leads to \(3(5) + 5 = 3(6) + 2\), or \(20 = 20\). Therefore, the beam is statically determinate.

Using equation 3.4, \(r = 5\), \(m = 3\), \(F_{i} = 4\). Applying the equation leads to \(5 + 4 > 3(3)\), or \(9 = 9\). Therefore, the beam is statically determinate.

Example 3.2

Classify the frames shown in Figure 3.6 through Figure 3.8 as stable or unstable and determinate or indeterminate. If indeterminate, state the degree of indeterminacy.

\(Fig. 3.6\). Frame.

Solution

Using equation 3.3, \(r = 3\), \(m = 3\), \(c = 0\), \(j = 4\). Applying the equation leads to \(3(3) + 3 = 3(4) + 0\), or \(12 = 12\). Therefore, the frame is statically determinate.

Using equation 3.4, \(r = 3\), \(m = 1\), \(F_{i} = 0\). Applying the equation leads to \(3 + 0 = (3)(1)\), or \(3 = 3\). Therefore, the frame is statically determinate.

Note: When using equation 3.3 for classifying a frame, the frame must be disassembled at its joints to correctly determine the number of members.

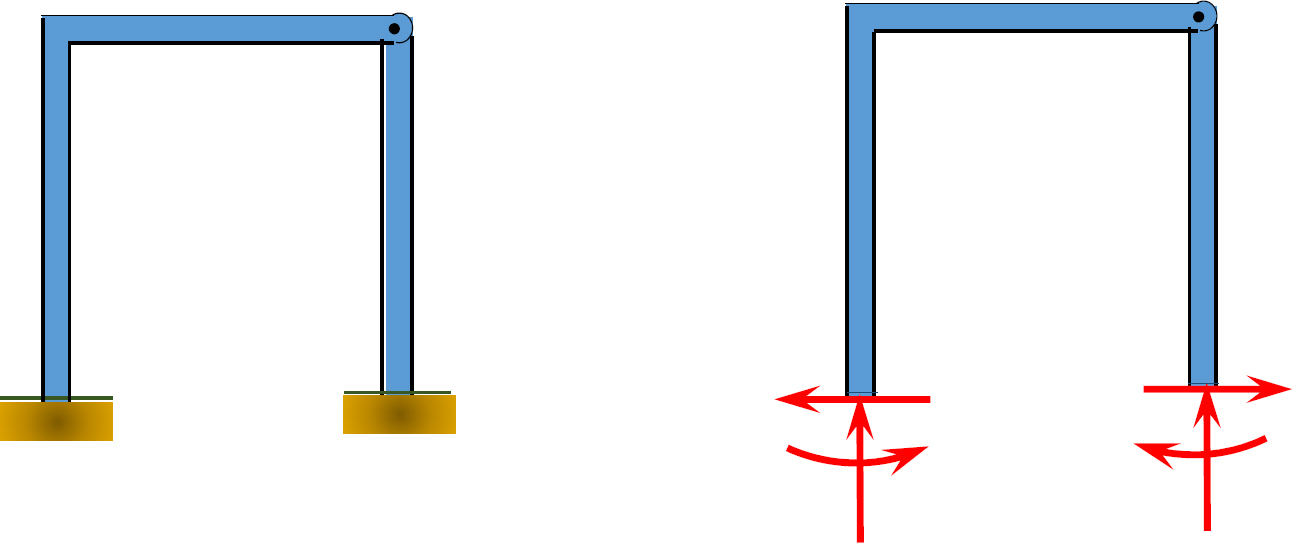
\(Fig. 3.7\). Frame.

Solution

Using equation 3.3, \(r = 6\), \(m = 3\), \(c = 1\), \(j = 4\). Applying the equation leads to \(3(3) + 6 > 3(4) + 1\), or \(15 > 13\). Therefore, the frame is statically indeterminate to the \(2^{\circ}\).

Using equation 3.4, \(r = 6\), \(m = 2\), \(F_{i} = 2\). Applying the equation leads to \(6 + 2 > 3(2)\), or \(8 > 6\). Therefore, the frame is statically indeterminate to the \(2^{\circ}\).

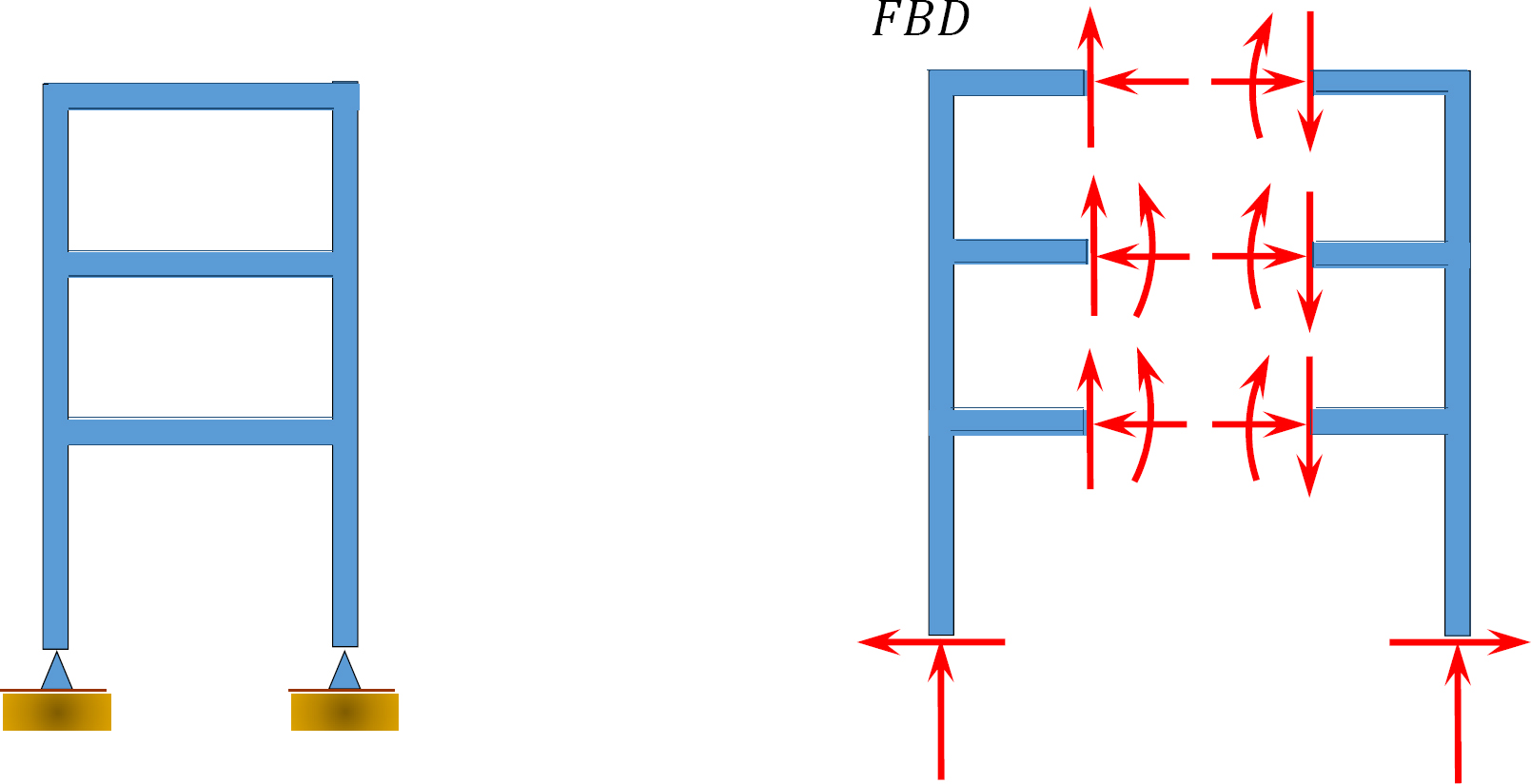
\(Fig. 3.8\). Frame.

Solution

Using equation 3.3, \(r = 4\), \(m = 9\), \(c = 0\), \(j = 8\). Applying the equation leads to \(3(9) + 4 > 3(8) + 0\), or \(31 > 24\). Therefore, the frame is statically indeterminate to the \(7^{\circ}\).

Using equation 3.4, \(r = 4\), \(m = 1\), \(F_{i} = 9\). Applying the equation leads to \(4 + 9 > (3)(2)\), or \(13 > 6\). Therefore, the frame is statically indeterminate to the \(7^{\circ}\).

Note: When using equation 3.4 to classify a frame with a closed loop, as given here, the loop has to be cut open by the method of section, and the internal reactions in the cut section should be considered in the analysis.