10.1: Introduction

Last updated
Save as PDF

Page ID: 42985

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The force method of analysis, also known as the method of consistent deformation, uses equilibrium equations and compatibility conditions to determine the unknowns in statically indeterminate structures. In this method, the unknowns are the redundant forces. A redundant force can be an external support reaction force or an internal member force, which if removed from the structure, will not cause any instability. This method entails formulating a set of compatibility equations, depending on the number of the redundant forces in the structure, and solving these equations simultaneously to determine the magnitude of the redundant forces. Once the redundant forces are known, the structure becomes determinate and can be analyzed completely using the conditions of equilibrium.

For an illustration of the method of consistent deformation, consider the propped cantilever beam shown in Figure 10.1a. The beam has four unknown reactions, thus is indeterminate to the first degree. This means that there is one reaction force that can be removed without jeopardizing the stability of the structure. The structure that remains after the removal of the redundant reaction is called the primary structure. A primary structure must always meet the equilibrium requirement. A careful observation of the structure being considered will show that there are two possible redundant reactions and two possible primary structures (see Fig. 10b and Fig. 10d). Taking the vertical reaction at support \(B\) and the reactive moments at support \(A\) as the redundant reactions, the primary structures that remain are in a state of equilibrium. After choosing the redundant forces and establishing the primary structures, the next step is to formulate the compatibility equations for each case by superposition of some sets of partial solutions that satisfy equilibrium requirements. Equations 10.1 and 10.2 satisfy options 1 and 2, respectively. The terms \(\Delta_{B P}\), \(\theta_{A P}\), \(\delta_{B B}\), and \(a_{A A}\) are referred to as flexibility or compatibility coefficients or constants. The first subscript in a coefficient indicates the position of the displacement, and the second indicates the cause and the direction of the displacement. For example, \(\Delta_{B P}\) implies displacement at point \(B\) caused by the load \(P\) in the direction of the load \(P\). The compatibility coefficients can be computed using the Maxwell-Betti Law of Reciprocal, which will be discussed in the subsequent section.

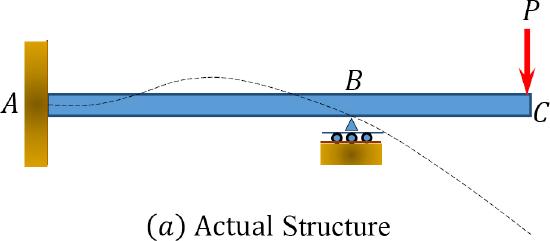
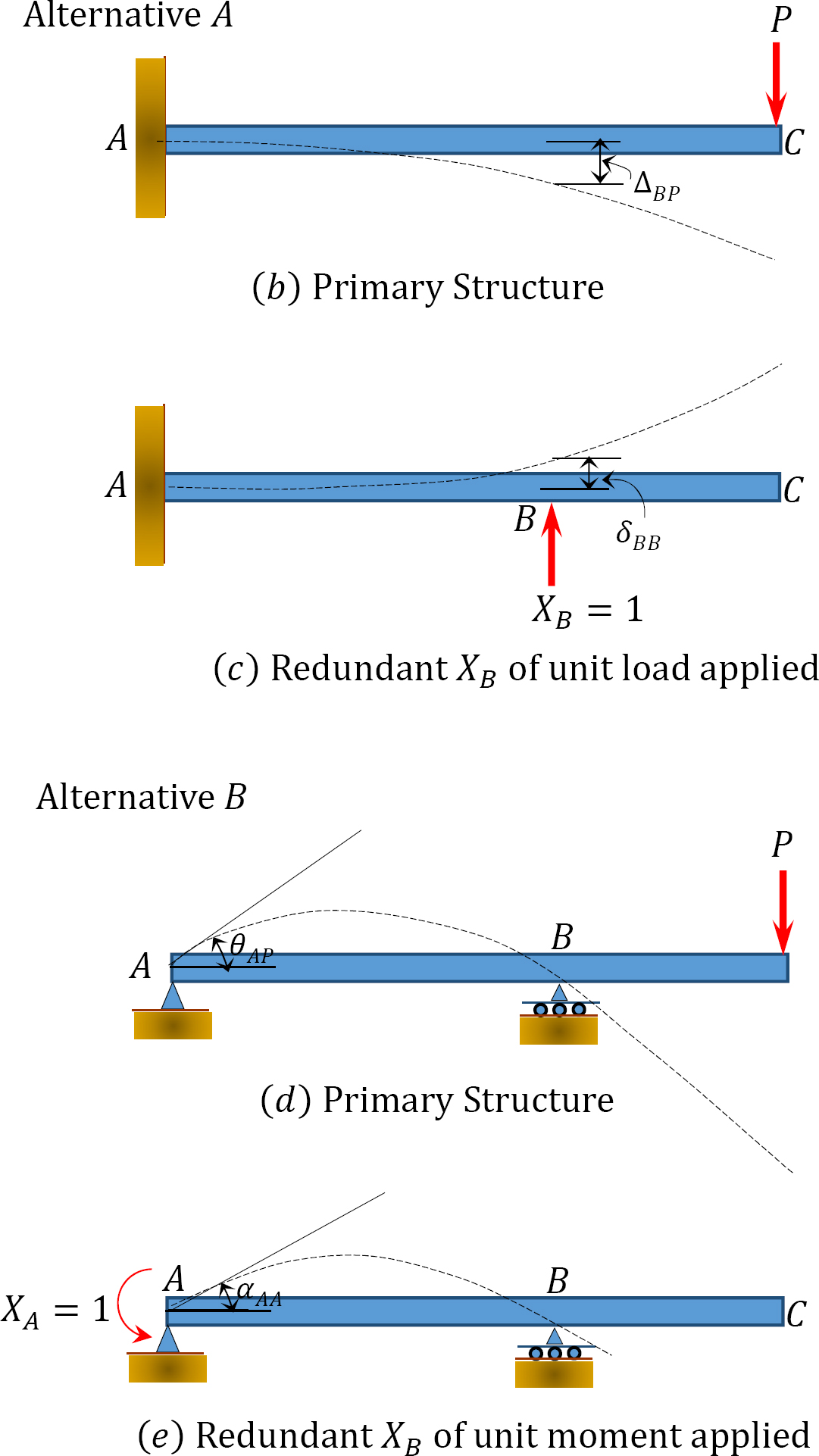
\(Fig. 10.1\). Propped cantilever beam.

\[\Delta_{B P}+R_{B} \delta_{B B}=0\]

\[\theta_{A P}+M_{A} \alpha_{A A}=0\]

where

\(M\) = moment in the primary structure due to the applied load \(P\).

\(m\) = moment in the primary structure due to a unit load applied at \(B\).

\(m_{\theta}\) = moment in the primary structure due to a unit moment applied at \(A\).

Procedure for Analysis of Indeterminate Structures by the Method of Consistent Deformation

•Determine the degree of indeterminacy of the structure.

•Choose the redundant reactions from the indeterminate structure.

•Remove the chosen redundant reactions to obtain the primary structure.

•Formulate the compatibility equations. The number of the equations must match the number of redundant forces.

•Compute the flexibility coefficients.

•Substitute the flexibility coefficients into the compatibility equations.

•In the case of several redundant reactions, solve the compatibility equations simultaneously to determine the redundant forces or moments.

•Apply the computed redundant forces or moments to the primary structure and evaluate other functions, such as bending moment, shearing force, and deflection, if desired, using equilibrium conditions.