6.10: The second law of thermodynamics for open systems

Last updated
Save as PDF

Page ID: 88860

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Entropy can be transferred to a system via two mechanisms: (1) heat transfer and (2) mass transfer. For open systems, the second law of thermodynamics is often written in the rate form; therefore, we are interested in the time rate of entropy transfer due to heat transfer and mass transfer.

\[\dot{S}_{heat} =\dfrac{dS_{heat}}{dt} \cong \displaystyle\sum\dfrac{\dot{Q}_k}{T_k}\]

\[\dot{S}_{mass} = \displaystyle\sum\dfrac{dS_{mass}}{dt} = \displaystyle \sum \dot{m}_{k}s_{k}\]

where

\[\dot{m}\]

\[\dot{Q}_k\]

\[\dot{S}_{heat}\]

\[\dot{S}_{mass}\]

\[s_k\]

Applying the entropy balance equation, 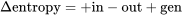$\Delta \rm {entropy= + in - out + gen}$ , to a control volume, see Figure 6.9.1, we can write the following equations:

General equation for both steady and transient flow devices

\[\dfrac

ParseError: colon expected (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[1], line 1, column 4

UndefinedNameError: reference to undefined name 'dt' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[2], line 1, column 1

=\displaystyle\left(\sum

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[3], line 1, column 1

+\displaystyle\sum\frac

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[4], line 1, column 1

UndefinedNameError: reference to undefined name 'T' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[5], line 1, column 1

\right)-\displaystyle\left(\sum

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[6], line 1, column 1

\right)+\displaystyle{\dot

UndefinedNameError: reference to undefined name 'S' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[7], line 1, column 1

UndefinedNameError: reference to undefined name 'gen' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[8], line 1, column 1

\ \ \ \ \ \ ({\dot

UndefinedNameError: reference to undefined name 'S' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[9], line 1, column 1

UndefinedNameError: reference to undefined name 'gen' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[1]/span[10], line 1, column 1

\ge 0)\]

For steady-state, steady-flow devices, 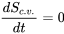$\dfrac{{dS}_{c.v.}}{dt}=0$ ; therefore,

\[\displaystyle \sum

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[1], line 1, column 1

-\sum

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[2], line 1, column 1

=\displaystyle \sum\dfrac

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[3], line 1, column 1

UndefinedNameError: reference to undefined name 'T' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[4], line 1, column 1

+{\dot

UndefinedNameError: reference to undefined name 'S' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[5], line 1, column 1

UndefinedNameError: reference to undefined name 'gen' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[6], line 1, column 1

\ \ \ \ \ \ ({\dot

UndefinedNameError: reference to undefined name 'S' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[7], line 1, column 1

UndefinedNameError: reference to undefined name 'gen' (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[1]/span[8], line 1, column 1

\ge 0)\]

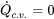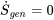For steady and isentropic flow devices, $\dot{Q}_{c.v.}=0$ and $\dot S_{gen}=0$ ; therefore,

\[\displaystyle\sum

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[2]/span[1], line 1, column 1

=\displaystyle\sum

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/div[4]/p[2]/span[2], line 1, column 1

where

\[\dot{m}\]

\[\dot{Q}_{c.v.}\]

\[S_{c.v.}\]

\[\dfrac

ParseError: EOF expected (click for details)

Callstack:
    at (Bookshelves/Mechanical_Engineering/Introduction_to_Engineering_Thermodynamics_(Yan)/06:_Entropy_and_the_Second_Law_of_Thermodynamics/6.10:_The_second_law_of_thermodynamics_for_open_systems), /content/body/p[6]/span, line 1, column 3

{dt}\]

\[\dot S_{gen}\]

\[s\]

\[T\]

Figure 6.9.1 *Flow through a control volume, showing the entropy transfers and entropy generation*

Example 1

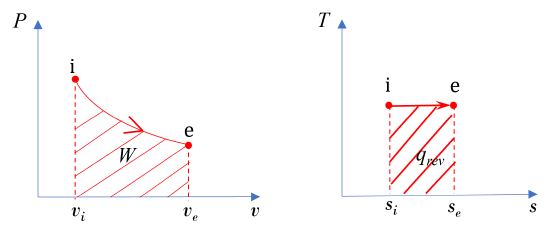
The diagrams in Figure 6.9.e1 show a reversible process in a steady-state, single flow of air. The letters i and e represent the initial and final states, respectively. Treat air as an ideal gas and assume ΔKE=ΔPE=0. Are the change in specific enthalpy Δh=h_e−h_i, specific work w, and specific heat transferq positive, zero, or negative values? What is the relation between w and q?

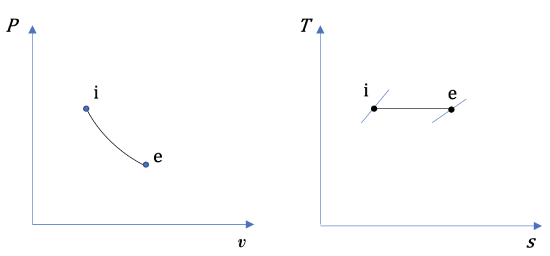
Figure 6.9.e1 T-s and P-v diagrams of a reversible process for an ideal gas

Solution:

The specific work can be evaluated mathematically and graphically.

(1) Mathematically,

\[\because v_{e} > v_{i}\]

\[\therefore w = \displaystyle\int_{i}^{e}{Pd{v}\ } >\ 0\]

(2) Graphically, the specific work is the area under the process curve in the 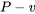$P-v$ diagram; therefore 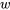$w$ is positive, see Figure 6.9.e2.

In a similar fashion, the specific heat transfer can also be evaluated graphically and mathematically.

(1) Graphically,

\[\because ds=\left(\displaystyle\frac{\delta q}{T}\right)_{rev}\]

\[\therefore q_{rev} = \displaystyle \int_{i}^{e}{Tds} = T(s_e-s_i)\ >\ 0\]

For a reversible process, the area under the process curve in the 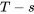$T-s$ diagram represents the specific heat transfer of the reversible process; therefore 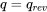$q=q_{rev}$ is positive, see Figure 6.9.e2.

(2) The same conclusion, $q_{rev}$ 0" class="latex mathjax" title="q_{rev}>0" src="/@api/deki/files/59236/d00f283ba44c47860e35c0b010cd6fb7.png">, can also be derived from the second law of thermodynamics mathematically, as follows.

\[\dot{m}(s_e-s_i)=\displaystyle\sum\frac{\dot{Q}}{T_{surr}}+\dot{S}_{gen}\]

For a reversible process, 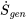$\dot{S}_{gen}$ = 0, and the fluid is assumed to be always in thermal equilibrium with the system boundary, or 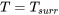$T = T_{surr}$ ; therefore,

\[q_{rev} = \dfrac{\dot{Q}}{\dot{m}} = T(s_e-s_i) > 0\]

The change in specific enthalpy can then be evaluated. For an ideal gas,

\[\Delta h = h_e - h_i = C_p(T_e - T_i)\]

\[\because T_e = T_i\]

\[\therefore h_e = h_i\]

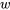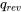Now, we can determine the relation between $w$ and $q_{rev}$ from the first law of thermodynamics for control volumes.

\[\because \dot{m}( h_e - h_i ) = \dot{Q}_{rev} - \dot{W} = 0\]

\[\therefore \dot{Q}_{rev} = \dot{W}\]

\[\therefore q_{rev} = w\]

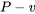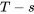In this reversible process, the specific heat transfer and specific work must be the same. Graphically, the two areas under the $P-v$ and $T-s$ diagrams must be the same.

T-s and P-v diagrams, showing the solutions for a reversible process for an ideal gas — Figure 6.9.e2 T-s and P-v diagrams, showing the solutions for a reversible process of an ideal gas

Query $\PageIndex{1}$

Media Attributions