3.1: Moment of a Force about a Point (Scalar Calculation)

Last updated
Save as PDF

Page ID: 50579

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The moment of a force is the tendency of some forces to cause rotation. Any easy way to visualize the concept is set a box on smooth surface. If you were to apply a force to the center of the box, it would simply slide across the surface without rotating. If you were instead to push on one side of the box, it will start rotating as it moves. Even though the forces have the same magnitude and the same direction, they cause different reactions. This is because the off-center force has a different point of application, and exerts a moment about the center of the box, whereas the force on the center of the box does not exert a moment about the box's center point.

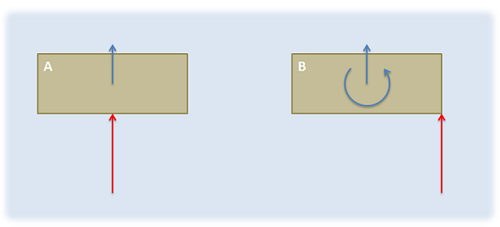
The left side of a graphic shows a box being slid across a surface by pushing against the midpoint of one of its sides. The right side shows the same box being rotated, as well as slid forward, by pushing against one of its corners. — Figure \(\PageIndex{1}\): If we push a box in the center, it will simply begin sliding. If we push a box off-center, we will exert a moment and the box will rotate in addition to sliding.

Just like forces, moments have a magnitude (the degree of rotation it would cause) and a direction (the axis the body would rotate about). Determining the magnitude and direction of these moments about a given point is an important step in the analysis of rigid body systems (bodies that are both rigid and not experiencing concurrent forces). The scalar method below is the easiest way to do this in simple two-dimensional problems, while the alternative vector methods, which will be covered later, work best for more complex three-dimensional systems.

The Scalar Method in 2 Dimensions

In discussing how to calculate the moment of a force about a point via scalar quantities, we will begin with the example of a force on a simple lever as shown below. In this simple lever there is a force on the end of the lever, distance \(d\) away from the center of rotation for the lever (point A) where the force has a magnitude \(F\).

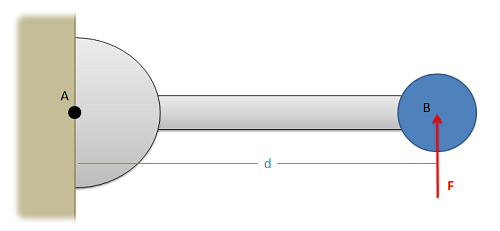
Drawing of a joystick mounted on a vertical wall, with the shaft fully perpendicular to the wall. There is a distance d between the wall's point of contact with the joystick (point A) and the center of mass of the spherical end of the joystick (point B); an upward force of magnitude F is applied at point B. — Figure \(\PageIndex{2}\): The magnitude of the moment that force \(F\) exerts about point A on this lever will be equal to the magnitude of the force times distance \(d\).

When using scalar quantities, the magnitude of the moment will be equal to the perpendicular distance between the line of action of the force and the point we are taking the moment about. \[ M \, = \, F * d \]

To determine the sign of the moment, we determine what type of rotation the force would cause. In this case, we can see that the force would cause the lever to rotate counterclockwise about point A. Counterclockwise rotations are caused by positive moments while clockwise rotations are caused by negative moments.

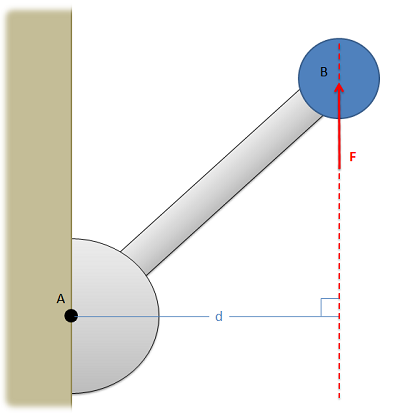
Another important factor to remember is that the value \(d\) is the perpendicular distance from the force to the point we are taking the moment about. We could measure the distance from point A to the head of the force vector, or the tail of the force vector, or really any point along the line of action of force \(F\). The distance we need to use for the scalar moment calculation, however, is the shortest distance between the point and the line of action of the force. This will always be a line perpendicular to the line of action of the force, going to the point about which we are taking the moment.

The same joystick from the previous figure is shown with point B pushed considerably forwards from its original point. The distance d is now the shortest distance connecting point A to the line extended from both ends of the vector of applied force. — Figure \(\PageIndex{3}\): Distance \(d\) always needs to be the shortest length between the line of action of the force and the point we are taking the moment about. This distance will be perpendicular to the line of action of the force.

The Scalar Model in 3 Dimensions

For three-dimensional scalar calculations, we will still find the magnitude of the moment in the same way, multiplying the magnitude of the force by the perpendicular distance between the point and the line of action of the force. This perpendicular distance again is the minimum distance between the point and the line of action of the force. In some cases, finding this distance may be very difficult.

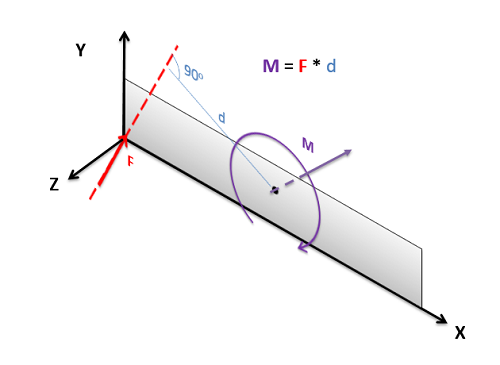
A two-dimensional rectangle, drawn on a three-dimensional coordinate plane and occupying the xy plane. A force F is applied to its left bottom corner, pushing to the left and back. A point about which the moment is being calculated is marked halfway down the rectangle's length, with distance d marked as the length of the line segment perpendicularly connecting this point to F's line of action. — Figure \(\PageIndex{4}\): For moments in three dimensions, the moment vector will always be perpendicular to both the force vector \(\vec{F}\) and the distance vector \(\vec{d}\).

Another difficult factor in three dimensional scalar problems is finding the axis of rotation, as this is now more complex that just "clockwise or counterclockwise". The axis of rotation will be a line traveling though the point about which we are taking the moment, and perpendicular to both the force vector and the perpendicular displacement vector (the vector going from the point about which the moment was taken to the point of application of the force). While this is possible in any situation, it becomes very difficult if the force or displacement vectors do not lie in one of the three coordinate directions.

To further find the direction of the moment vector (which will act along the established line for axis of rotation), we will use the right-hand rule in a modified form. Wrap the fingers of your right hand around the axis of rotation line with your fingertips curling in the direction the body would rotate. If you do this, your thumb should point out along the line in the direction of the moment vector. This is an important last step, because we can rotate clockwise or counterclockwise in about any given axis of rotation. With the final moment vector, we known not only the axis of rotation, but which way the body would rotate about that axis.

Drawing of a person's right hand, curled in demonstration of the right-hand rule as it applies to rotation. — Figure \(\PageIndex{5}\): To use the right-hand rule, align your right hand as shown so that your thumb lines up with the axis of rotation for the moment and your curled fingers point in the direction of rotation for your moment. If you do this, your thumb will be pointing in the direction of the moment vector. Adapted from Public Domain image by Schorschi2.

Video lecture covering this section, delivered by Dr. Jacob Moore. YouTube source: https://youtu.be/15h8bIQDjGE.

Example \(\PageIndex{1}\)

What is the moment that Force A exerts about point A? What is the moment that Force B exerts about Point A?

A 2-meter-long, uniformly thin lever has its base, point A, attached to a wall. The free end has two forces applied to it: A with a magnitude of 100 N straight down, B with a magnitude of 200 N pointing up and to the left, making a 30-degree angle with the horizontal. — Figure \(\PageIndex{6}\): problem diagram for Example \(\PageIndex{1}\); a lever is attached to a wall with two forces exerted upon the lever's free end.

Solution: Video \(\PageIndex{7}\): Worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/E9Xq1fXdcyE.

Example \(\PageIndex{2}\)

What is the moment that this force exerts about point A? What is the moment this force exerts about point B?

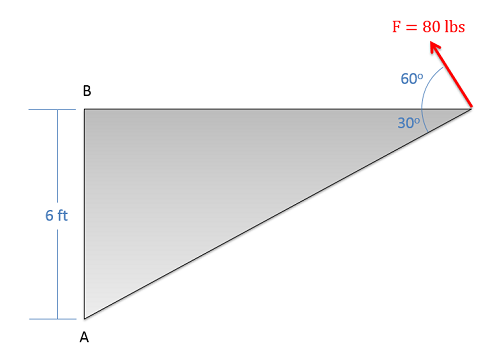
A right triangle with point B, the intersection of the two legs, at the top left corner and point A, the intersection of the hypotenuse and shorter leg, 6 feet directly below B. At the top right corner of the triangle and perpendicular to the hypotenuse, a force with magnitude 80 lbs points up and to the left, making a 60-degree angle above the horizontal. — Figure \(\PageIndex{2}\): problem diagram for Example \(\PageIndex{2}\); a force is exerted upon one corner of a right triangle.

Solution: Video \(\PageIndex{3}\): Worked solution to example problem \(\PageIndex{2}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/9nb2q3EN5gs.

Example \(\PageIndex{3}\)

What are the moments that each of the three tension forces exert about point A (the point where the beams come together)?

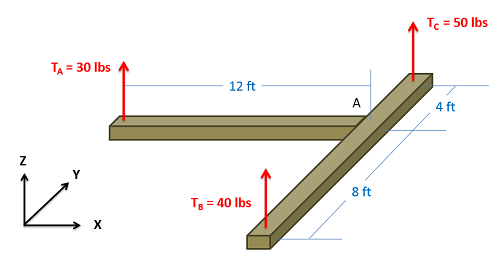
Two beams, each 12 feet long, are lying on the floor. One lies horizontally, intersecting the other beam, which lies vertically, 4 feet from one end of that vertical beam. The free end of the horizontal beam experiences an upward tension force, A, of 30 lbs; the end of the vertical beam further from the intersection point experiences an upward tension force, B, of 40 lbs; the end of the vertical beam closer to the intersection experiences an upward tension force, C, of 50 lbs. — Figure \(\PageIndex{8}\): problem diagram for Example \(\PageIndex{3}\); three tension forces are exerted on the free ends of two beams that lie perpendicular to each other.

Solution: Video \(\PageIndex{4}\): Worked solution to example problem \(\PageIndex{3}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/2W9-K2KsTMU.