Skip to main content
Engineering LibreTexts

3.7: Chapter 3 Homework Problems

  1. Last updated
  2. Save as PDF
  • Page ID
    52384

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Exercise \(\PageIndex{1}\)

    An 18-inch shelf is supported by a pin joint at point A, and a cable at point B. The shelf itself has a weight of 60 lbs. If we want the net moment about point A to be zero, what should the tension in the cable be?

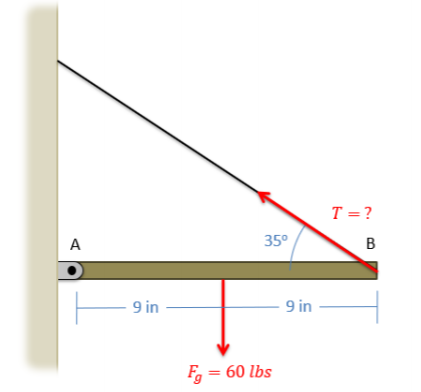    A horizontal shelf 18 inches long and weighing 60 lbs is attached to a wall with a pin joint at one end, with this point of attachment being marked A, and with a cable at the other end (point B). The cable makes a 35 degree angle with the horizontal.
    Figure \(\PageIndex{1}\): problem diagram for Exercise \(\PageIndex{1}\); a horizontal shelf is attached to a wall with a pin joint at one end and a cable at the other end.
    Solution

    \(T = 52.30 \, lbs\)

    Exercise \(\PageIndex{2}\)

    What is the moment the force shown below exerts about Point A? About Point B?

    Hint: use Varginon's Theorem.

    Top-down view of a rectangular slab, dimensions 4 by 2 meters, attached to a wall at two points along one of the long sides: A on the left edge, B on the right edge. Across from point A, a force of magnitude 6 kN is applied downwards (towards the bottom of the picture) and to the right, making a 25-degree angle below the horizontal.
    Figure \(\PageIndex{2}\): problem diagram for Exercies \(\PageIndex{2}\); a rectangular slab is bolted to a wall at two points, A and B, with a force is exerted on one of the rectangle's unattached corners.
    Solution

    \(M_A = 10.88 \, kNm \)

    \(M_B = 21.02 \, kNm\)

    Exercise \(\PageIndex{3}\)

    You are attempting to rotate a heavy table about the base of one leg at point O and are going to exert a 100-lb force at the opposite end. Person A recommends pulling straight up, while person B recommends pulling up at 30° from vertical. What would be the moment about point O, in inch-pounds, in either case?

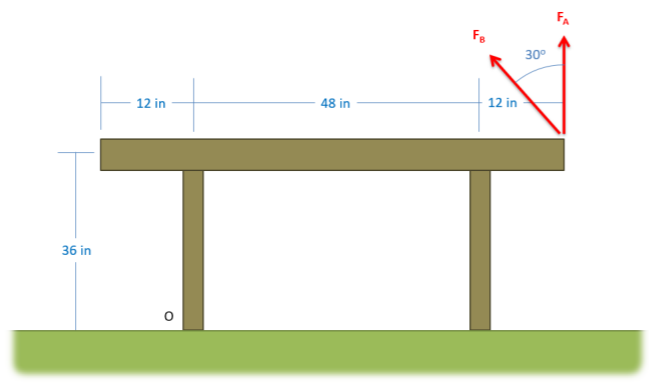    Side view of a two-legged rectangular table, 36 inches high; each leg is 12 inches from the nearest end and the legs are 48 inches apart. Point O is the point where the left leg makes contact with the ground. At the rightmost corner of the table surface, vectors for the forces A and B described in the problem are drawn in.
    Figure \(\PageIndex{3}\): problem diagram for Exercise \(\PageIndex{3}\); a table is rotated about the base of one leg, with one of the two proposed forces applied at the tabletop at the opposite end.
    Solution

    \(M_{AO} = 6000 \, \text{in-lbs} \)

    \(M_{BO} = 6996.15 \, \text{in-lbs}\)

    Exercise \(\PageIndex{4}\)

    Determine the moment vectors that each of the three tension forces in the diagram below exerts about the origin point O. Provide the answers in vector form with units.

    Two beams are laid out on the xy plane: one extends 8 meters in the positive x-direction from the origin, the other extends 6 meters in the positive y-direction and 3 meters in the negative y-direction. Three upward forces are applied at the ends of the beams: A, with magnitude 50 N, at the free end of the beam along the x-axis; B, with magnitude 100 N, at the end of the beam in the negative y direction; C, with magnitude 50 N, at the end of the beam in the positive y direction.
    Figure \(\PageIndex{4}\): problem diagram for Exercise \(\PageIndex{4}\); two straight beams lying in the \(xy\)-plane, joined perpendicularly to each other, experience 3 upward tension forces (in the +\(z\) direction).
    Solution

    \(M_{AO} = [0, \, -400, \, 0] \, Nm\)

    \(M_{BO} = [-300, \, 0, \, 0] \, Nm\)

    \( M_{CO} = [300, \, 0, \, 0] Nm\)

    Exercise \(\PageIndex{5}\)

    You exert a 50-lb force on the side of a fridge as shown below. Assuming the fridge is sitting on a rough surface and not moving, what is the magnitude of the moment exerted by the couple consisting of the pushing force and the friction force?

    A refrigerator, 3 feet wide and with a center of mass 3 feet above the midpoint of the width, sits on a flat surface. A horizontal force of 50 N towards the right is applied to the left side of the fridge, 2 feet above the ground.
    Figure \(\PageIndex{5}\): problem diagram for Exercise \(\PageIndex{5}\); a force is exerted on a refrigerator that sits on a flat surface, without causing it to move.
    Solution

    \(M = -100 \text{ft-lbs}\)

    Exercise \(\PageIndex{6}\)

    A space station consists of a large ring that spins in order to provide an artificial gravity for the astronauts in the station. To start the station spinning, a pair of thrusters is attached to the outside of the ring, each pointing in opposite directions as shown below.

    a) If we want to exert a 10 kN-m moment with the thrusters, and the ring has a diameter of 45 meters, what thrust force should each thruster produce?

    b) If we were to use the same thrusters on a 60-meter diameter ring, what moment would they exert?

    A space station in the shape of a large ring connected to a central hub. A ring of uniform inner and outer diameter with one thruster force located on the rightmost point of the outer diameter, pointing upwards, and another thruster force located directly opposite pointing downwards, producing a counterclockwise rotation of the ring.
    Figure \(\PageIndex{6}\): problem diagram for Exercise \(\PageIndex{6}\). An example of the spinning ring-shaped space station as described in the problem (left); a diagram of the locations and directions of the thruster forces on the ring (right).
    Solution

    a) \(F_{thruster} = 222.22 \, N\)

    b) \(M_{thruster} = 13.33 \, kNm\)

    Exercise \(\PageIndex{7}\)

    A 60-N force is applied in the \(yz\) plane, 40° from the \(y\) direction, on an L-shaped bar as shown below.

    a) What is the moment vector this force exerts about point O?

    b) What is the overall magnitude of the moment about point O?

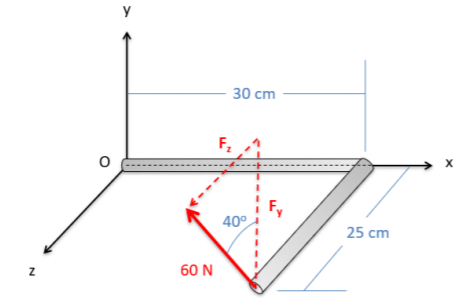    An L-shaped bar in the xz plane, with one horizontal 30-cm segment starting at the origin (point O) and extending along the positive x-axis and the other 25-cm segment pointing out of the screen in the z-direction. A force of magnitude 60 N is exerted on the free end of the 25-cm segment, pointing left and into the screen (making a 40-degree angle with the vertical, or the y-direction).
    Figure \(\PageIndex{7}\): problem diagram for Exercise \(\PageIndex{7}\); an L-shaped bar lies in the \(xz\) plane with one end located at the origin, point O, and the other experiencing a force in the \(yz\) direction.
    Solution

    \(M_O = [-11.49, \, -11.57, \, 13.79] \, Nm\)

    \(|M| = 21.36 \, Nm\)

    Exercise \(\PageIndex{8}\)

    What is the moment that the force shown in the diagram exerts about point O? About the axis of the cylindrical shaft (the \(y\)-axis)?

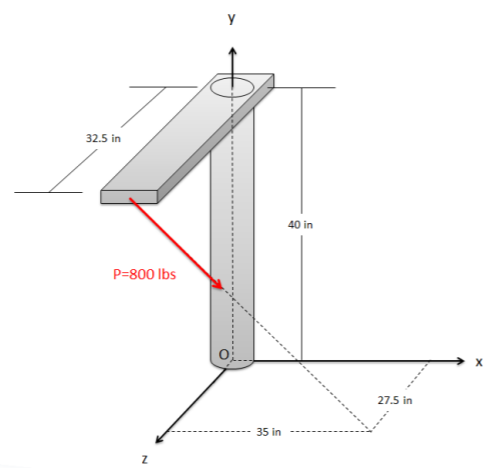    A 40-inch-long cylinder with a central axis lying along the vertical y-axis has one end at the origin (point O) and the other end attached to a rectangular bar 32.5 inches long, pointing out of the screen in the z direction. A force P is applied to the free end of the bar, with magnitude 800 lbs; the line of action of P intersects the xz plane at the point (27.5, 0, 35) in.
    Figure \(\PageIndex{8}\): problem diagram for Exercise \(\PageIndex{8}\); an L-shaped part that extends in the \(y\) and \(z\) directions, with one end located at the origin O, experiences a force in the \(xz\) direction applied at the opposite end.
    Solution

    \(M_O = [16484, \, 17046, \, -20979] \, in-lbs\)

    \(M_y = 17046 \, in-lbs\)

    Exercise \(\PageIndex{9}\)

    The diving board shown below is supported by a pin joint at A and frictionless support at B. A 150-lb diver is standing at the end of the board. Determine the reaction forces acting on the diving board at points A and B.

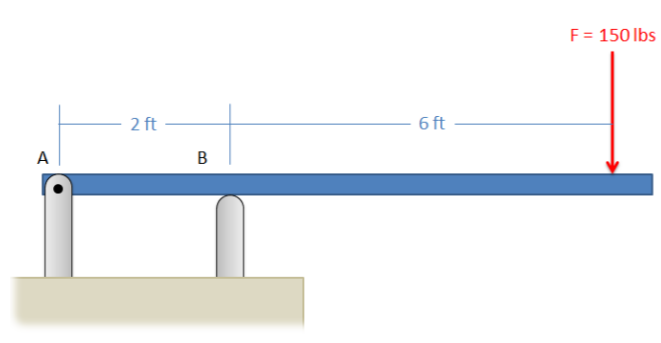    An 8-foot-long diving board extends to the right; its leftmost edge, point A, is supported with a pin joint and point B, 2 feet to the right, is supported by a frictionless support. A weight of 150 lbs is applied to the right end of the board.
    Figure \(\PageIndex{9}\): problem diagram for Exercise \(\PageIndex{9}\); a diving board is supported by a pin joint at its leftmost end (point A) and a frictionless support two feet to the right (point B), with a 150-lb diver standing 6 feet to the right of B.
    Solution

    \(F_{AX} = 0\)

    \(F_{AY} = -450 \, lbs\)

    \(F_{BY} = 600 \, lbs\)

    Exercise \(\PageIndex{10}\)

    A simplified crane is shown lifting a 400-kg load. The crane is supported by a pin joint at A, and a cable at B. Assuming the crane arm is in equilibrium, what are the reaction forces at A and the tension at B?

    A 10-meter-long crane arm stretches up and to the right, 40 degrees above the horizontal. The left end, point A, is attached to a vertical support; the beam's midpoint, point B, is attached to a horiztonal cable that stretches left; and a 400-kg block hangs from the right end of the beam.
    Figure \(\PageIndex{10}\): problem diagram for Exercise \(\PageIndex{10}\); a crane arm is attached to a vertical support at one end (A), is connected to a horizontal cable at its midpoint (B), and lifts at a 400-kg load at the other end.
    Solution

    \(F_{AX} = 9352.9 \, N\)

    \(F_{AY} = 3924 \, N\)

    \(T_{B} = 9352.9 \, N\)

    Exercise \(\PageIndex{11}\)

    An 8-foot ladder sits propped up against a wall at a 60-degree angle as shown below. It has a weight of 50 lbs acting at its center point and supports a 120-lb woman 6 feet from the bottom. Assume that friction acts at the bottom of the ladder, but not the top. What are the normal forces acting at the bottom and top of the ladder, and what is the friction force acting at the bottom of the ladder?

    An 8-foot-long ladder is propped against a wall, making a 60-degree angle with the floor. A gravitational force of 50 lbs acts on the ladder at its midpoint, and a woman with a weight of 120 lbs stands on the ladder at the point 6 feet away from the ladder's point of contact with the floor.
    Figure \(\PageIndex{11}\): problem diagram for Exercise \(\PageIndex{11}\); an 8-ft ladder weighing 50 lbs and supporting a 120-lb woman who has climbed 75% of the way up leans, at 60° above the horizontal, against a wall.
    Solution

    \(F_{N \, Top} = 66.4 \, lbs\)

    \(F_{N \, Bottom} = 170 \, lbs\)

    \(F_f = 66.4 lbs\)

    Exercise \(\PageIndex{12}\)

    An SUV with a weight of 4200 lbs and a center of mass located as shown below is parked pointed downhill on a 10-degree incline. The parking is engaged, locking up the back wheels but not the front wheels. What is the expected normal force at the front wheels, the expected normal force at the back wheels, and the expected friction force at the back wheels assuming the SUV does not slip?

    An SUV is parked pointing downhill on a 10-degree incline. There is a distance of 6 feet between the centers of the front and rear wheels; the SUV's center of gravity is marked as located 2 feet behind the center of the front wheel and 2 feet above the plane of the incline.
    Figure \(\PageIndex{12}\): problem diagram for Exercise \(\PageIndex{12}\); an SUV with front and rear wheels 6 feet apart, and a center of mass 2 feet above the ground and 2 feet behind the front wheel, is parked pointing downhill on a 10° incline.
    Solution

    \(F_f = 729.3 \, lbs\)

    \(F_{N \, front} = 3000.6 \, lbs\)

    \(F_{N \, back} = 1135.6 \, lbs\)

    Exercise \(\PageIndex{13}\)

    A cart with a mass of 3500 kg sits on an inclined surface as shown below. Determine the reaction forces acting on each wheel of the cart as well as the tension in the cable supporting the cart.

    A cart sits facing uphill on a 30-degree incline, with two wheels A (rear) and B (front) 4 meters apart. A cable is attached to the front of the cart, 1 meter in front of wheel B and 2.5 meters above the plane of the incline, making a 38-degree angle with the incline. The cart's center of mass is midway between wheels A and B, 1.5 meters above the plane of the incline.
    Figure \(\PageIndex{13}\): a two-wheeled cart is parked facing uphill on a 30° slope. A cable stretches from the front of the cart to a support on the incline, making a 38° angle with the plane of the incline.
    Solution

    \(T = 21786 \, N\)

    \(F_A = 7222 \, N; \, F_B = 35925 \, N\)

    Exercise \(\PageIndex{14}\)

    The lighting rig above a stage consists of two 100-lb, uniform beams joined together in a T as shown below (assume the weight acts in the center of each beam). The rig is supported by three cables at A, B, and C. Determine the tension in each of the three cables.

    Two 12-foot beams are attached perpendicularly to each other, lying in the xy plane. One lies horizontally, with a cable attached at its left end (point A). Cable B attaches to one end of the second beam, 8 feet away from the point of intersection with the horizontal beam, and cable C attaches to the other end of the second beam.
    Figure \(\PageIndex{14}\): problem diagram for Exercise \(\PageIndex{14}\); two beams attached perpendicularly to each other lie in the \(xy\) plane in a T shape experience upward tension forces from 3 cables, one attached to each free end of the T.
    Solution

    \(T_A = 50 \, lbs; \, \, T_B = 66.7 \, lbs; \, T_C = 83.3 \, lbs\)

    Exercise \(\PageIndex{15}\)

    A 9-meter-long pole with a mass of 100 kg is suspended horizontally, 4 meters from the ceiling with three cables as shown below. Assuming the center of mass of the pole is at the center point of the pole, what is the expected tension in each of the three cables?

    A 9-meter-long pole, aligned with the x-axis, is suspended from the ceiling by 3 cables. Cables A and B attach to the pole at 2 meters from one end, each attaching to the ceiling at a location 3 meters from the x-axis (in the z-direction, pointing into and out of the page). Cable C attaches to the pole 6 meters away from the point where A and B attach, and hangs vertically at a length of 4 meters.
    Figure \(\PageIndex{15}\): problem diagram for Exercise \(\PageIndex{15}\); a pole hangs 4 meters below the ceiling, suspended by 3 cables attached to the pole at different locations and angles.
    Solution

    \(T_A = 357.66 \, N; \, T_B = 357.66 \, N; \, T_C = 408.75 \, N\)

    This page titled 3.7: Chapter 3 Homework Problems is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.