6.2: Dislocation Basis of Yield and Creep
- Page ID
- 44551
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Phenomenological treatments such those outlined in the Module on Yield and Plastic Flow (Module 20) are very useful for engineering predictions, but they provide only limited insight to the molecular mechanisms underlying yield. Molecular understanding is a higher level of insight, and also guides processing adjustments that can optimize the material. As discussed in the Module on Atomistics of Elasticity (Module 2), the high level of order present in crystalline materials lead to good atomistic models for the stiffness. Early workers naturally sought an atomistic treatment of the yield process as well. This turned out to be a much more subtle problem than might have been anticipated, and required hypothesizing a type of crystalline defect — the "dislocation" — to explain the experimentally observed results. Dislocation theory permits a valuable intuitive understanding of yielding in crystalline materials, and explains how yielding can be controlled by alloying and heat treatment. It is one of the principal triumphs of the last century of materials science.
Theoretical yield strength
In yield, atoms slide tangentially from one equilibrium position to another. The forces required to bring this about are given by the bond energy function, which is the anharmonic curve resulting from the balance of attractive and repulsive atomic forces described in Module 2. The force needed to displace the atom from equilibrium is the derivative of the energy function, being zero at the equilibrium position (Figure 1). As a simplifying assumption, let us approximate the force function with a harmonic expression, and write
\(\tau = \tau_{\max} \sin (2\pi \dfrac{x}{a})\)
where \(a\) is the interatomic spacing. The stress reaches a maximum a quarter of the distance between the two positions, dropping to zero at the metastable position midway between them. After that, the stress changes sign, meaning that force is required to hold the atom back as it tries to fall toward the new equilibrium position. Using \(\gamma = x/a\) as the shear strain, the maximum shear stress \(τ_{max}\) can be related to the shear modulus \(G\) as
\(\dfrac{d\tau}{d\gamma} = \dfrac{d\tau}{dx}\dfrac{dx}{d\gamma} = a \dfrac{d\tau}{dx} = a \tau_{\max} \dfrac{2\pi}{a} \cos \dfrac{2\pi x}{a}\)

\(G = \dfrac{d\tau}{d\gamma}|_{\gamma \to 0} = \tau_{\max} \cdot 2 \pi\)
This implies a shear stress at yield of \(\tau_{\max} = G/2\pi \approx G/10\), which would be on the order of 10 GPa. Measured values are 10–100 MPa, so the theoretical value is 2 to 3 orders of magnitude too large. More elaborate derivations give a somewhat smaller value for the theoretical yield stress, but still much larger than what is observed experimentally.
Edge, screw, and mixed dislocations
A rationale for the apparently low experimental values for the yield strengths of crystalline materials was proposed independently by Taylor, Polyani and Orowan in 1934. These workers realized that it was not necessary to slip entire planes of atoms past one another to deform the material plastically, a process that would require breaking all the bonds connecting the planes simultaneously. The stress needed to do this would be very high, on the order of \(G/10\) as described above. But it isn’t necessary to move all the atoms at once; only a few at a time need to move, requiring a much smaller stress. Analogously to the way an inchworm moves, only those atoms lying in a plane above a single line might be displaced one atomic spacing. This would force the plane of atoms previously there into a midway position as shown in Figure 2, creating an "extra" plane of atoms halfway between the normal equilibrium positions. The termination of this plane then constitutes a line defect in the crystal known as a dislocation(For an extended discussion of the geometrical aspects of crystal dislocations, see S.M. Allen and E.L. Thomas, The Structure of Materials, John Wiley & Sons, New York, 1999.).
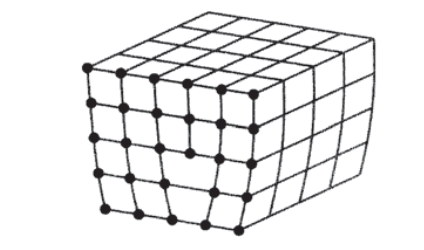
Viewed end-on as seen in Figure 3, it can be appreciated that the extra plane of atoms creates a region of compression near the plane but above the dislocation line, and a tensile region below it. In a "soft" crystal whose interatomic bonds are relatively compliant, the distortion extends an appreciable distance from the dislocation. Conversely, in "hard" crystals with stiffer bonds the distortion is confined to a smaller region near the dislocation. The face-centered cubic (fcc) metals such as copper and gold have close-packed planes (those with (111) Miller indices), which corresponds to large distances between those planes. This gives rise to relatively soft interplanar bonds, so that the dislocation width is large. The dislocation width is substantially smaller in the body centered cubic (bcc) metals such as iron and steel, smaller still in ionically bonded ceramics, and even smaller in covalently bonded ceramics.

The dislocation associated with this extra plane of atoms can be moved easily, since only a small adjustment in position is required to break the bonds on the next plane over and allow them to form on the originally "extra" plane. Now the third plane is the extra one, and the dislocation will have moved by one atomic position. Slip is obviously made much easier if dislocation motion is available to the material. In fact, it first appears the dislocation concept does too good a job in explaining crystal plasticity, since the dislocation is in a balanced metastable position and should be capable of being moved either left or right with a vanishingly small force. If this were true, the crystal would have essentially no shear strength.
However, as the dislocation moves it drags with it the regions of compressive and tensile distortion in the lattice around it. This is accompanied by a sort of frictional drag, giving rise to a resistance to dislocation motion known as the Peierls force. This force is dependent on such factors as the crystal type and the temperature, and this plays an important role in determining the material’s yield stress. As seen in Table 1, materials with wide dislocations have low Peierls forces, since the distortion is spread out over a large volume and is much less intense at its core.
Table 1 also indicates that the effect of temperature on the Peierls force is low for fcc materials having wide dislocations, and this results in a small temperature dependency of the yield stress. Conversely, materials with narrow and intense dislocation fields have high Peierls forces with a large temperature sensitivity of the yield stress, with higher temperatures facilitating dislocation mobility and thus reducing the yield strength. Among the important consequences of these factors is the dangerous tendency of steel to become brittle at low temperatures; as the temperature is lowered, the yield stress can rise to such high levels that brittle fracture intervenes.
| Material | Crystal Type | Dislocation Width | Peierls Stress | Yield Strength Temperature Sensitivity |
|---|---|---|---|---|
| Metal | fcc | wide | very small | negligible |
| Metal | bcc | narrow | moderate | strong |
| Ceramic | ionic | narrow | large | strong |
| Ceramic | covalent | very narrow | very large | strong |
Dislocations can have geometries other than the simple edge dislocation shown in Figure 3. A more general view is provided by considering displacing a portion of the atoms in a "slip plane" \(acfg\) a distance \(\bar{b}\), as shown in Figure 4. The vector \(\bar{b}\) is also a measure of the magnitude and direction of the crystal dislocation, and is known as the Burgers’ vector. The boundary between slipped and unslipped atoms on the slip plane is the dislocation line, shown as a dotted line. At position \(e\), the dislocation line is perpendicular to the Burgers’ vector, so these two quantities lie in the slip plane. A dislocation so situated is called an edge dislocation, and is constrained to move only in the slip plane defined by the dislocation line and the Burgers’ vector.

At position \(b\), a spiral-like defect is formed such that a circular transit around the dislocation line ends on a plane a distance \(\bar{b}\) from the starting point. Now the defect is known as a screw dislocation. The dislocation line is now parallel to the Burgers’ vector, so these two quantities do not define a unique slip plane the way an edge dislocation does. A screw dislocation can therefore cross-slip to another easy-glide plane passing through the dislocation line, and this mechanism enables screw dislocations to maneuver around obstacles that might otherwise impede their motion. Edge dislocations are more easily pinned, since they must "climb" by diffusion of vacancies to surmount obstacles as illustrated in Figure 5.
As the curved dislocation line is traversed from point \(b\) to point \(e\), the dislocation changes gradually from screw to edge character. At intermediate points the dislocation has both edge and screw character, and is known as a mixed dislocation.

Dislocation-controlled yield
Single crystals tend to slip on their most closely packed planes, and in directions of minimum atomic separation distance. The distances between planes is maximum for the close-packed planes, so these are the most loosely bonded. Slip in close-packed directions minimizes the distance the stresses need to displace the slipping atoms. Both of these act to minimize the energy needed for slip. There are 12 such slip systems in the face-centered cubic (fcc) systems; using Miller indices, these are the {111} planes and the \(\langle 110 \rangle\) directions. There are 4 independent nonparallel (111) planes, and 3 independent [110] directions in each plane.
| Material | crystal type | slip system | \(\tau_{crss}\), MPa |
|---|---|---|---|
| Nickel | fcc | {111} \(\langle 110 \rangle\) | 5.7 |
| Copper | fcc | {111} \(\langle 110 \rangle\) | 0.98 |
| Gold | fcc | {111} \(\langle 110 \rangle\) | 0.90 |
| Silver | fcc | {111} \(\langle 110 \rangle\) | 0.60 |
| Magnesium | hcp | {1101} \(\langle 001 \rangle\) | 0.81 |
| NaCl | cubic | {110} \(\langle 110 \rangle\) | 0.75 |
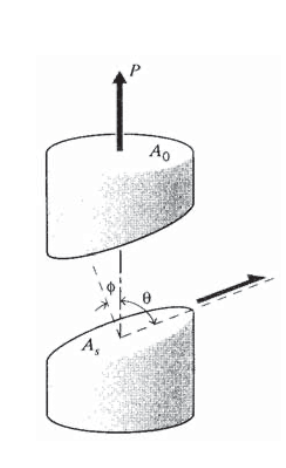
Slip occurs when the shear stress on the slip plane, and in the slip direction, reaches a value \(\tau_{crss}\), the critical resolved shear stress; experimental values for \(\tau_{crss}\) are listed in Table 2 for a number of single crystal materials. The resolved shear stress corresponding to an arbitrary stress state can be computed using the transformation relations of Module 10. In a simple tension test it can be written by inspection of Figure 6 as
\(\tau_{rss} = \dfrac{P \cos \theta}{A_s} = \dfrac{P \cos \theta}{A_0/\cos \phi} = \sigma (\cos \theta \cos \phi) \equiv \dfrac{\sigma}{m}\)
where \(m\) is a structure factor dependent on the orientation of the slip system relative to the applied tensile stress. For single crystals of arbitrary alignment, the yield stress will then be of the form
\[\sigma_Y = \tau_{crss} \cdot m\]
This is known as “Schmid’s Law,” and \(m\) is the “Schmid factor.”
The yield stress will generally be higher in polycrystalline materials, since many of the grains will be oriented unfavorably (have high Schmid factors). Equation 6.2.1 can be modified for polycrystalline systems as
\(\sigma_Y = \tau_{crss} \cdot \bar{m}\)
where \(\bar{m}\) is an equivalent Schmid factor that is generally somewhat higher than a simple average over all the individual grains; for fcc and bcc systems \(\bar{m} \approx 3\).
Strain energy in dislocations
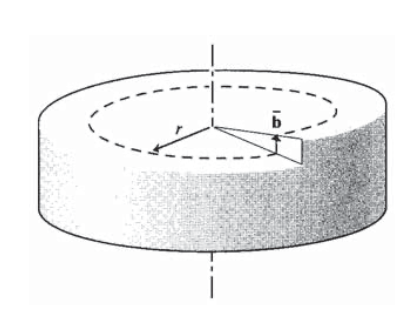
Many calculations in dislocation mechanics are done more easily with energy concepts than with Newtonian force-displacement approaches. As seen in Figure 7, the shear strain associated with a screw dislocation is the deflection \(\bar{b}\) divided by the circumference of a circular path around the dislocation core:
\[\gamma = \dfrac{\bar{b}}{2\pi r}\]
where \(r\) is the distance from the dislocation core.
Assuming Hookean elasticity, the corresponding strain energy per unit volume is
\(U = \int \tau d \gamma = \dfrac{1}{2} r \gamma = \dfrac{G\gamma^2}{2} = \dfrac{G \bar{b}^2}{8\pi^2 r^2}\)
The total strain energy associated with the screw dislocation is now obtained by integrating this over the volume around the dislocation:
\(U_{screw} = \int U\ dV = l \cdot \int_{r_0}^{r} \dfrac{G \bar{b}^2}{8\pi^2 r^2} 2 \pi r \ dr\)
where here \(l\) is the length of the dislocation line and \(r_0\) is the radius of the dislocation "core" inside which the energy is neglected. (Mathematically, the energy density increases without bound inside the core; however its volume becomes very small.) Taking \(l = 1\) to obtain energy per unit length and carrying out the integration,
\[U_{screw} = \dfrac{G \bar{b}^2}{4\pi} \ln \dfrac{r}{r_0} \approx G \bar{b}^2\]
This last approximation should be read “scales as,” since it is arbitrary to select the limiting value \(r\) so that \(\ln \dfrac{r}{r_0} \approx 4\pi\). The important conclusion is that the dislocation energy increases linearly with the shear modulus \(G\) and quadratically with the Burgers' vector \(\bar{b}\). A similar expression can be obtained for the strain energy per unit length of edge dislocation; it can be shown that
\[U_{edge} = \dfrac{G \bar{b}^2}{1 - v}\]
where \(v\) is the Poisson's ratio.
The dislocation energy represents an increase in the total energy of the system, which the material will try to eliminate if possible. For instance, two dislocations of opposite sign will be attracted to one another, since their strain fields will tend to cancel and lower the energy. Conversely, two dislocations of same sign will repel one another. The force of this attraction or repulsion will scale as
\(F\ dr = dU \Rightarrow F_{screw} \approx \dfrac{G\bar{b}^2}{r}\)
where here \(r\) is the distance between dislocations.
Dislocation motion and Hardening
The ductility of crystalline materials is determined by dislocation mobility, and factors that impede dislocation motion can produce dramatic increases in the material’s yield strength. This increased resistance to plastic flow also raises the indentation hardness of the material, so strengthening of this sort is known as hardening. Alloying elements, grain boundaries, and even dislocations themselves can provide this impediment, and these provide the means by which the materials technologist controls yield. A thorough treatment of these important concepts must be left to subjects in physical metallurgy, but the following paragraphs will provide a brief introduction to some of them.
When one dislocation, moving on its slip plane under the influence of a driving shear stress, passes through another a "jog" will be created in the second dislocation as shown in Figure 8.
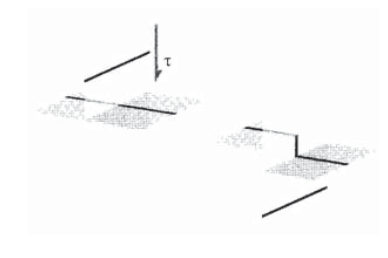
The portion of the dislocation line in the jog is now no longer on its original glide plane, and is "pinned" in position. If the dislocation concentration is large, these jogs become a powerful impediment to plastic flow by dislocation motion. Paradoxically, the very dislocations that permit plastic flow in the first place can impede it if they become too numerous.
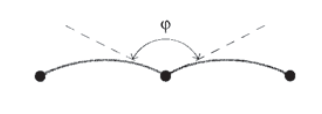
When a moving dislocation becomes pinned by jogs or other impediments, the shear stress \(\tau\) that had been driving the dislocation now causes the line segment between the obstacles to bow forward as shown in Figure 9, with an angle \(\phi\) between adjacent segments. The extra length of the bowed line represents an increase in the strain energy of the dislocation, and if the shear stress were not present the line would straighten out to reduce this energy. The line acts similarly to an elastic band, with a "line tension" \(T\) that acts to return the line to a straight shortest-distance path between pinning points. The units of dislocation energy per unit length (N-m/m) are the same as simple tension, and we can write
\(T = \dfrac{\partial E}{\partial l} \approx Gb^2\)

As shown in Figure 10, a free-body diagram of the line segment between two pinning points gives a force balance of the form
\(2 T \sin \dfrac{d \theta}{2} = r \bar{b} \cdot r \ d\theta\)
where here \(r\) is the radius of curvature of the line (not the distance from the dislocation, as in Equation 6.2.2). Rearranging and canceling the \(d \theta\) factor,
\[r = \dfrac{G \bar{b}}{r}\]
This relation gives the curvature of the dislocation in terms of the shear stress acting on it. The maximum shear stress is that needed to bend the dislocation into a semicircle (smallest \(r\)), after which the dislocation expands spontaneously. When the loops meet, annihilation occurs at that point, spawning a new dislocation line embedded in a circular loop. The process can be repeated with the new dislocation as well, and by this mechanism a large number of dislocations can be spawned as shown in Figure 11. This is the “Frank-Read” source, and is an important means by which dislocations can multiply during plastic deformation. The increasing number of dislocations leads to more and more entanglements, with jogs acting as pinning points.
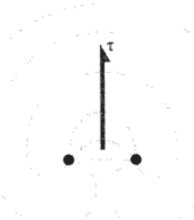
Equation 6.2.5 also provides an estimate of the influence of dislocation density on yield strength. If the obstacles pinning dislocation motion are "soft" the dislocation will be able to overcome them at relatively low driving stress, corresponding to a low critical angle \(\phi_c\). But as the obstacle becomes "harder," i.e. provides more resistance to dislocation motion, the angle approaches zero and the radius of curvature becomes on the order of the obstacle spacing \(L\). The shear stress needed to overcome such obstacles is then
\(\tau \approx \dfrac{G\bar{b}}{L}\)
When the hard obstacles arise from jogs created by intersections with other dislocations, the obstacle spacing \(L\) can be written in terms of the dislocation density. If the number of dislocations passing through a unit area is \(\rho\), the number of dislocations encountered in moving along a straight line will be proportional to \(\sqrt{\rho}\). The spacing between them is proportional to the reciprocal of this, so \(\tau \propto G\bar{b} \sqrt{\rho}\). The yield stress is then the stress \(\tau_0\) needed to move dislocations in the absence of interfering dislocations, plus that needed to break through the obstacles; this can be written as
\[\tau_{\Gamma} = \tau_0 + AG\bar{b} \sqrt{\rho}\]
where \(A\) is a constant that has been found to vary between 0.3 and 0.6 for a number of fcc, bcc and polycrystalline metals as well as some ionic crystals. Experimental corroboration of this relation is provided in Figure 12.
The action of plastic flow therefore creates new dislocations by Frank-Read and other sources, which makes the material harder and harder, i.e. increasingly resistant to further plastic flow.

Eventually the yield stress for continued deformation becomes larger than the fracture stress, and the material will now break before it deforms further. If continued working of the material is desired, the number of dislocations must be reduced, for instance by thermal annealing. Annealing can produce recovery (dislocation climb around obstacles by vacancy diffusion) or recrystallization of new dislocation-free grains.
Grain boundaries act to impede dislocation motion, since the slip systems in adjoining grains will usually not line up; increases in yield strength arising from this mechanism are called boundary strengthening. Fine-grained metals have increased grain boundary area and thus have higher yield strengths than coarse-grained ones. The influence of grain size can often be described by the Hall-Petch formula
\[\sigma_Y = \sigma_0 + k_Y d^{-1/2}\]
where \(\sigma_0\) is the lattice friction stress needed to move dislocations and \(K\) is a constant. This relation is essentially empirical, but it can be rationalized by viewing the second term as being related to the stress needed to activate a new mobile dislocation in the unfavorably oriented grain.

As dislocations pile up against the boundary in the originally deforming grain, they act much like a crack whose length scales with the grain size \(d\) as shown in Figure 13: the larger the grain, the more dislocations in the pileup, the larger the virtual crack. Since the stress in front of a sharp crack of length \(a\) scales as \(\sqrt{a}\), the stress in front of the crack containing the dislocation pileup is increased by a factor that scales with that needed to generate a new dislocation the unfavorably oriented grain begins to deform by dislocation motion. This stress diminishes according to \(d^{-1/2}\) as the size of the original grain is scaled down, thus strengthening the metal according to the Hall-Petch relationship. Grain size is determined by the balance between nucleation and growth rates as the metal is solidified, and these are in turn controllable by the cooling rates imposed. This is an important example of processing-structure-property control available to the materials technologist.
A related phenomenon accounts for the very high strengths (\(\approx\) 4 GPa, or 600 kpsi ) of piano wire, a eutectoid steel that has been drawn through a sequence of reducing dies to obtain a small final diameter. The "pearlitic" structure obtained on cooling this steel through the eutectoid temperature is a two-phase mixture of Fe\(_3\)C ("cementite") in bcc iron ("ferrite"). As the diameter is reduced during drawing, the ferrite cells are reduced as well, forming a structure analogous to a fine-grained metal. The cell boundaries restrict dislocation motion, leading to the very high yield strengths.
Impurity atoms in solid solution can also serve to harden a crystalline material by impeding dislocation motion; this is called solution strengthening. An impurity atom smaller than the atoms of the host lattice will create an approximately spherical tensile field around itself which will attract the compressive regions around mobile dislocations, and a larger impurity atom will tend to trap the tensile region of nearby dislocations. On average, the population of dislocations will maneuver so as to lower their strain energies by associating with the nonuniform strain fields around impurities. This association impedes dislocation motion, which inhibits plastic flow and increases the yield stress.
Solution hardening is not usually an especially effective strengthening mechanism in commercial materials, largely because the solubility of impurity atoms is not sufficient to generate an appreciable number of obstacles. One important exception to this is the iron-carbon, or steel, system. If steel at approximately the eutectoid carbon composition (0.8% \(C\)) is cooled rapidly from above the eutectoid temperature of 723\(^{\circ}C\), the carbon atoms can become trapped in the iron lattice at much higher concentrations than bcc iron’s equilibrium carbon solubility would normally allow. (This tendency for trapping can be enhanced by alloying elements such as chromium and molybdenum, which have an affinity for carbon and thus reduce its ability to diffuse away.) To accommodate these metastable impurity atoms, the iron lattice transforms to a body-centered tetragonal form named martensite (see Figure 14), with a strong nonspherical strain field around the carbon atoms. These tetragonal distortions are very effective impediments to dislocation motion, making martensite an extremely hard phase. The periodic water quenches a blacksmith uses during metalworking is done (perhaps without the smith knowing why it works) to tailor the material’s hardness by developing martensitic inclusions in the steel.
Martensite is so hard and brittle that the rapidly quenched steel must usually be tempered by heating it to approximately 400\(^{\circ}C\) for an hour or so. This allows diffusion of carbon to take place, creating a dispersion of cementite inclusions; it also permits recovery of the dislocations present in the martensite. The resulting material is much tougher than the as-formed martensitic steel, but still retains a high strength level due to the strengthening effect of the carbide inclusions.

Kinetics of creep in crystalline materials
“Creep” is the term used to describe the tendency of many materials to exhibit continuing deformation even though the stress is held constant. Viscoelastic polymers exhibit creep, as was discussed in Module 19. However, creep also occurs in polycrystalline metallic and ceramic systems, most importantly when the the temperature is higher than approximately half their absolute melting temperature. This high-temperature creep can occur at stresses less than the yield stress, but is related to this module’s discussion of dislocation-controlled yield since dislocation motion often underlies the creep process as well.
High-temperature creep is of concern in such applications as jet engines or nuclear reactors. This form of creep often consists of three distinct regimes as seen in Figure 15: primary creep, in which the material appears to harden so the creep rate diminishes with time; secondary or steady state creep, in which hardening and softening mechanisms appear to balance to produce a constant creep rate \(\dot{\epsilon}_{II}\); and tertiary creep in which the material softens until creep rupture occurs. The entire creep curve reflects a competition between hardening mechanisms such as dislocation pileup, and mechanisms such as dislocation climb and cross-slip which are termed recovery and which augment dislocation mobility.

In most applications the secondary regime consumes most of the time to failure, so much of the modeling effort has been directed to this stage. The secondary creep rate \(\dot{\epsilon}_{II}\) can often be described by a general nonlinear expression of the form
\[\dot{\epsilon}_{II} = A \sigma^m \exp \dfrac{-E_c^*}{RT}\]
where \(A\) and \(m\) are adjustable constants, \(E_c^*\) is an apparent activation energy for creep, \(\sigma\) is the stress, \(R\) is the Gas Constant (to be replaced by Boltzman’s constant if a molar basis is not used) and \(T\) is the absolute temperature. This is known as the Weertman-Dorn equation.
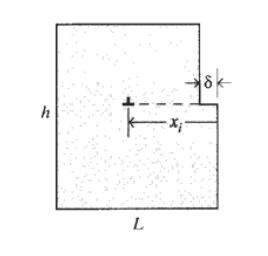
The plastic flow rate is related directly to dislocation velocity, which can be visualized by considering a section of material of height \(h\) and width \(L\) as shown in Figure 16. A single dislocation, having traveled in the width direction for the full distance \(L\) will produce a transverse deformation of \(\delta_i = \bar{b}\). If the dislocation has propagated through the crystal only a fraction \(x_i/L\) of the width, the deformation can be reduced by this same fraction: \(\delta_i = \bar{b}(x_i/L)\). The total deformation in the crystal is then the sum of the deformations contributed by each dislocation:
\(\delta = \sum_i \delta_i = \sum_i \bar{b} (x_i/L)\)
The shear strain is the ratio of the transverse deformation to the height over which it is distributed:
\(\gamma = \dfrac{\delta}{h} = \dfrac{\bar{b}}{Lh} \sum_i x_i\)
The value \(\sum_i x_i\) can be replaced by the quantity \(N_{\bar{x}}\), where \(N\) is the number of dislocations in the crystal segment and \(\bar{x}\) is the average propagation distance. We can then write
\(\gamma = \rho \bar{b}\bar{x}\)
where \(\rho = N/Lh\) is the dislocation density in the crystal. The shear strain rate \(\dot{\gamma}\) is then obtained by differentiation:
\[\dot{\gamma} = \rho \bar{b} v\]
where \(v = \dot{\bar{x}}\) is the average dislocation velocity. Hence the creep rate scales directly with the dislocation velocity.
To investigate the temperature and stress dependence of this velocity, we consider rate at which dislocations can overcome obstacles to be yet another example of a thermally activated, stress aided rate process and write an Eyring equation for the creep rate:
where \(V^*\) is an apparent activation volume. The second term here indicates that the activation barrier for motion in the direction of stress is augmented by the stress, and diminished for motions in the opposite direction. When we discussed yielding the stress was sufficiently high that motion in the direction opposing flow could be neglected. Here we are interested in creep taking place at relatively low stresses and at high temperature, so that reverse flow can be appreciable. Factoring,
Since \(\sigma V^* \ll RT\), we can neglect quadratic and higher order terms in the series expansion \(e^x = 1 + x + (x^2/2!) + (x^3/3!) + \cdots \) to give
\(\dot{\epsilon} = A (\dfrac{\sigma V^*}{RT}) \exp \dfrac{-(E_d^*)}{RT}\)
If now we neglect the temperature dependence in the preexponential factor in comparison with the much stronger temperature dependence of the exponential itself, this model predicts a creep rate in agreement with the Weertman-Dorn equation with \(m = 1\).
Creep by dislocation glide occurs over the full range of temperatures from absolute zero to the melting temperature, although the specific equation developed above contains approximations valid only at higher temperature. The stresses needed to drive dislocation glide are on the order of a tenth the theoretical shear strength of \(G/10\). At lower stresses the creep rate is lower, and becomes limited by the rate at which dislocations can climb over obstacles by vacancy diffusion. This is hinted at in the similarity of the activation energies for creep and self diffusion as shown in Figure 17. (Note that these values also correlate with the tightness of the bond energy functions, as discussed in Module 1; diffusion is impeded in more tightly-bonded lattices.) Vacancy diffusion is another stress-aided thermally activated rate process, again leading to models in agreement with the Weertman-Dorn equation.

Exercise \(\PageIndex{1}\)
The yield stresses \(\sigma_Y\) have been measured using steel and aluminum specimens of various grain sizes, as follows:
| Material | d, \(\mu\) | \(\sigma_Y, MPa\) |
|---|---|---|
| steel | 60.5 | 160 |
| 136 | 130 | |
| aluminum | 11.1 | 235 |
| 100 | 225 |
- Determine the coefficients \(\sigma_0\) and \(k_Y\) in the Hall-Petch relation (Equation 6.2.7) for these two materials.
- Determine the yield stress in each material for a grain size of \(d = 30\mu\).


