11.3: Incompressibility

Numerous experiments performed over the past 100% have shown that metals are practically incompressible in the plastic range. Let’s explore the consequences of this physical fact in the case of one-dimensional case. Denote the gauge length of the prismatic bar by \(l\) and its cross-sectional area by \(A\). The current volume of the gauge section is \(V = Al\). Incompressibility means that the volume must be unchanged or \(dV = 0\).

\[dV = d(Al) = dAl + Adl = 0 \label{11.3.1}\]

From Equation \ref{11.3.1} we infer that the strain increment \(d\epsilon\) can be calculated either by tracking down the gauge length or the cross-sectional area

\[d\epsilon = \frac{dl}{l} = − \frac{dA}{A} \label{eq0}\]

Integrating the first part of Equation \ref{eq0}

\[\epsilon = \ln l + C_1 \]

The integration constant is obtained by requiring that the strain vanishes when the length \(l\) is equal to the gauge initial, reference length \(l_o\), which gives \(C = − \ln l_o\). Thus

\[\epsilon = \ln \frac{l}{l_o} \label{eq1}\]

which is the logarithmic definition of strain, introduced in Chapter 1. Similarly, integrating the second part of Equation \ref{eq0} with the initial condition at \(A = A_o\), \(\epsilon = 0\), one gets

\[\epsilon = \ln \frac{A_o}{A} \label{eq2}\]

In tension \(l > l_o\) or \(A < A_o\), so both Equations \ref{eq1} and \ref{eq2} gives the positive strain. In compression the strain is negative. The same is true for strain increments \(d\epsilon\) or strain rates

\[\dot{\epsilon} = \frac{\dot{l}}{l} \quad \text{ or } \quad \dot{\epsilon} = − \frac{\dot{A}}{A} \]

From the above analysis follows a simple extension of the plastic incompressibility condition into the 3-D case. Consider an infinitesimal volume element \(V = x_1x_2x_3\), Figure (\(\PageIndex{1}\))

Figure \(\PageIndex{1}\): Undeformed and deformed 1-D and 3-D volume elements.

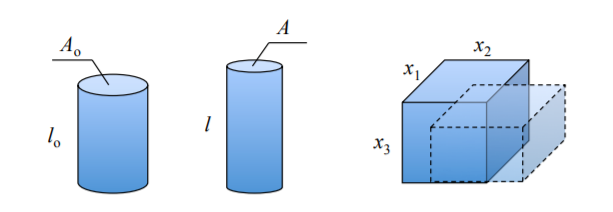
The plastic incompressibility requires that

\[dV = d(x_1x_2x_3) = dx_1(x_2x_3) + x_1d(x_2x_3) \\ = dx_1x_2x_3 + x_1dx_2x_3 + x_1x_2dx_3 \]

Dividing both sides of the above equation by the volume, one gets

\[\frac{dx_1}{x_1} + \frac{dx_2}{x_2} + \frac{dx_3}{x_3} = 0 \]

or

\[d\epsilon_{11} + d\epsilon_{22} + d\epsilon_{33} = 0, \quad d\epsilon_{kk} = 0 \nonumber \]

Noting that \(d\epsilon_{11} = \frac{\partial \epsilon_{11}}{\partial t} dt = \dot{\epsilon}_{11}dt\), an alternative form of the incompressibility condition is

\[\dot{\epsilon}_{11} + \dot{\epsilon}_{22} + \dot{\epsilon}_{33} = 0, \quad \dot{\epsilon}_{kk} = 0 \]

The sum of the diagonal components of the strain rate tensor must vanish to ensure incompressibility. It follows from the flow rule (to be formulated later) that in uniaxial tension in \(x_1\) direction the components \(\dot{\epsilon}_{22} = \dot{\epsilon}_{33}\). Therefore \(\dot{\epsilon}_{11} + 2\dot{\epsilon}_{22} = 0\) or \(\dot{\epsilon}_{11} + 2\dot{\epsilon}_{33} = 0\). Finally we obtain

\[\dot{\epsilon}_{22} = −0.5\dot{\epsilon}_{11}, \quad \dot{\epsilon}_{33} = −0.5\dot{\epsilon}_{11} \]

The coefficient 0.5 can be interpreted as the Poisson ratio

\[\nu = − \frac{\dot{\epsilon}_{22}}{\dot{\epsilon}_{11}} = − \frac{\dot{\epsilon}_{33}}{\dot{\epsilon}_{11}} = 0.5 \]

We can conclude that plastic incompressibility requires that the Poisson ratio be equal to \(1/2\), which is different from the elastic Poisson ratio, equal \(\tilde 0.3\) for metals. Many other materials such as rubber, polymers and water are incompressible.