12.3: Design for Nominal Performance

Last updated
Save as PDF

Page ID: 47295

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Performance requirements of a feedback controller, using the nominal plant model, can be cast in terms of the Nyquist plot. Since the sensitivity function maps reference input \(r(s)\) to tracking error \(e(s)\), we know that \(|S(s)|\) should be small at low frequencies. For example,

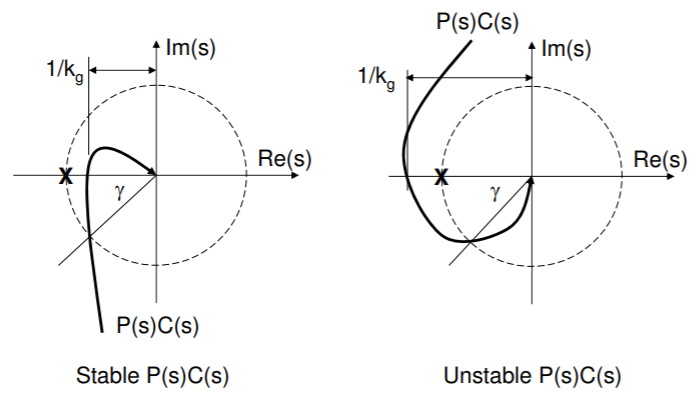
Figure comparing two graphs, showing how the value of the gain margin varies between a stable and an unstable OL transfer function. — Figure \(\PageIndex{1}\): comparison of graphs demonstrates how differences in the value of the gain margin (\(k_g\)) determine the stability or unstability of the OL transfer function, as explained in the previous section.

if one-percent tracking is to be maintained for all frequencies below \(\omega = \gamma\), then \(|S(s)| = < 0.01, \, \forall \omega < \gamma.\) This can be formalized by writing

\[ |W_1(s) S(s)| < 1, \]

where \(W_1(s)\) is a stable weighting function of frequency. To force \(S(s)\) to be small at low \(\omega\), \(W_1 (s)\) should be large in the same range. The requirement \(|W_1(s) S(s)| < 1\) is equivalent to \(|W_1(s)| < |1 + P(s)C(s)|\), and this latter condition can be interpreted as: The loci of \(P(s)C(s)\) must stay outside the disk of radius \(W_1(s)\), which is to be centered on the critical point \((-1 + 0j)\). The disk is to be quite large, possibly infinitely large, at the lower frequencies.