Solving the Ultraviolet Catastrophe
- Page ID
- 319
Introduction
This is a very interesting story which first time lead people to believe that energies (associated with waves) are quantized rather than continuous. It all started with Black Body radiation when scientist attempted to explain the curve of frequency (or wavelength) vs intensity. Max Planck was first to explain the behavior in 1900\(^{[3]}\), but no one accepted it; as there is no explanation for assuming energy corresponding to particular wavelength quantized rather than continuous. Instead Rayleigh-Jeans law which was proposed after Plack's law was accepted though it failed at low value of wavelength as it was based on the equipartition theorem of classical statistical mechanics. Planck's law was accepted only when Einstein applied quantization of energy to explain specific heat of materials at low temperature in 1905. The term "ultraviolet catastrophe" was first used in 1911 by Paul Ehrenfest\(^{[1]}\).
Black Body Radiation
Black Body
A black body is an idealized object which absorbs and emits all frequencies. It refers to an object or system which absorbs all radiation incident upon it and re-radiates energy which is characteristic of this radiating system only, not dependent upon the type of radiation which is incident upon it. The radiated energy can be considered to be produced by standing wave or resonant modes of the cavity which is radiating.
Explaining Black Body Radiation
Classical physics can be used to derive an equation which describes the intensity of blackbody radiation as a function of frequency for a fixed temperature the result is known as the Rayleigh-Jeans law\(^{[2]}\). Although the Rayleigh-Jeans law works for higher wavelengths \(\lambda\), it diverges as \(\lambda\) become low in value; this divergence for high frequencies is called the ultraviolet catastrophe.
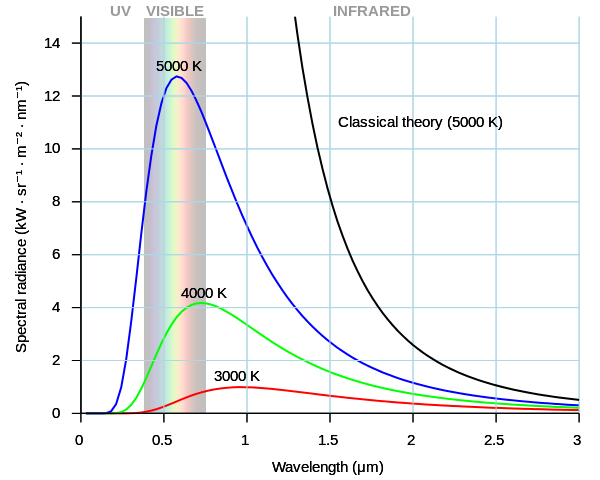
Figure \(\PageIndex{1}\) The ultraviolet catastrophe is the error at short wavelengths in the Rayleigh–Jeans law (depicted as "classical theory" in the graph) for the energy emitted by an ideal black-body. The error, much more pronounced for short wavelengths, is the difference between the black curve (as classically predicted by the Rayleigh–Jeans law) and the blue curve (the measured curve as predicted by Planck's law). from Wikipedia.
The radiated energy can be considered to be produced by standing wave or resonant modes of the cavity which is radiating.
A single standing wave in stationary medium. The red dots represent the wave nodes. from Wikipedia.
Source: Boundless. “Standing Waves and Resonance.” Boundless Physics. Boundless, 21 Jul. 2015. Retrieved 25 Aug. 2015 from www.boundless.com/physics/te...ance-445-6334/
Max Planck explained the blackbody radiation in 1900 by assuming that the energies of the oscillations of electrons which gave rise to the radiation are proportional to integral multiples of the frequency i.e.
\[ \begin{align} E=\dfrac{hc}{\lambda} \end{align} \label{1}\]
Rayleigh-Jeans Law derivation \(^{[4]}\)
Electromagnetic Waves in a Cubical Cavity
Electromagnetic standing waves in a cavity at equilibrium with its surroundings cannot take just any path. They must satisfy the wave equation in three dimensions:
\[ \begin{align} n_{1}^{2} + n_{2}^{2} + n_{3}^{2}= \dfrac{4L^{2}}{\lambda} \end{align} \label{2}\]
where \(L\) is the length of the cavity, \(\lambda\) is wavelength and \(n_{1}\) \(n_{2}\) and \(n_{3}\) are number of waves in x, y and z directions.
Number of modes in the cavity
We need to evaluate the number of modes which can meet this condition, which amounts to counting all the possible combinations of the integer n values. An approximation can be made by treating the number of combinations as the volume of a three-dimensional grid of the values of n, an "n-space". Using the relationship for the volume of a sphere, with the n values specifying the coordinates along three "n" axes, gives
Volume of n's
\[ \begin{align} =\dfrac{4\pi}{3}(n_{1}^{2} + n_{2}^{2} + n_{3}^{2})^{3/2} \end{align} \label{3}\]
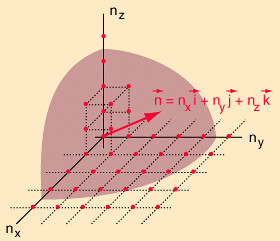
Figure \(\PageIndex{2}\) The Rayleigh scheme for counting modes.
In using a sphere, we have used both positive and negative values of n, whereas the wave equation solution uses only positive definite values. Therefore we must take 1/8 th of the volume above. Another technical problem is that you can have waves polarized in two perpendicular planes, so we must multiply by two to account for that. Then the volume can be taken to be a measure of the number of modes, becoming a very good approximation when the size of the cavity is much greater than the wavelength as in the case of electromagnetic waves in finite cavity. Using the relation obtained for the values of n, this becomes
Number of modes N
\[ \begin{align} =\dfrac{\pi}{3}(n_{1}^{2} + n_{2}^{2} + n_{3}^{2})^{3/2}=\dfrac{8\pi L^{3}}{3\lambda^{3}} \end{align} \label{4}\]
Number of modes per unit wavelength
This may be obtained by taking the derivative of the number of modes with respect to wavelength.
\[ \begin{align} \dfrac{dN}{d\lambda}= \dfrac{d}{d\lambda} \left[\dfrac{8\pi L^{3}}{3\lambda^{3}} \right]= - \dfrac{8\pi L^{3}}{\lambda^{4}} \end{align} \label{5}\]
The negative sign here reveals that the number of modes decreases with increasing wavelength. Now to get the number of modes per unit volume per unit wavelength, we can simply divide by the volume of the cubical cavity. Dividing above term by \(L^{3}\) on each side gives.
\[ \begin{align} -\dfrac{dN}{d\lambda L^{3}}= \dfrac{8\pi}{\lambda^{4}} \end{align} \label{6}\]
Energy per unit volume
Assigning energy to the electromagnetic standing waves in a cavity draws on the principle of equipartition of energy. Each standing wave mode will have average energy kT where k is Boltzmann's constant and T the temperature in Kelvin. Letting U represent the energy density:
\[ \begin{align} \dfrac{dU}{d\lambda}=\dfrac{dE}{d\lambda L^{3}}=-kT\dfrac{dN}{L^{3} d\lambda}=\dfrac{8\pi kT}{\lambda^{4}} \end{align} \label{7}\]
According to above formula if (\lambda\) tends to zero i.e. corresponding every per unit volume would be infinity. But this is not the case. Energy per unit volume peaks at some value and then starts decreasing as shown in Figure \(\PageIndex{1}\).
Planck's solution
From the assumption that the standing electromagnetic modes in a cavity were quantized in energy with the energy equal to Planck's constant times the frequency that for wavelength \(\lambda\): \(E=\dfrac{hc}{\lambda}\), Planck derived a radiation formula that the average energy per "mode" or "quantum" is the energy of the quantum times the probability that it will be occupied (the Einstein-Bose distribution function) i.e.
\[\begin{align} \langle E \rangle=\dfrac{hc}{\lambda(e^{\frac{hc}{\lambda kT}}-1)} \end{align} \label{8}\]
Now taking \(\langle E \rangle\) as energy per unit mode per unit volume. We get energy per unit volume as
\[ \begin{align} \dfrac{dU}{d\lambda}=\dfrac{8\pi hc}{\lambda^{5} (e^{\frac{hc}{\lambda kT}}-1)} \end{align} \label{9}\]
- As \(\lambda \Rightarrow 0\): \[ e^{\frac{hc}{\lambda kT}} \Rightarrow \infty\] Hence compensate \(\lambda\) tends to infinity and hence compensate \(\lamda\) tending to zero in denominator. And hence energy per unit volume does not blow to infinity at very low value of \(\lambda\).
- As \(\lambda \Rightarrow \infty\): \[ e^{\frac{hc}{\lambda kT}}-1 \Rightarrow \dfrac{hc}{\lambda kT} .\] Thus energy per unit volume reduces to \(\dfrac{8\pi kT}{\lambda^4}\) same as predicted by Rayleigh-Jeans law.
Aftermath
People started accepting the fact that energy is quantized and not only energy but angular momentum as in case of Bohr's assumption in Hydrogen atom. This lead to whole new era of physics to understand this quantization. In order to deal with new found quantization a whole new mechanics evolved which is completely different form Newtonian Mechanics and now popularly called Quantum Mechanics.
References
- en.Wikipedia.org/wiki/Ultraviolet_catastrophe
- en.Wikipedia.org/wiki/Rayleigh-Jeans_law
- its-catastrophe.net/
- http://hyperphysics.phy-astr.gsu.edu
- http://electrons.wikidot.com/experimental-background-of-quantum-mechanics
Contributors and Attributions
ContribMSE5317

